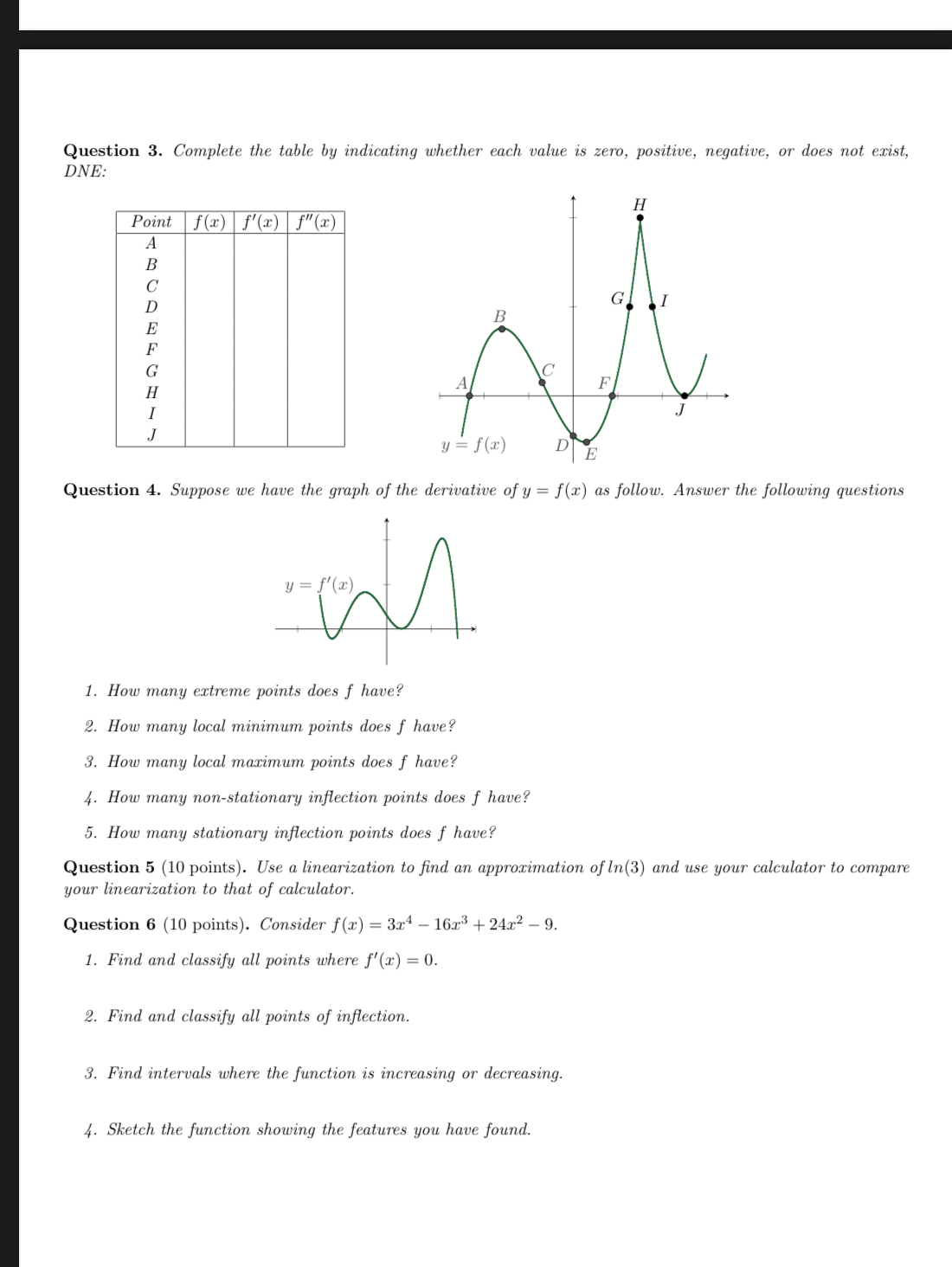
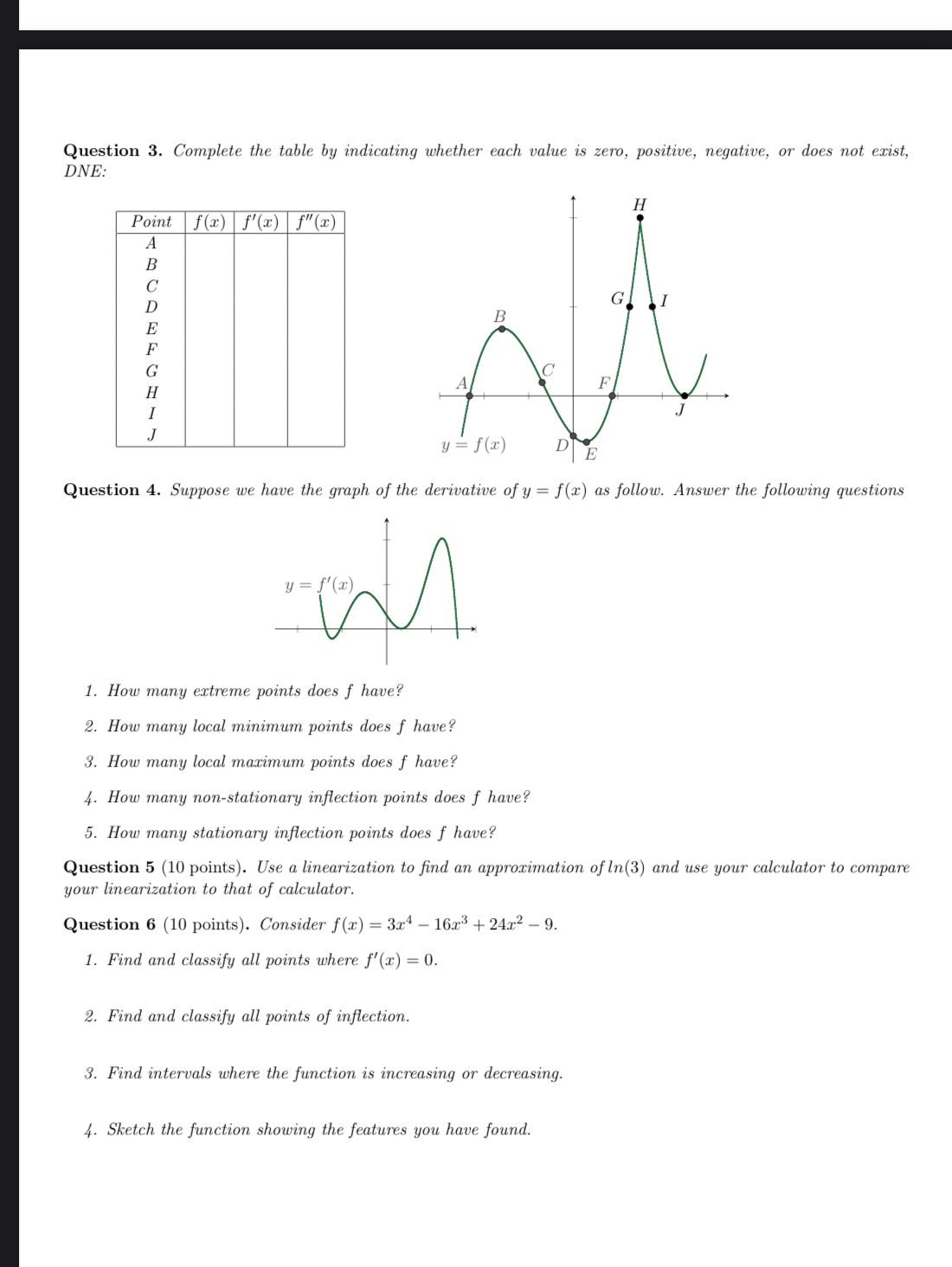
Question 3. Complete the table by indicating whether each value is zero, positive, negative, or does not exist, DNE: Point f(x) f'(x) f"(x) H A B C GI B C F = f(x) E Question 4. Suppose we have the graph of the derivative of y = f(x) as follow. Answer the following questions y = f(x) 1. How many extreme points does f have? 2. How many local minimum points does f have? 3. How many local maximum points does f have? 4. How many non-stationary inflection points does f have? 5. How many stationary inflection points does f have? Question 5 (10 points). Use a linearization to find an approximation of In(3) and use your calculator to compare your linearization to that of calculator. Question 6 (10 points). Consider f(x) = 3x4 - 1613 + 24x2 -9. 1. Find and classify all points where f'(x) = 0. 2. Find and classify all points of inflection. 3. Find intervals where the function is increasing or decreasing. 4. Sketch the function showing the features you have found