QUESTION $3($Discrete$-$variable Optimization, Unconstrained$).$ Tool to use: Knapsack or binary

programming.

As most sewer pipes in developed countries approach the end of their service lives, there is increasing

danger of pipe failures, leakages, and violent explosions due to methane gas accumulations. Therefore,

there exists an urgent need to carry out rehabilitation in order to extend sewer pipe service lives.

However, most cities are finding that budgets are limited and therefore not all sewer pipes can be

rehabilitated with available budgets.

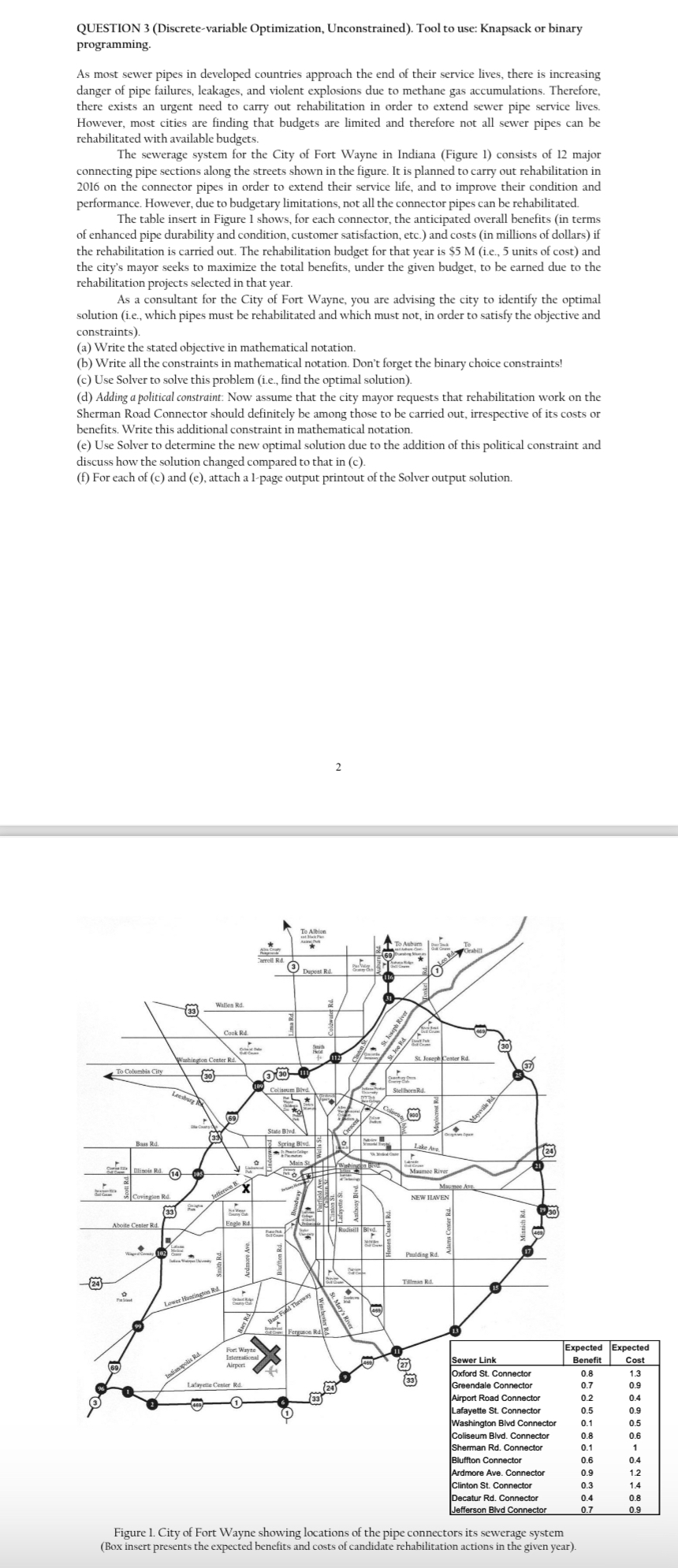
The sewerage system for the City of Fort Wayne in Indiana $($Figure $1)$ consists of $12$ major

connecting pipe sections along the streets shown in the figure. It is planned to carry out rehabilitation in

$2016$ on the connector pipes in order to extend their service life, and to improve their condition and

performance. However, due to budgetary limitations$,$ not all the connector pipes can be rehabilitated.

The table insert in Figure $1$ shows, for each connector, the anticipated overall benefits $($in terms

of enhanced pipe durability and condition, customer satisfaction, etc.$)$ and costs $($in millions of dollars$)$ if

the rehabilitation is carried out. The rehabilitation budget for that year is $$5M($i$.$e$.,5$ units of cost$)$ and

the city's mayor seeks to maximize the total benefits, under the given budget, to be earned due to the

rehabilitation projects selected in that year.

As a consultant for the City of Fort Wayne, you are advising the city to identify the optimal

solution $($i$.$e$.,$ which pipes must be rehabilitated and which must not, in order to satisfy the objective and

constraints$).$

$($a$)$ Write the stated objective in mathematical notation.

$($b$)$ Write all the constraints in mathematical notation. Don't forget the binary choice constraints!

$($c$)$ Use Solver to solve this problem $($i$.$e$.,$ find the optimal solution$).$

$($d$)$ Adding a political constraint: Now assume that the city mayor requests that rehabilitation work on the

Sherman Road Connector should definitely be among those to be carried out, irrespective of its costs or

benefits. Write this additional constraint in mathematical notation.

$($e$)$ Use Solver to determine the new optimal solution due to the addition of this political constraint and

discuss how the solution changed compared to that in $($c$)$

$($f$)$ For each of $($c$)$ and $($e$),$ attach a $1-$page output printout of the Solver output solution

Figure $1.$ City of Fort Wayne showing locations of the pipe connectors its sewerage system

$($Box insert presents the expected benefits and costs of candidate rehabilitation actions in the given year$).$