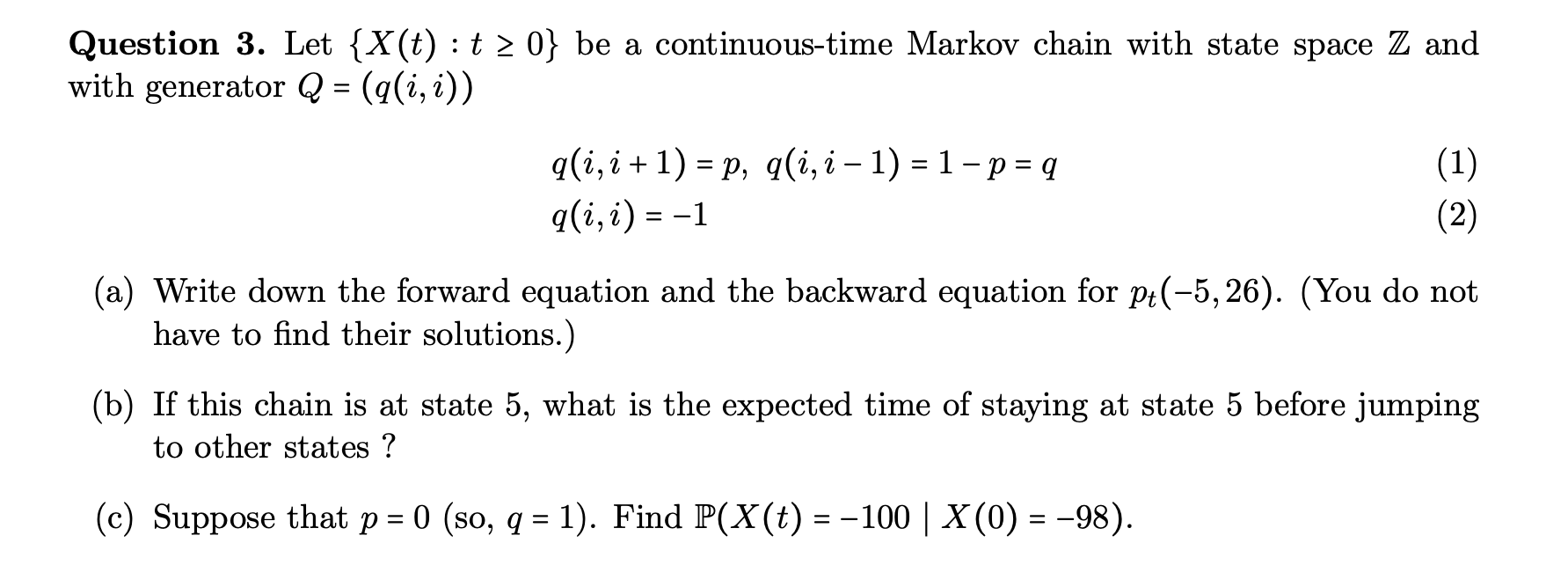
: Question 3. Let {X(t):t > 0} be a continuous-time Markov chain with state space Z and with generator Q = (q(i, i)) = = q(i,i + 1) = p, q(i,i-1) = 1 - p = 9 ali, i) = -1 (1) (2) = (a) Write down the forward equation and the backward equation for pt(-5, 26). (You do not have to find their solutions.) (b) If this chain is at state 5, what is the expected time of staying at state 5 before jumping to other states ? (c) Suppose that p = 0 (so, q = 1). Find P(X(t) = -100 | X(0) = -98). = = = = : Question 3. Let {X(t):t > 0} be a continuous-time Markov chain with state space Z and with generator Q = (q(i, i)) = = q(i,i + 1) = p, q(i,i-1) = 1 - p = 9 ali, i) = -1 (1) (2) = (a) Write down the forward equation and the backward equation for pt(-5, 26). (You do not have to find their solutions.) (b) If this chain is at state 5, what is the expected time of staying at state 5 before jumping to other states ? (c) Suppose that p = 0 (so, q = 1). Find P(X(t) = -100 | X(0) = -98). = = = =