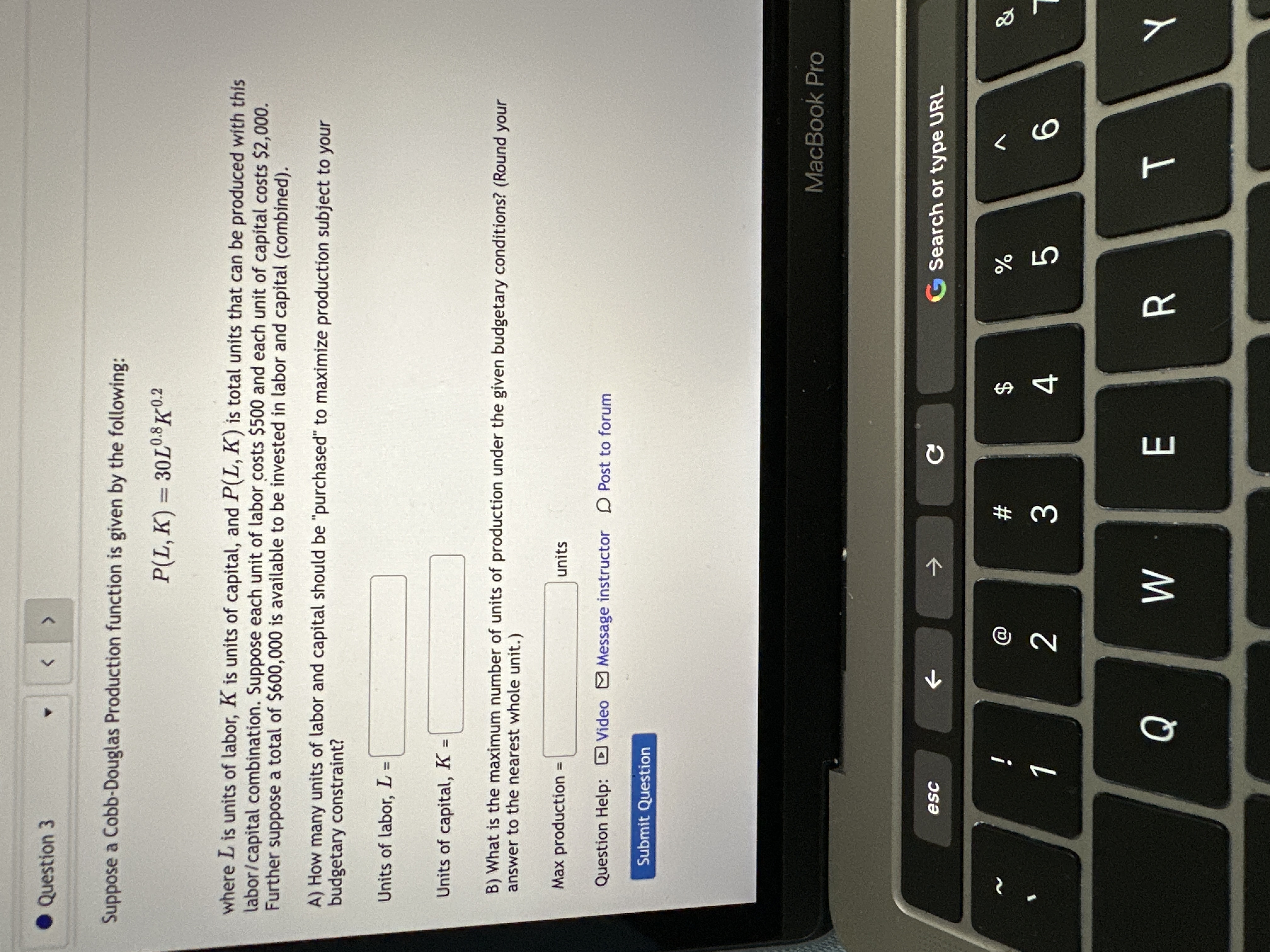
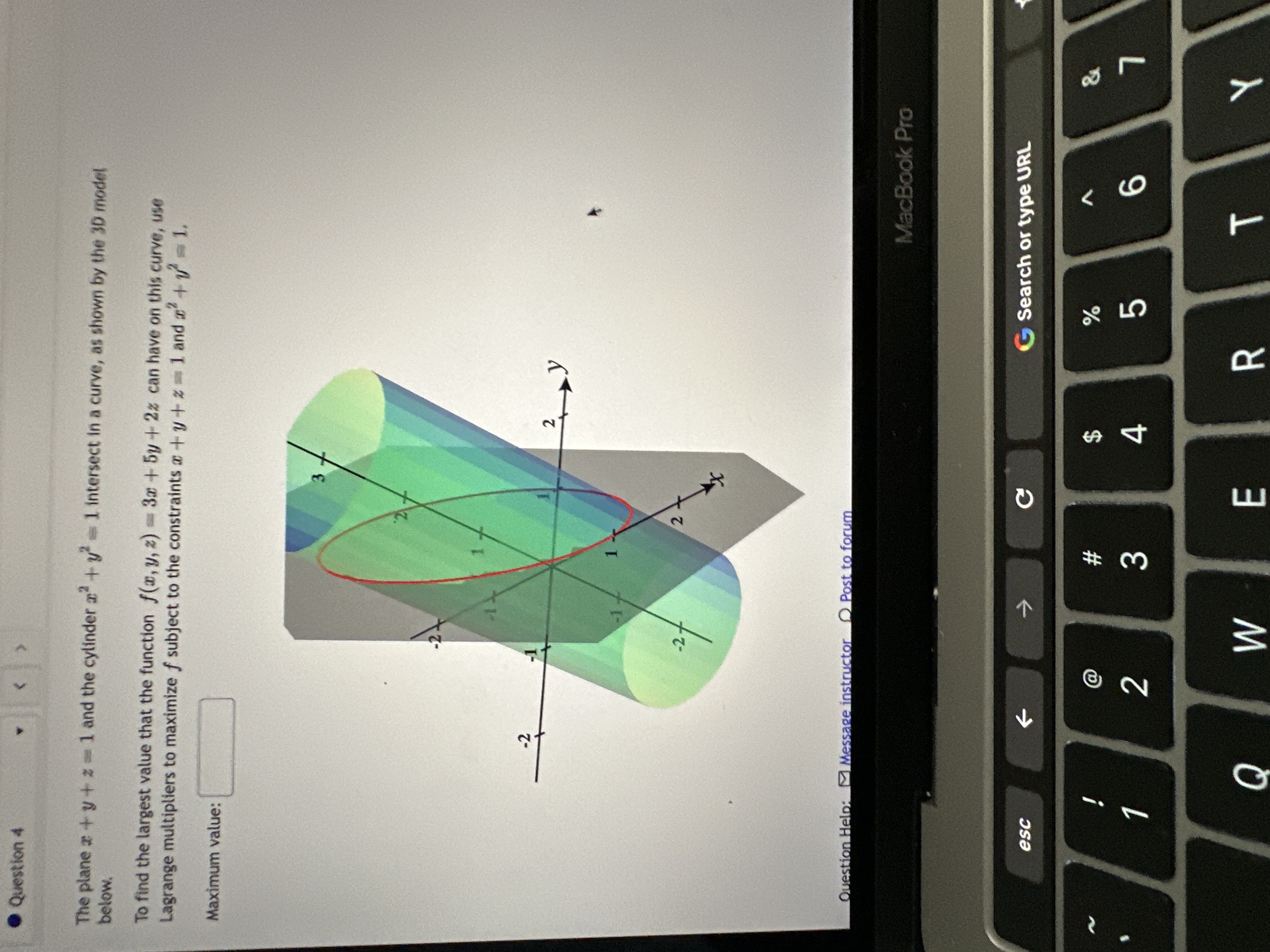
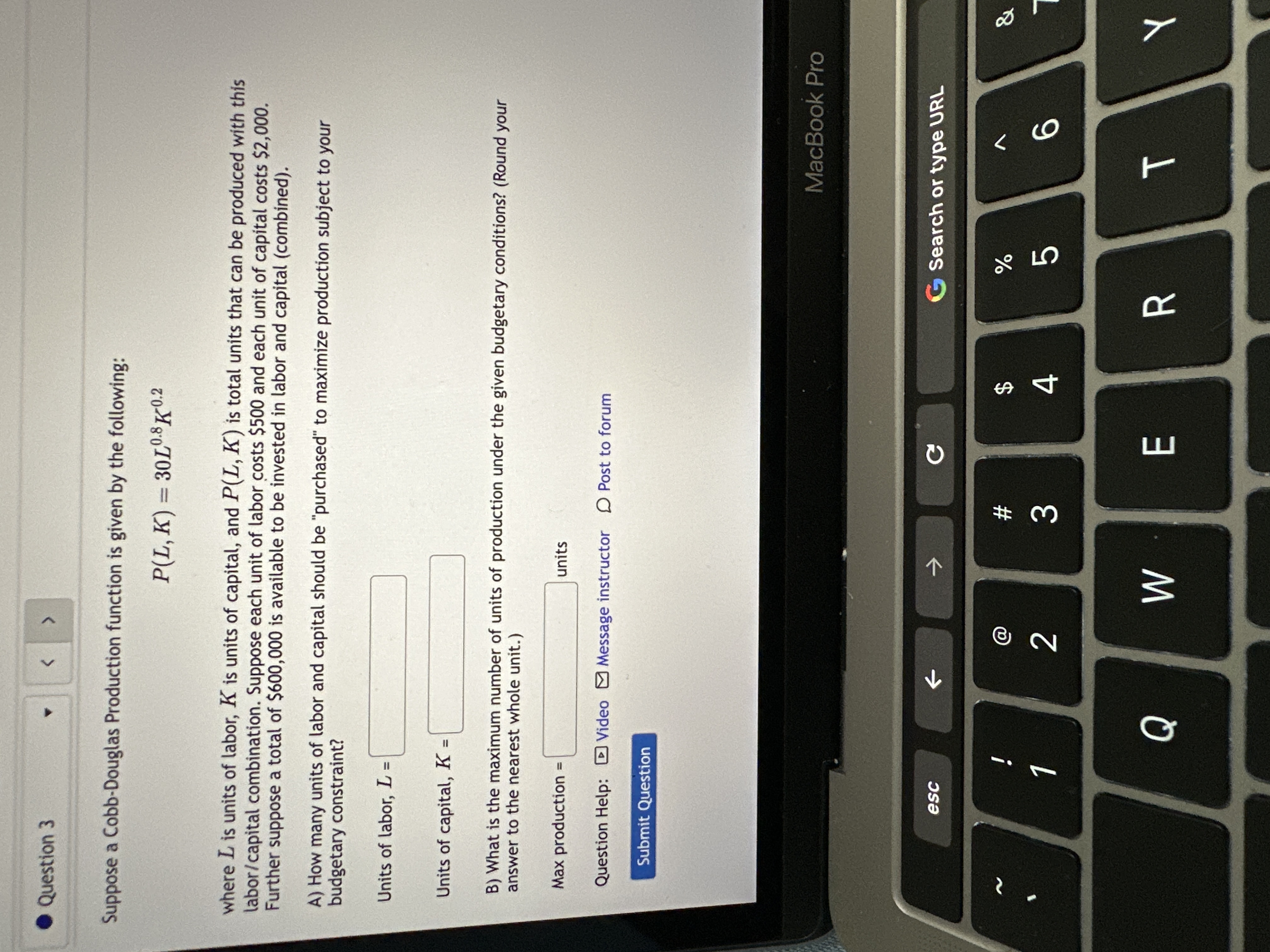
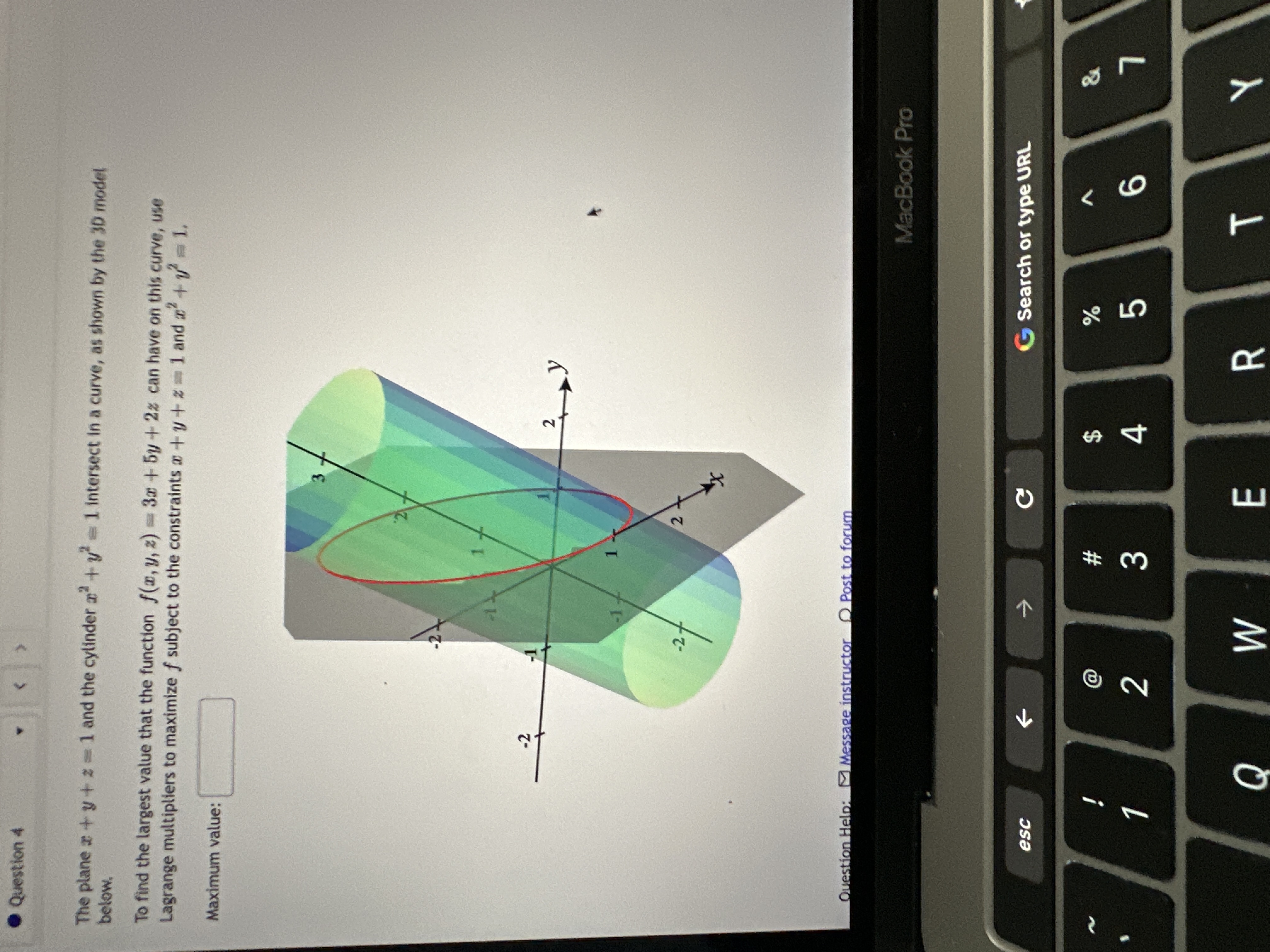
Question 3 Suppose a Cobb-Douglas Production function is given by the following: P(L, K) = 3010.8 1 0.2 where L is units of labor, K is units of capital, and P(L, K) is total units that can be produced with this labor/capital combination. Suppose each unit of labor costs $500 and each unit of capital costs $2,000. Further suppose a total of $600,000 is available to be invested in labor and capital (combined). A) How many units of labor and capital should be "purchased" to maximize production subject to your budgetary constraint? Units of labor, L = Units of capital, K = B) What is the maximum number of units of production under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production = units Question Help: Video Message instructor D Post to forum Submit Question MacBook Pro esc C G Search or type URL EA % & W # 2 4 5 Q W m R T Y. Question 4 The plane a + y + 2 - 1 and the cylinder a + y' - 1 intersect in a curve, as shown by the 3D model below. To find the largest value that the function f(x, y, z) = 3x + 5y + 2z can have on this curve, use Lagrange multipliers to maximize f subject to the constraints a + y + z = 1 and + 1 = 1, Maximum value: -2 2 -27 Question Help: Message instructor O Post to forum MacBook Pro esc C G Search or type URL @ % N 3 4 5 Q W E R T Y