Question 3

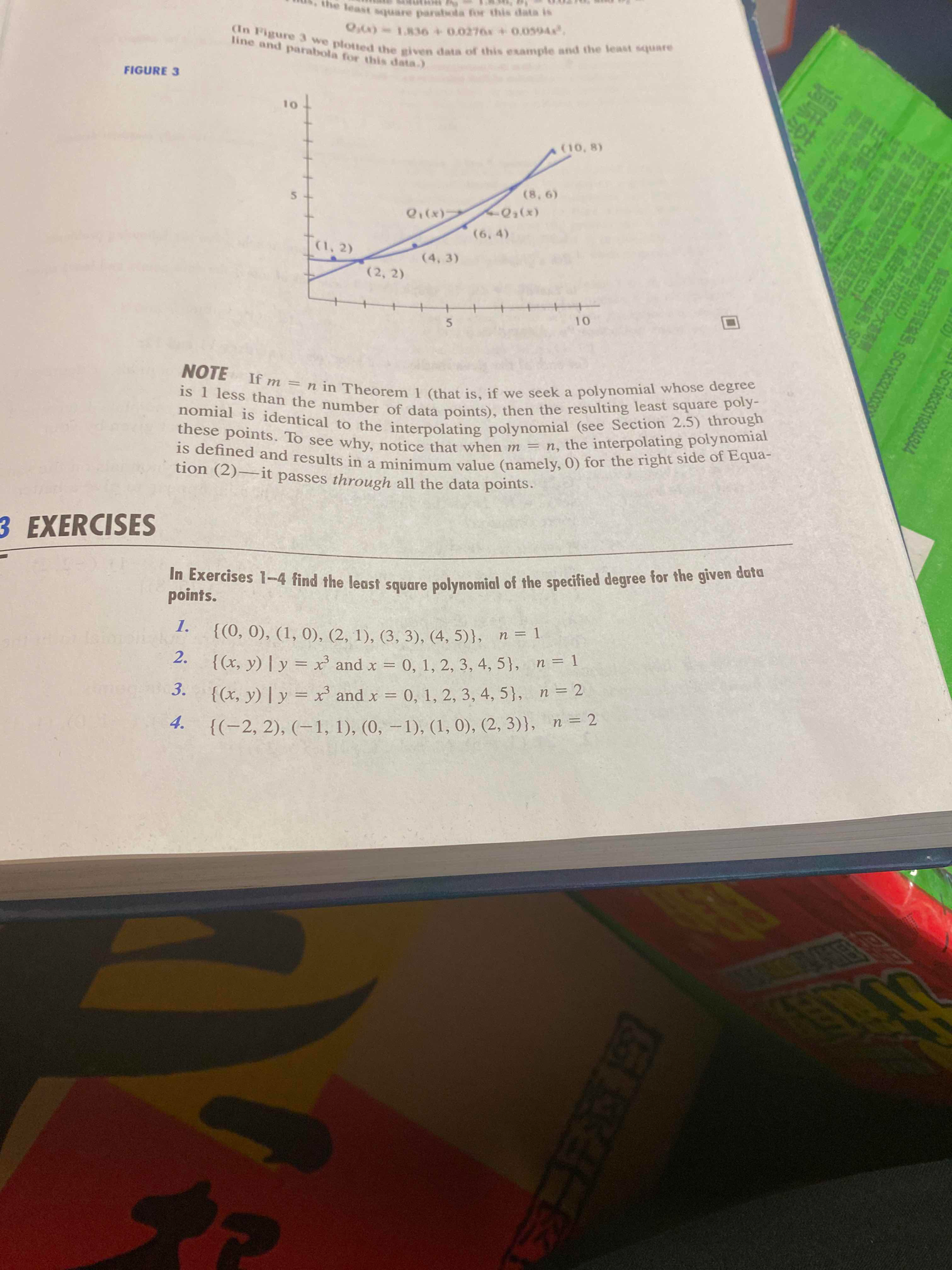
the least square parabola for this data is Q:() - 1.830 + 0.0276 + 0.0594. (In Figure 3 we plotted the given d line and parabola for this data.) given data of this example and the least square FIGURE 3 10 (10, 8) S (8, 6) 10, ( x ) (1. 2) (6. 4) (2. 2) (4, 3) NOTE If m = n in Theorem 1 (that is, if we seek a polynomial whose degree is 1 less than the number of data points), then the resulting least square poly- nomial is identical to the i the interpolating polynomial (see Section 2.5) through these points. To see why, notice that when m = n, the interpolating polynomial is defined and results in a minimum value (namely, 0) for the right side of Equa- tion (2)-it passes through all the data points. EXERCISES In Exercises 1-4 find the least square polynomial of the specified degree for the given data points. 1. { (0, 0), (1, 0), (2, 1), (3, 3), (4, 5) }, n = 1 2. { (x, y) ly = x3 and x = 0, 1, 2, 3, 4, 5}, in = 1 3. { (x, y) ly = x3 and x = 0, 1, 2, 3, 4, 5}, n = 2 4. { ( - 2, 2 ), ( - 1, 1), (0, -1), (1, 0 ), (2, 3 ) } , n = 2