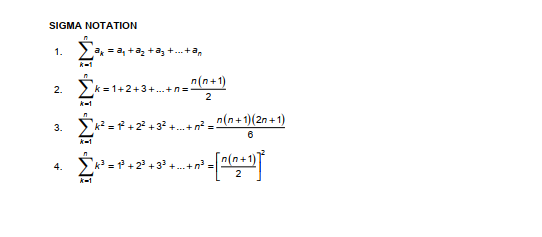
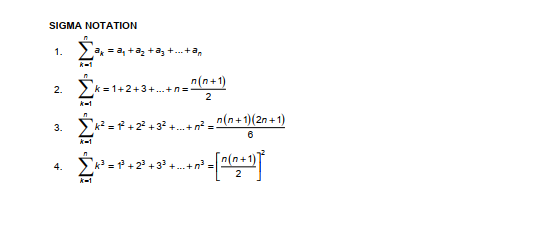
QUESTION 4 100 100 100 a) Given that > ax = 20 and 1DK = -10. Compute (2ak + 5bk) K=1 *=1 K=1 (3 marks) b) Evaluate i) (sin (4x + 12 ) +(5-*)5) dx (3 marks) i) [2wx + 3X dx (4 marks) m ) [ f(x ) dx if f(x ) = [sec2 3x ; x>1 le3x ; xs1 (5 marks) iv) 4x dx 1 (4+ 2x2 ) (6 marks) cos 2x c) Given that F(x) = | (512 +5sint +t) at. Find F'(0) by using the first part of Fundamental Theorem of Calculus (FTC1). [g(x) Hint: [ f(t ) at = f (g(x)) 9'(x) (5 marks)APPENDIX RULES OF DIFFERENTIATION 1. Product rule "(f (x)g(x) ) = g(x)f'(x ) +f(x)g'(x) 2. Quotient rule d (f(x) _ g(x) f(x )-f(x) g'( x) ax g(x)) (g(x)) 3. Power rule d x ( F ( x ) " = [f(x] f( x ) 4. Chain rule " f(g(x)) = f(g(x)) g'(x) TABLE OF INTEGRALS (ax +b)"+1 ) 1. (ax + b )" dx= a(n + 1) -Inlax + b/ +C : n=1 2 . - dx = In/ x / + C 3. sin axd x = - -cos ax + C a 4. cos axd x = - sin ax + C 5. sec' axdx = -tan ax + C 6. csch axdx = --cot ax + C a DEFINITION OF DIFFERENTIATION F(x) = lim f( x+h)-f(x) 1-+0 h LINEAR APPROXIMATION f(x) =f(x) +f'(x) (x -*0) THE SQUEEZING THEOREM SIn A 1. lim 2 lim 1-005 X_ = 0 XSIGMA NOTATION 1. ata ta, tag +...+a, n(n+1) 2. k =1+2+3+...+0= 2 k-1 n n(n + 1) (20 + 1) 3. k-1 n n(n + 1) 12 4. 43=1+2'+3 +.. . +n'= 2