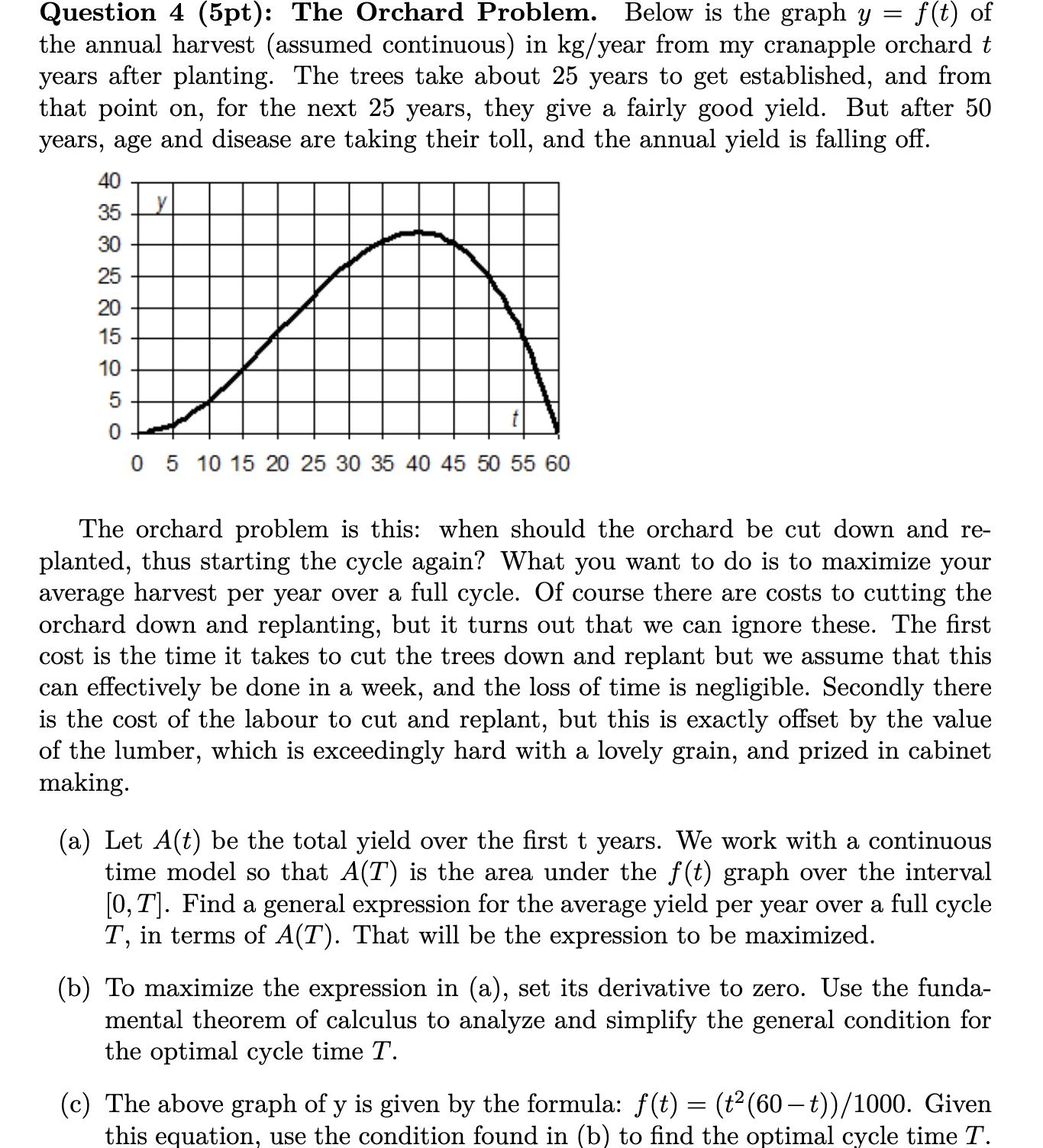
Question $4(5$pt$)$: The Orchard Problem. Below is the graph $\backslash ($ y$=$f$($t$)\backslash )$ of the annual harvest $($assumed continuous$)$ in $\backslash (\backslash$mathrm$\{$kg$\}/\backslash )$ year from my cranapple orchard $\backslash ($ t $\backslash )$ years after planting. The trees take about $25$ years to get established, and from that point on$,$ for the next $25$ years, they give a fairly good yield. But after $50$ years, age and disease are taking their toll, and the annual yield is falling off.

The orchard problem is this: when should the orchard be cut down and replanted, thus starting the cycle again? What you want to do is to maximize your average harvest per year over a full cycle. Of course there are costs to cutting the orchard down and replanting, but it turns out that we can ignore these. The first cost is the time it takes to cut the trees down and replant but we assume that this can effectively be done in a week, and the loss of time is negligible. Secondly there is the cost of the labour to cut and replant, but this is exactly offset by the value of the lumber, which is exceedingly hard with a lovely grain, and prized in cabinet making.

$($a$)$ Let $\backslash ($ A$($t$)\backslash )$ be the total yield over the first t years. We work with a continuous time model so that $\backslash ($ A$($T$)\backslash )$ is the area under the $\backslash ($ f$($t$)\backslash )$ graph over the interval $\backslash ([0,$ T$]\backslash ).$ Find a general expression for the average yield per year over a full cycle $\backslash ($ T $\backslash ),$ in terms of $\backslash ($ A$($T$)\backslash ).$ That will be the expression to be maximized.

$($b$)$ To maximize the expression in $($a$),$ set its derivative to zero. Use the fundamental theorem of calculus to analyze and simplify the general condition for the optimal cycle time $\backslash ($ T $\backslash ).$

$($c$)$ The above graph of y is given by the formula: $\backslash ($ f$($t$)=\backslash$left$($t$^\{2\}(60-$t$)\backslash$right$)/1000\backslash ).$ Given this equation, use the condition found in $($b$)$ to find the optimal cycle time $\backslash ($ T $\backslash ).$