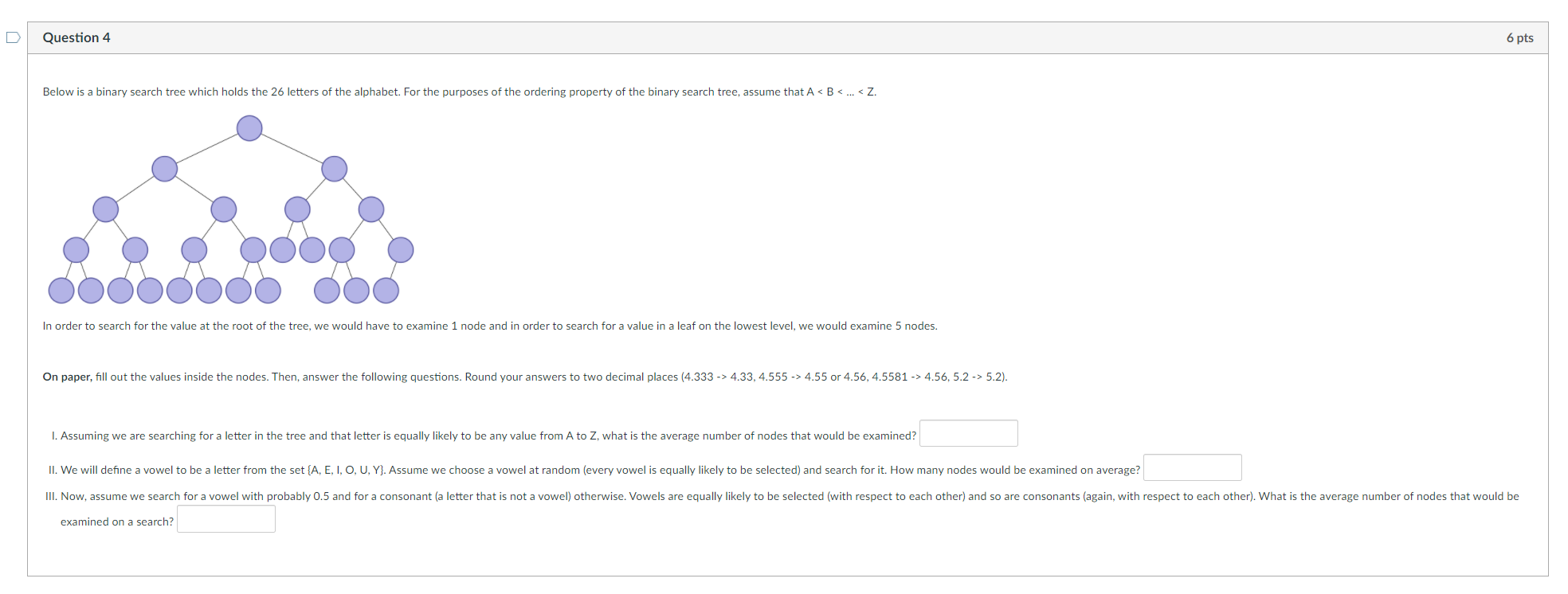
Question 4 6 pts Below is a binary search tree which holds the 26 letters of the alphabet. For the purposes of the ordering property of the binary search tree, assume that A 4.33, 4.555 -> 4.55 or 4.56, 4.5581 -> 4.56,5.2 -> 5.2). I. Assuming we are searching for a letter in the tree and that letter is equally likely to be any value from A to Z, what is the average number of nodes that would be examined? II. We will define a vowel to be a letter from the set (A, E, I, O, U, Y}. Assume we choose a vowel at random (every vowel is equally likely to be selected) and search for it. How many nodes would be examined on average? III. Now, assume we search for a vowel with probably 0.5 and for a consonant (a letter that is not a vowel) otherwise. Vowels are equally likely to be selected (with respect to each other) and so are consonants (again, with respect to each other). What is the average number of nodes that would be examined on a search