question 4 includes pseudocode from quicksort

question 4 is the 3rd picture and I needed all of them answered

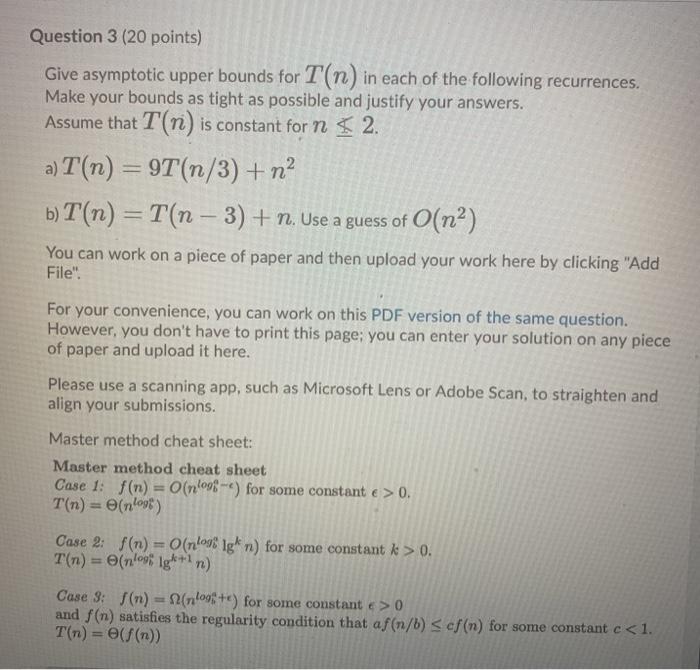
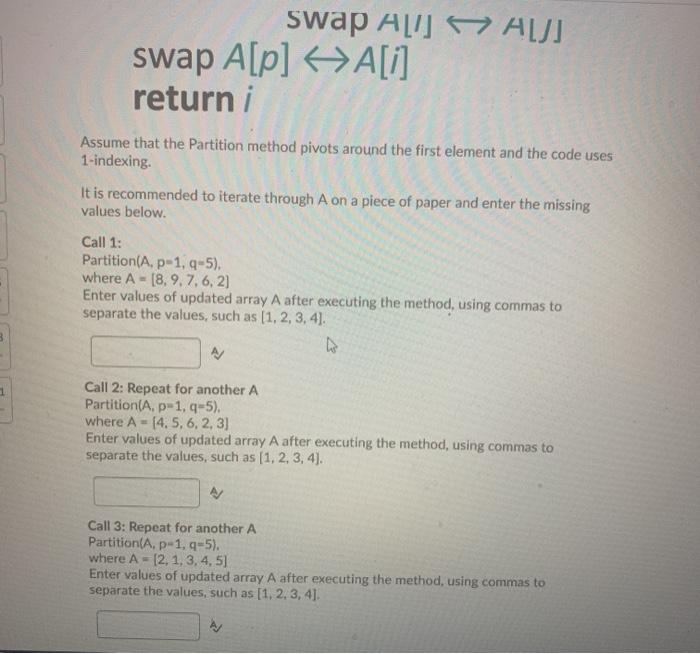
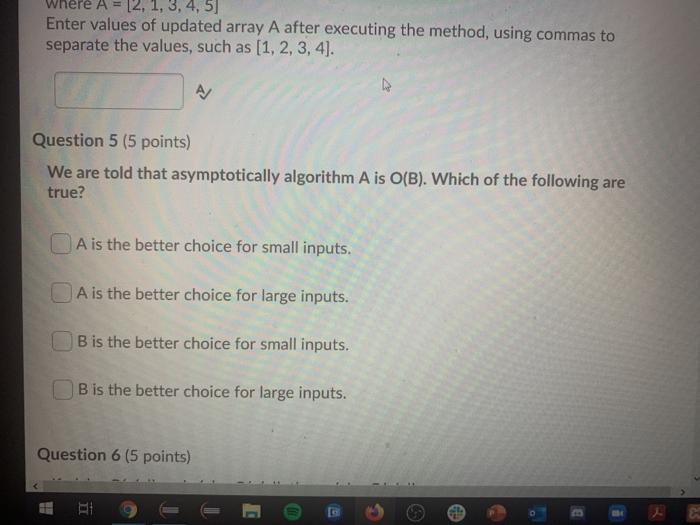
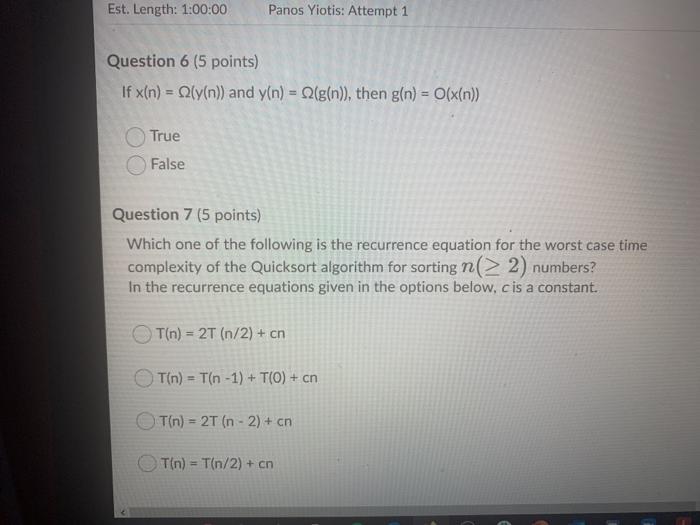
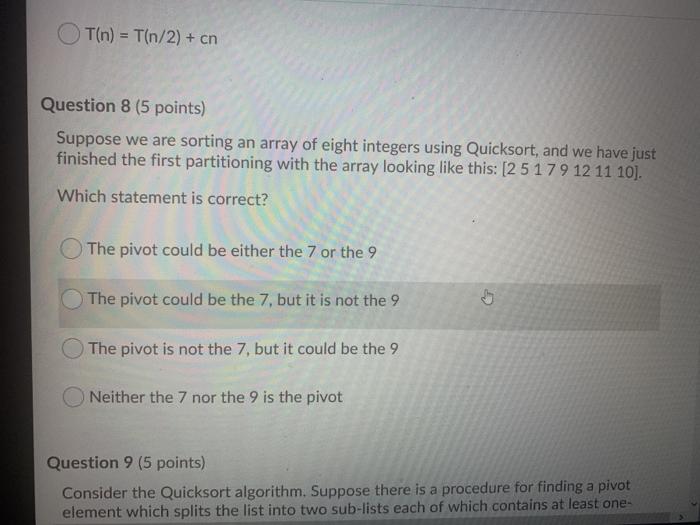
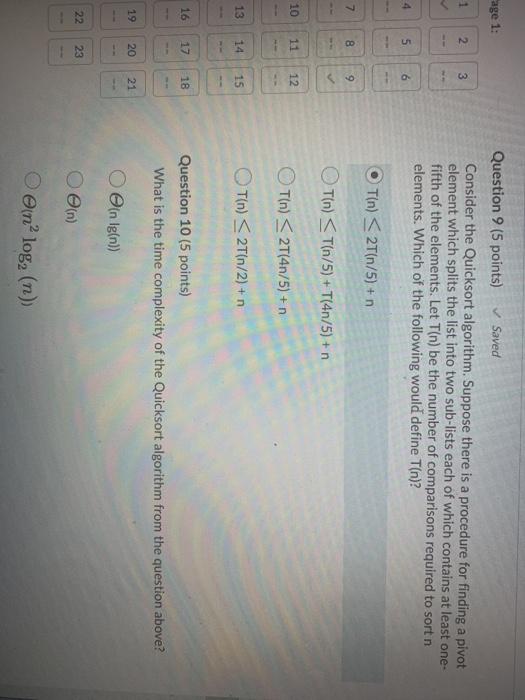
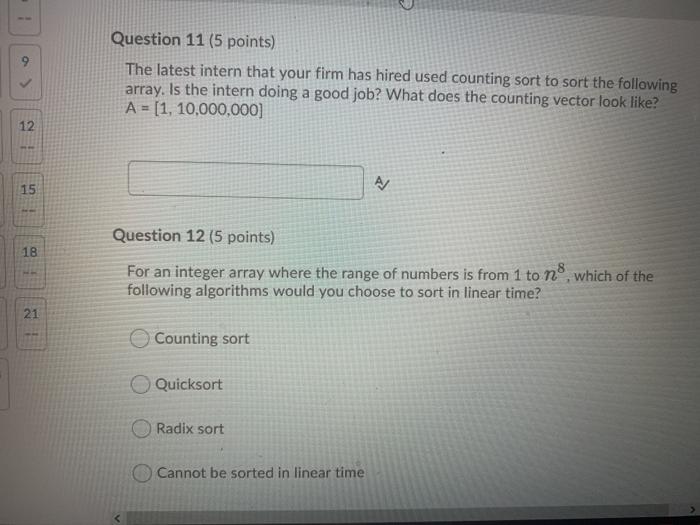
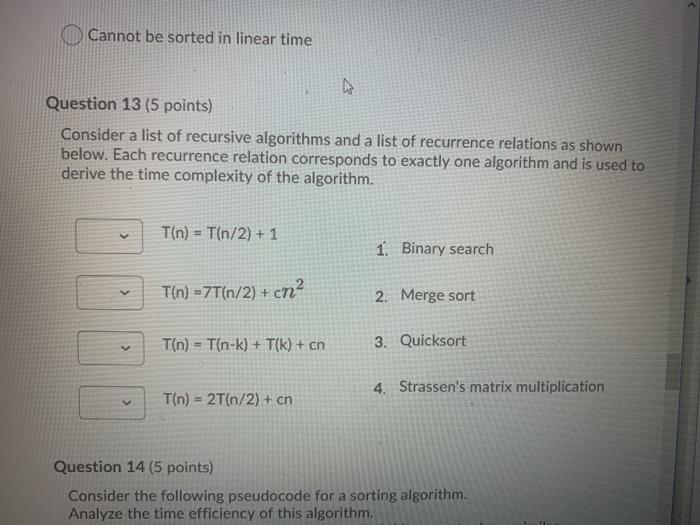
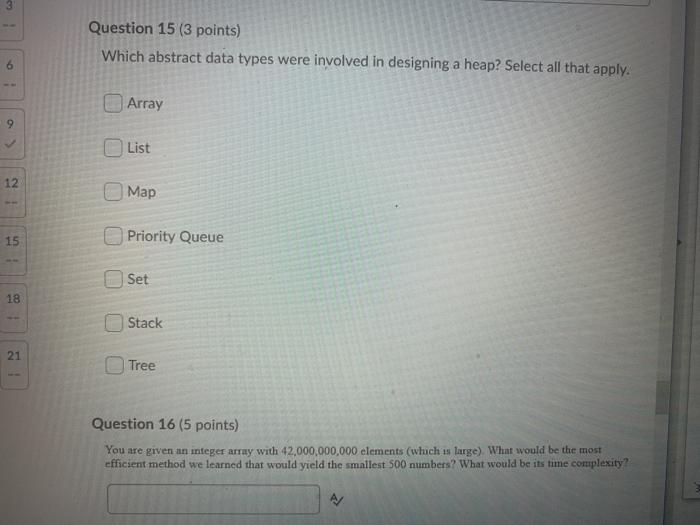
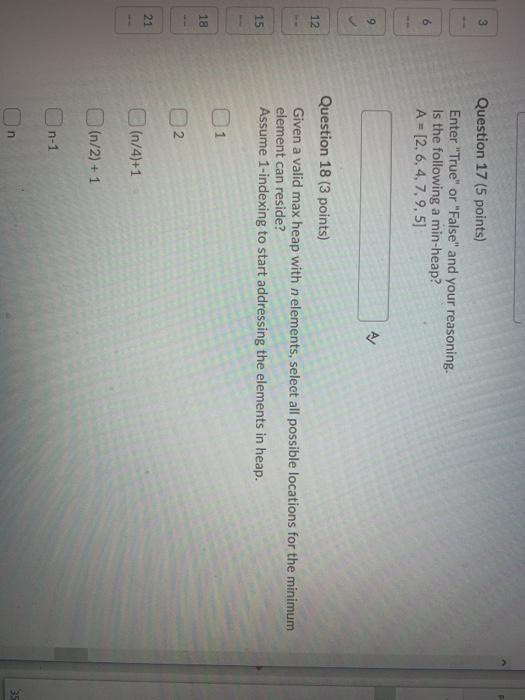
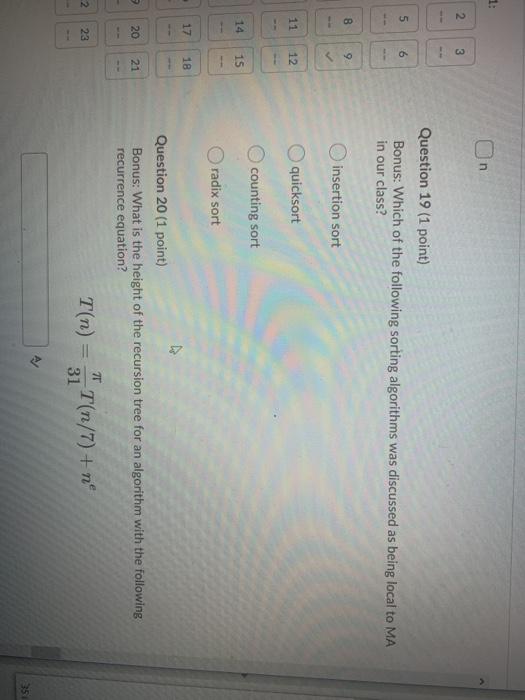
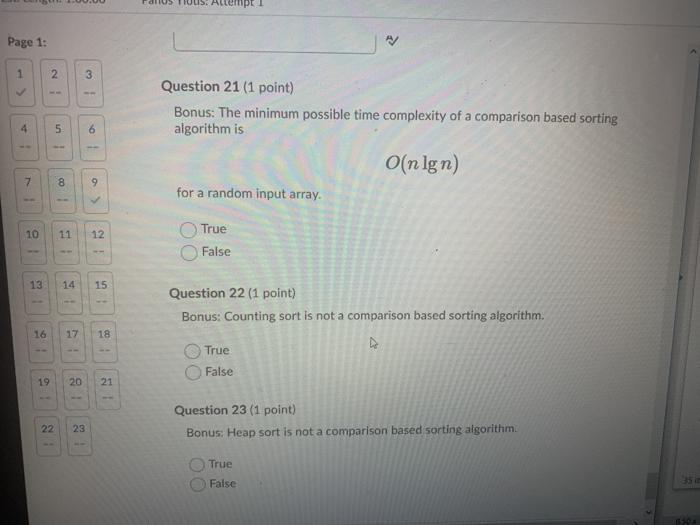
Question 2 (10 points) Rank the following functions by order of growth; that is, find an arrangement 91, 92, ..., 96 of the functions satisfying 91 12(92), 92 = N(93),...,95 = N2(96). Partition your list into equivalence classes such that functions f(n) and g(n) are in the same class if and only if f(n) = (g(n)). 00 (3/10)'n? {=0 321 3n > en > log: (n) > Question 3 (20 points) Give asymptotic upper bounds for T(n) in each of the following recurrences. Make your bounds as tight as possible and justify your answers. Assume that T(n) is constant for n 2. a) T(n) = 9T(n/3) + n2 b) T(n) = T(n 3) + n. Use a guess of O(na) You can work on a piece of paper and then upload your work here by clicking "Add File". For your convenience, you can work on this PDF version of the same question. However, you don't have to print this page; you can enter your solution on any piece of paper and upload it here. Please use a scanning app, such as Microsoft Lens or Adobe Scan, to straighten and align your submissions. Master method cheat sheet: Master method cheat sheet Case 1: f(n) = O(nlogg-e) for some constant e > 0. T(n) = now). Case 2: f(n) = O(nlogs ign) for some constant k > 0. T(n) = enle9 IgA+ n) Case 3: (n) = N(1098+) for some constant e > 0 and f(n) satisfies the regularity condition that af(n/b)