Question 4) Now, let's solve some optimisation problems. (a) Linearise the function at the point (3, 1). f(x, y) = ? 2x +

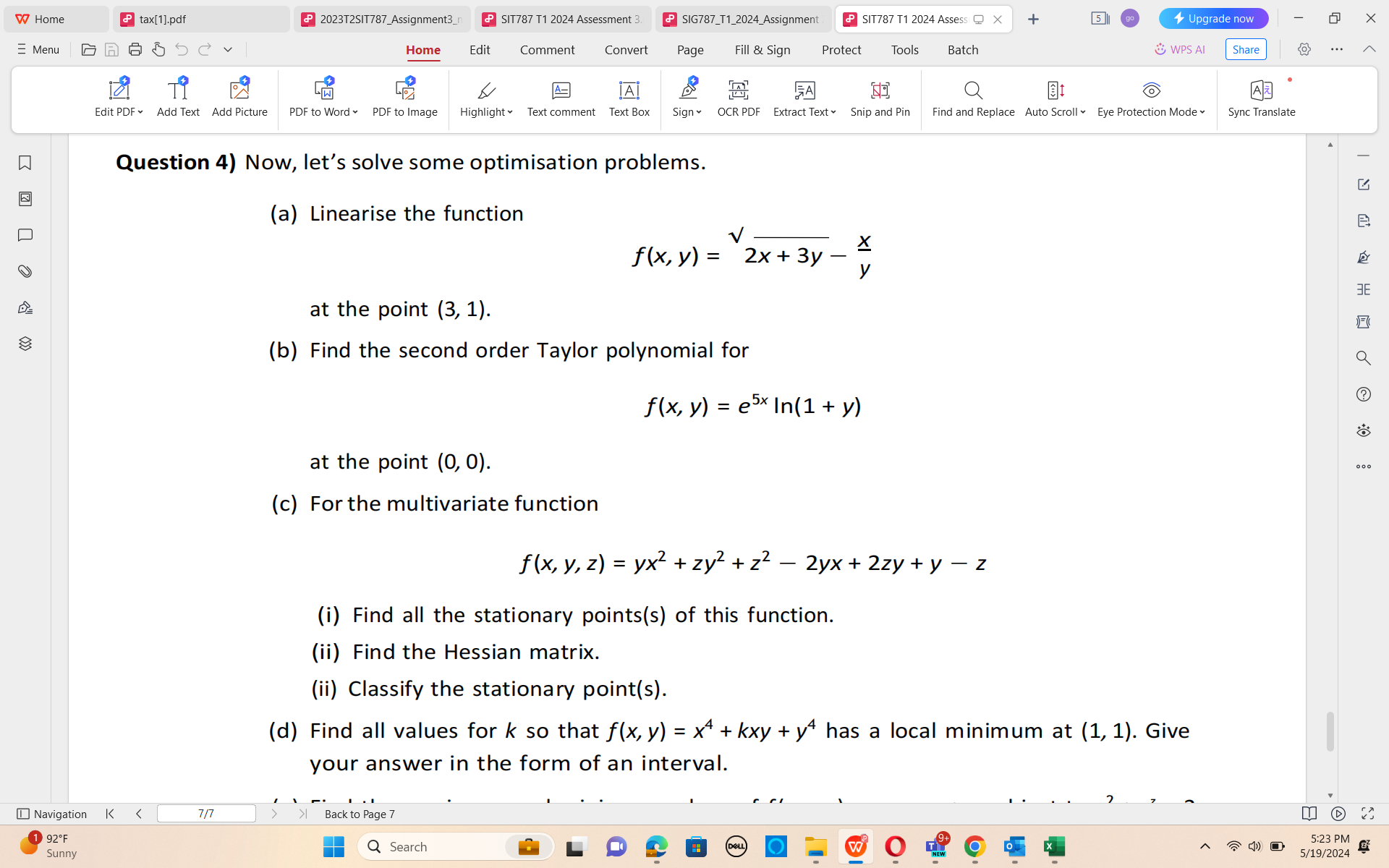
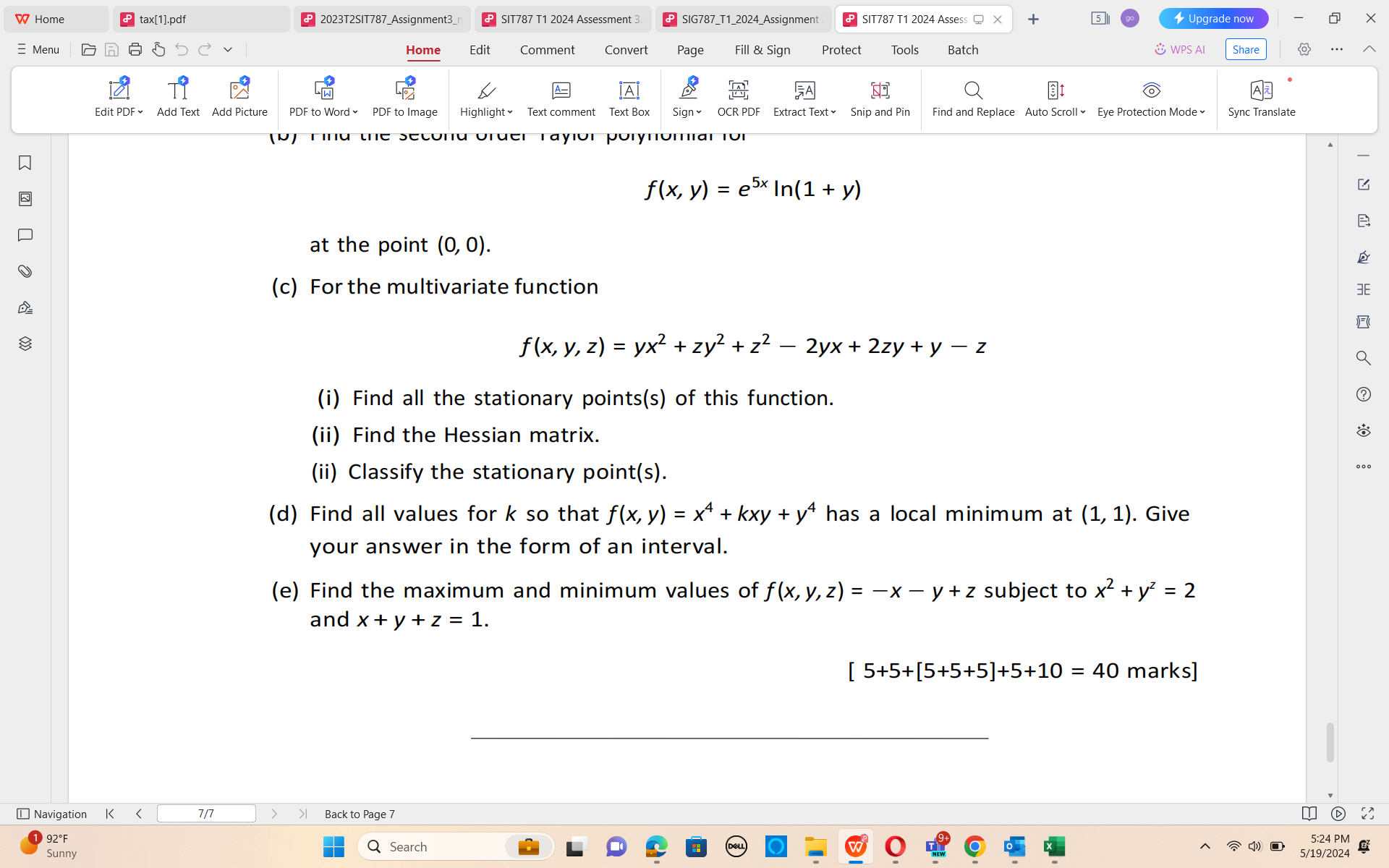
W Home tax[1].pdf P 2023T2SIT787_Assignment3_n P SIT787 T1 2024 Assessment 3. P SIG787_T1_2024_Assignment P SIT787 T1 2024 Assess @ X + Upgrade now X =Menu Home Edit Comment Convert Page Fill & Sign Protect Tools Batch & WPS AI Share ... TO A- IAI FA Q O Edit PDF . Add Text Add Picture PDF to Word . PDF to Image Highlight Text comment Text Box Sign OCR PDF Extract Text Snip and Pin Find and Replace Auto Scroll Eye Protection Mode Sync Translate W Question 4) Now, let's solve some optimisation problems. (a) Linearise the function f (x, y) = 2x+ 3y X IX PY 3E at the point (3, 1). (b) Find the second order Taylor polynomial for f (x, y) = esx In(1 + y) ? at the point (0, 0). (c) For the multivariate function f ( x, y, z) = yx2 + zy2 + z2 - 2yx + 2zy+ y- z (i) Find all the stationary points(s) of this function. (ii) Find the Hessian matrix. (ii) Classify the stationary point(s). (d) Find all values for k so that f(x, y) = x4 + kxy + y* has a local minimum at (1, 1). Give your answer in the form of an interval. Navigation K