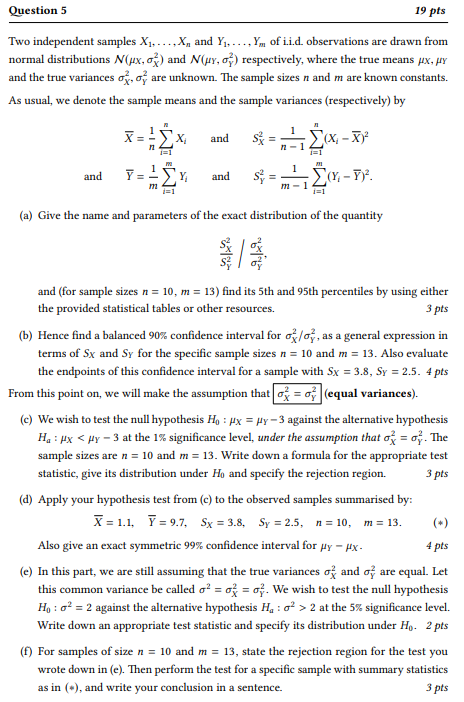
Question 5 19 pts Two independent samples X1, .... X, and Y1, .... Ym of iid. observations are drawn from normal distributions M(px, 3x) and N(ur, of) respectively, where the true means Ax, fy and the true variances ox, of are unknown. The sample sizes n and m are known constants. As usual, we denote the sample means and the sample variances (respectively) by = and SY = (X - XP and YELS YI and m - 1= 1 (a) Give the name and parameters of the exact distribution of the quantity and (for sample sizes n = 10, m = 13) find its 5th and 95th percentiles by using either the provided statistical tables or other resources. 3 pts (b) Hence find a balanced 90% confidence interval for ox/ov, as a general expression in terms of 5x and Sy for the specific sample sizes n = 10 and m = 13. Also evaluate the endpoints of this confidence interval for a sample with Sx = 3.8, Sy = 2.5. 4 pts From this point on, we will make the assumption that ox = oy (equal variances). (c) We wish to test the null hypothesis Ho : px = py -3 against the alternative hypothesis Ha:px 2 at the 5% significance level. Write down an appropriate test statistic and specify its distribution under Ho. 2 pts (f) For samples of size n = 10 and m = 13, state the rejection region for the test you wrote down in (e). Then perform the test for a specific sample with summary statistics as in (), and write your conclusion in a sentence. 3 pts