Question: Question 5 In this activity, you will work through a proof of a special case of Greeals The orem. In this special case: we only.r

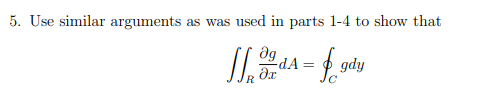
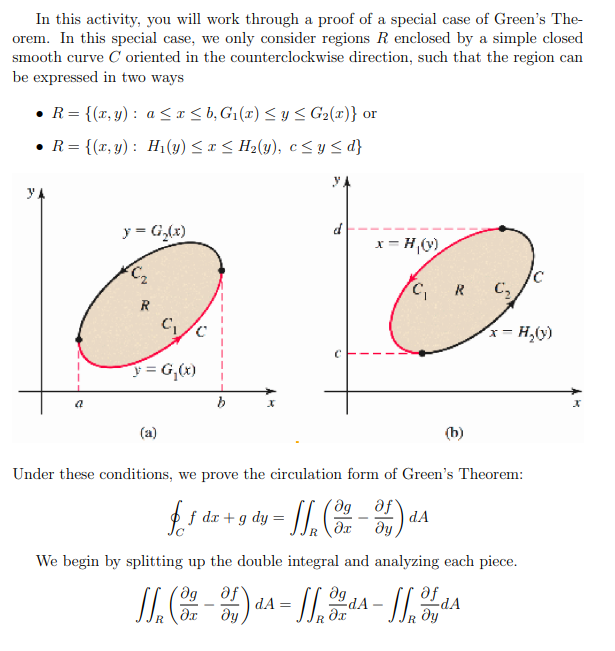
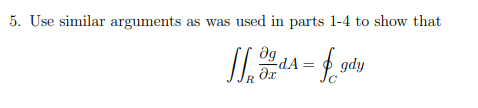
Question 5 In this activity, you will work through a proof

Question 5

we only.r consider regions R enclosed by a simple closed smooth curve

In this activity, you will work through a proof of a special case of Greeals The orem. In this special case: we only.r consider regions R enclosed by a simple closed smooth curve C oriented in the counterclockwise direction, such that the region can be expressed in two ways " R: {[319}: '3 E E E b1lii} i: y E 92(3)} 01' I R={[2'.,y]|= H1{y}EIEH2{yLCEyE-i} Under these conditions, we prove the circulation form of Green's Theorem: Mm -fl(3:-3-Dd We begin by splitting up the double integral and analyzing each piece. mesQM 11% we 1. Show that I, ada = [ (s(z. G2( z) - f(x, G.(z) de 2. Notice that, over the interval a

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Question 2 In this activity, you will work through a proof of a special case of Green's The- orem. In this special case, we onlj},r consider regions R enclosed by a simple closed smooth curve C...

Question 3 In this activity, you will work through a proof of a special case of Green's The- orem. In this special case, we only consider regions R enclosed by a simple closed smooth curve C oriented...

Question 4 In this activity, you will work through a proof of a special case of Green's The- orem. In this special case, we only consider regions R enclosed by a simple closed smooth curve C oriented...

In this activity, you will work through a proof of a special case of Green's The- orem. In this special case, we only consider regions R enclosed by a simple closed smooth curve C oriented in the...

GSH TERM-CONTRACTING IRREGULARITIES Background The Government Services Handling (GSH), frequently referred to as the housekeeper of the Federal Government," is an agency that deals in a vast range...

Walter Construction Group Lid v CPL (Surry Hills) Ply Lid [2003] Adj-L.R. 04/09 JUDGMENT : Nicholas J : Supreme Court of New South Wales : 9" April 2003. 1 By Its Notice of Motion the Plaintiff seeks...

1 GSH TERM-CONTRACTING IRREGULARITIES Background The Government Services Handling (GSH), frequently referred to as the housekeeper of the Federal Government," is an agency that deals in a vast range...

Background The Government Services Handling (GSH), frequently referred to as the housekeeper of the Federal Government," is an agency that deals in a vast range and variety of contracting and...

GSH TERM-CONTRACTING IRREGULARITIES Background The Government Services Handling (GSH), frequently referred to as the housekeeper of the Federal Government," is an agency that deals in a vast range...

Based on given project, without using packet tracer, what is the 4 main steps to configure VLANs for network as shown below. Give the configuration in one line with description of each steps PC-P...

The yearly tuition costs in dollars for random samples of medical schools that specialize in research and in primary care are listed. At = 0.05, can it be concluded that a difference between the...

The Fisher effect primarily emphasizes the impact of on an investor's rate of return. 2 5 Multiple Choice inflation the time to maturity default

1. Introduction 2. What were business objectives of the campaign? 3. Conculsion few sentences each questions Caf de Colombia In mid-December 2000, Dr. Jorge Crdenas Gutirrez, general manager of the...

9. What type of competence is important to have and develop in order to strengthen the core value you want others to associate with you?

6. Identify a core value that is important to you and that you would like to strengthen in yourself. Write down this core value. Then complete the follow-ing sentence: This core value is important to...

13. In the statements below, put a cross for the statement you feel characterizes yourself best when you communicate with others. Its not necessarily the way you know you should communicate, but the...