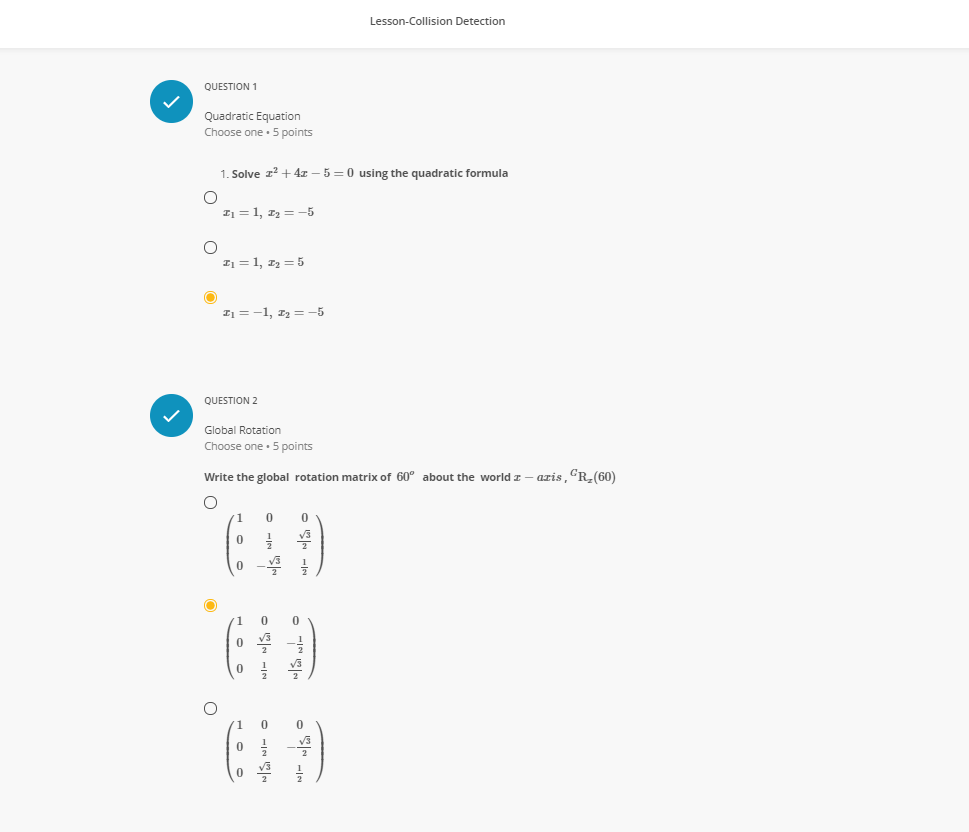
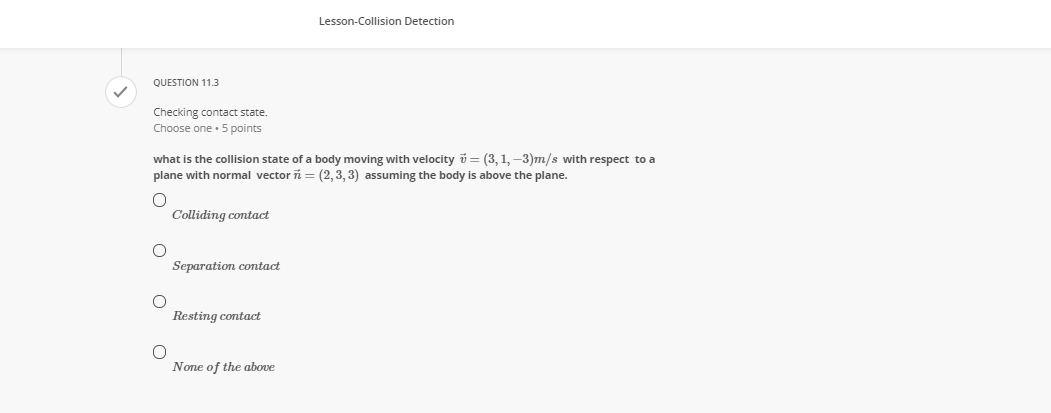
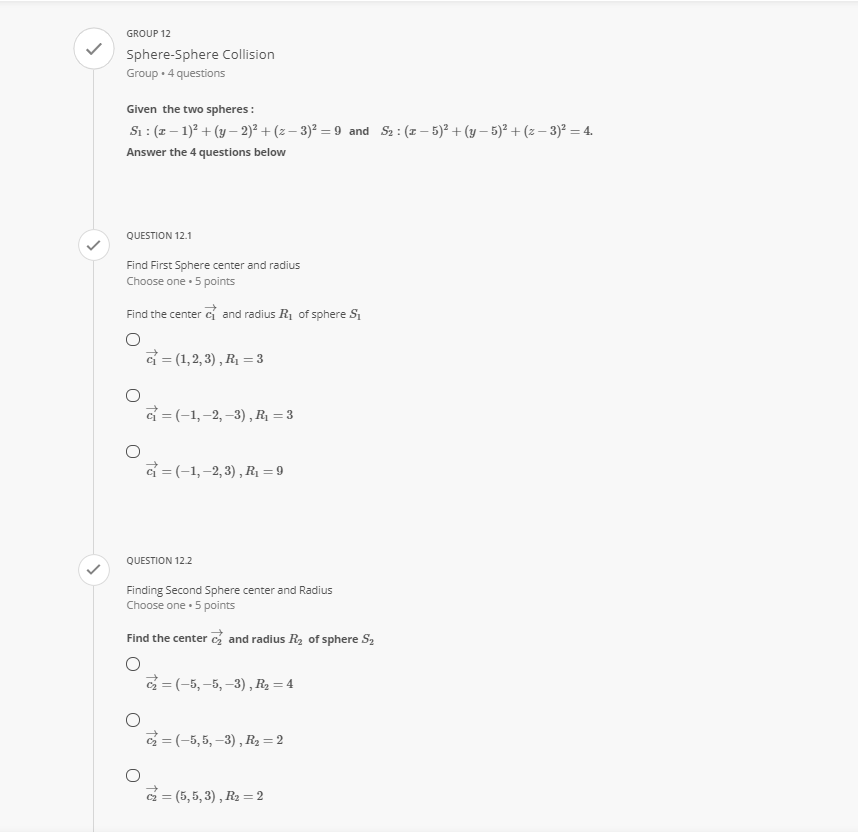
Question: QUESTION 8 V Transforming a Point from Local Space to World Space Choose one . 5 points A box is located at & = (2,
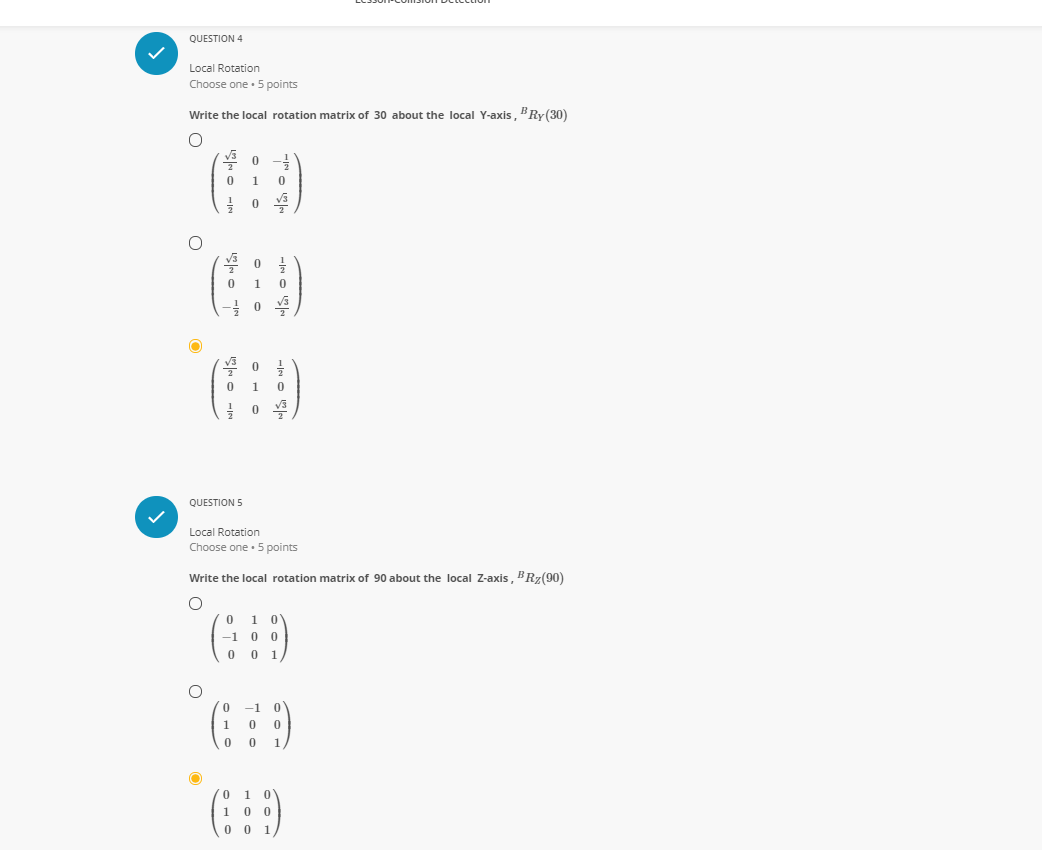
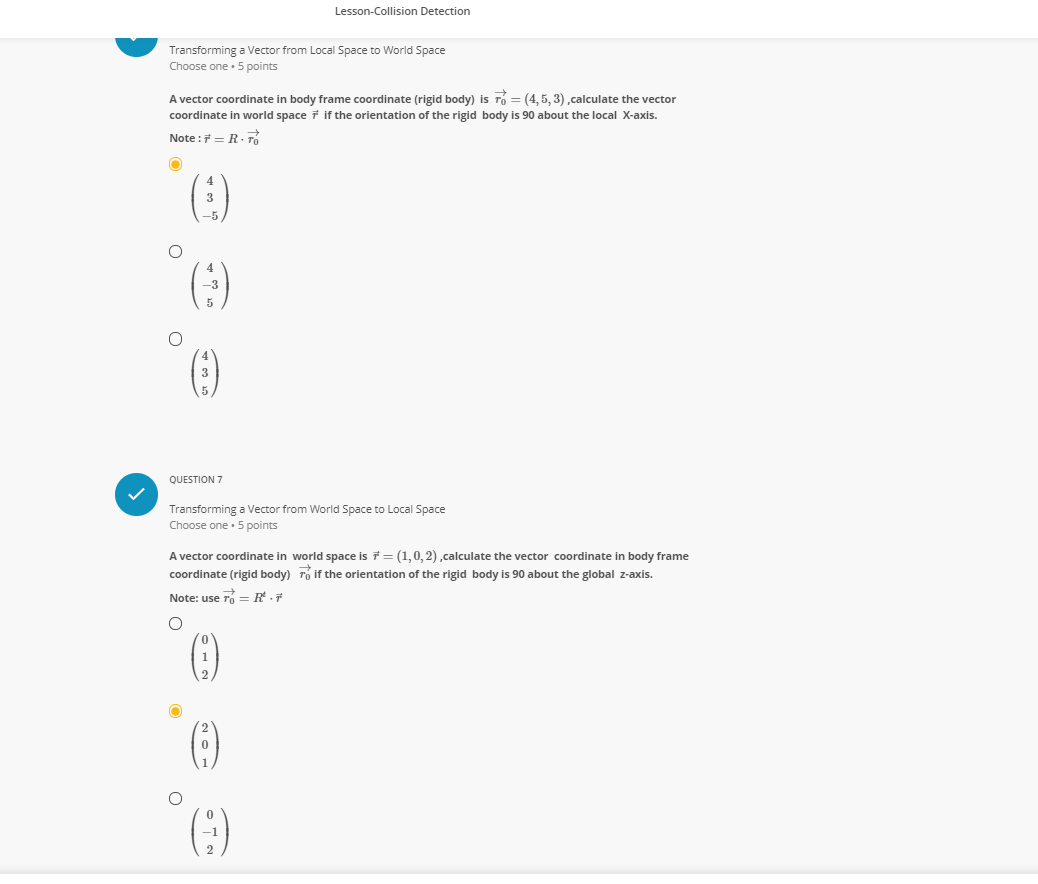
QUESTION 8 V Transforming a Point from Local Space to World Space Choose one . 5 points A box is located at & = (2, 1, 0) with orientation of 90 degree about the global x-axis. Calculate the position Pworld of a point in world space if the point coordinate in local space is Plocal =(4,0,2). Note : use Pworld = C + R . To O 6 O QUESTION 9Lesson-Collision Detection QUESTION 1 Quadratic Equation Choose one . 5 points 1. Solve T' + 4x -5 =0 using the quadratic formula O I1 = 1, 12 = -5 O $1 = 1, 12 = 5 O $1 =-1, 12 = -5 QUESTION 2 Global Rotation Choose one . 5 points Write the global rotation matrix of 60" about the world r - aris, "R.(60) O 0 O OQUESTION 3 V Global Rotation Choose one . 5 points Write the global rotation matrix of 45" about the world y-axis, "Ry(45) O O OQUESTION 4 Local Rotation Choose one . 5 points Write the local rotation matrix of 30 about the local Y-axis , #Ry (30) O 0 O QUESTION 5 Local Rotation Choose one . 5 points Write the local rotation matrix of 90 about the local Z-axis , #Ry(90) O 0 1 -10 0 O -1 O 1 0Lesson-Collision Detection Transforming a Vector from Local Space to World Space Choose one . 5 points A vector coordinate in body frame coordinate (rigid body) is ro = (4, 5, 3) , calculate the vector coordinate in world space 7 if the orientation of the rigid body is 90 about the local X-axis. Note : F = R . To O O CT CO QUESTION 7 Transforming a Vector from World Space to Local Space Choose one . 5 points A vector coordinate in world space is 7 = (1, 0,2), calculate the vector coordinate in body frame coordinate (rigid body) To if the orientation of the rigid body is 90 about the global z-axis. Note: use To = R . F C HON O N LeQUESTION 8 V Transforming a Point from Local Space to World Space Choose one . 5 points A box is located at & = (2, 1,0) with orientation of 90 degree about the global x-axis. Calculate the position Pworld of a point in world space if the point coordinate in local space is Plocal=(4,0,2). Note : use Pworld = C + R . To O 6 O O NORLesson-Collision Detection GROUP 10 Sphere Equation Group . 4 questions A sphere is the set of points p = (I, y, 2)in 3D space that have a constant distance called the radius R with a fixed point d = (a, b, c) defined as the sphere center. The sphere algebraic equation is : (x - a) + (y - b)3 + (z - c)? = 12 where a, b, c are the components of the center QUESTION 10.1 Finding a Sphere Center and Radius Choose one . 5 points Find the center c and radiusr of the sphere S : (2 + 7)? + (y - 4) + (2 +9)2 =36 O 2 = (7, -4, 9), T = 6 O 2 = (-7, 4, -0 ), T = 6 2 = (7, -4, 9), T = 36 QUESTION 10.2 Finding a Sphere Center and Radius Choose one . 5 points Find the center d and radius r of the sphere S : (x + 1)3 + (y -2)3 + (2 -2)3 =4 O 2 = (-1, 2, 2 ), T = 2 * = (-1, 2, 2 ), r = 4 O c = (1, -2, - 2), r = 2QUESTION 10.3 Writing the Equation of a Sphere Given its Center and Radius Choose one . 5 points Write the equation of a sphere with center & = (2, 1, -5) and radius R = 3 O (1 - 2)3 + (y - 1)3 + (2+5)?=0 O (1 - 2)3 + (y - 1)3 + (2+ 5)? =3 O (z + 2)3 + (y + 1)2 + (2-5)3=9 QUESTION 10.4 V Writing the Equation of a Sphere Given its Center and Radius Choose one . 5 points Write the equation of a sphere with center c = (3, 2, 1) and radius R = 5 O (1 - 3)3 + (y - 2)2 + ( 2 - 1)2=25 O (1 - 3)2 + (y -2)3 + (2 - 1)? =5 O (z + 3)3 + (y + 2)3 + (2 + 1)2=5Lesson-Collision Detection GROUP 11 Colliding Contact, Separation Contact, and Resting Contact Group . 3 questions QUESTION 11.1 Checking contact state. Choose one . 5 points what is the collision state of a body moving with velocity u = (2, -3, 1)m/s with respect to a plane with normal vector ni = (0, 1, 0) assuming the body is above the plane. Colliding contact O Separation contact O Resting contact O None of the above QUESTION 11.2 Checking contact state. Choose one . 5 points what is the collision state of a body moving with velocity u = (1, 2, 4)m/s with respect to a plane with normal vector n = (1, 1, 0) assuming the body is above the plane. O Colliding contact O Separation contact O Resting contact O None of the aboveLesson-Collision Detection QUESTION 11.3 V Checking contact state. Choose one . 5 points what is the collision state of a body moving with velocity u = (3, 1, -3)m/s with respect to a plane with normal vector ni = (2, 3, 3) assuming the body is above the plane. O Colliding contact O Separation contact O Resting contact O None of the aboveGROUP 12 Sphere-Sphere Collision Group . 4 questions Given the two spheres : Si : (x - 1)3 + (y - 2)3 + (2 -3)3 -9 and $2 : (x - 5)' + (y - 5)3 + (2 -3)? = 4. Answer the 4 questions below QUESTION 12.1 Find First Sphere center and radius Choose one . 5 points Find the center cf and radius R, of sphere S, O Ci = (1, 2, 3 ) , R1 = 3 O Ci = (-1, -2, -3) , R1 = 3 O c = (-1, -2, 3 ) , R1 = 9 QUESTION 12.2 Finding Second Sphere center and Radius Choose one . 5 points Find the center cy and radius Ry of sphere $2 O C = (-5, -5, -3), R2 =4 O C = (-5, 5, -3) , R2 = 2 O 2 = (5,5,3) , R2 = 2Lesson-Collision Detection QUESTION 12.2 Finding Second Sphere center and Radius Choose one . 5 points Find the center co and radius Ry of sphere S2 O C = (-5, -5, -3) , R2 = 4 O C = (-5,5, -3) , R2 = 2 O C = (5, 5,3) , R2 = 2 QUESTION 12.3 Find the Distance between the two Spheres Choose one . 5 points Calculate the distance cici between the two sphere positions O CC = 25 O GC = 5 O ac =1 QUESTION 12.4QUESTION 12.3 Find the Distance between the two Spheres Choose one . 5 points Calculate the distance cici between the two sphere positions O CIC2 = 25 O 9G = 5 O CG = 1 QUESTION 12.4 Collision between two Sphers Choose one . 5 points Is there any collision between the 2 spheres ? O collision, ci Ri+ R2 O No collision, cici > Rit Re O None of the above