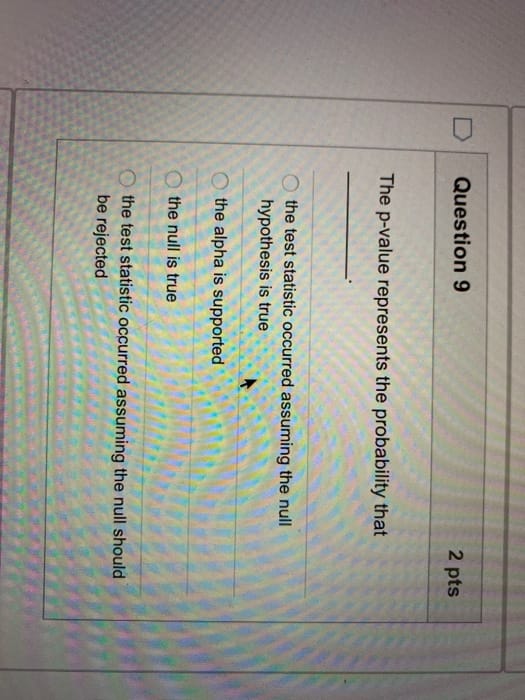
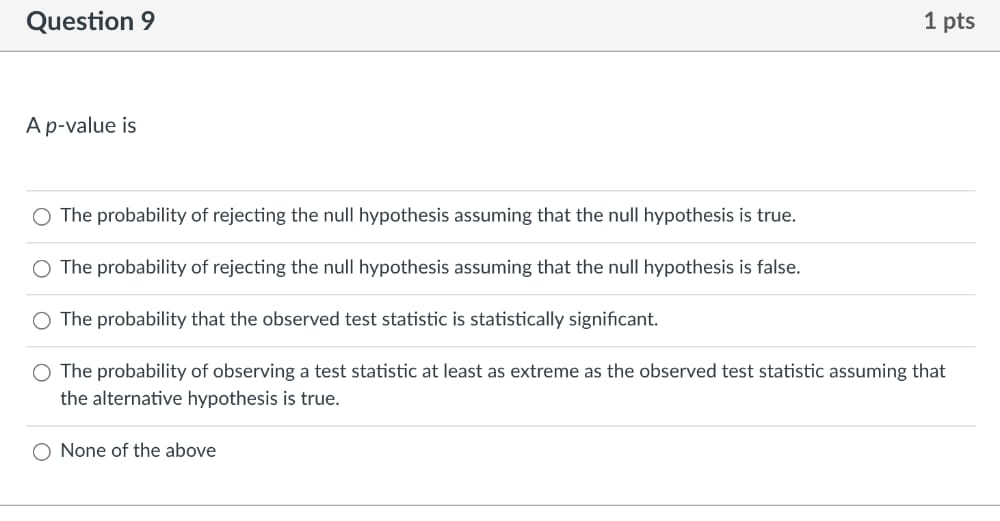
Question: Question 9 2 pts The p-value represents the probability that the test statistic occurred assuming the null hypothesis is true Othe alpha is supported O


Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


