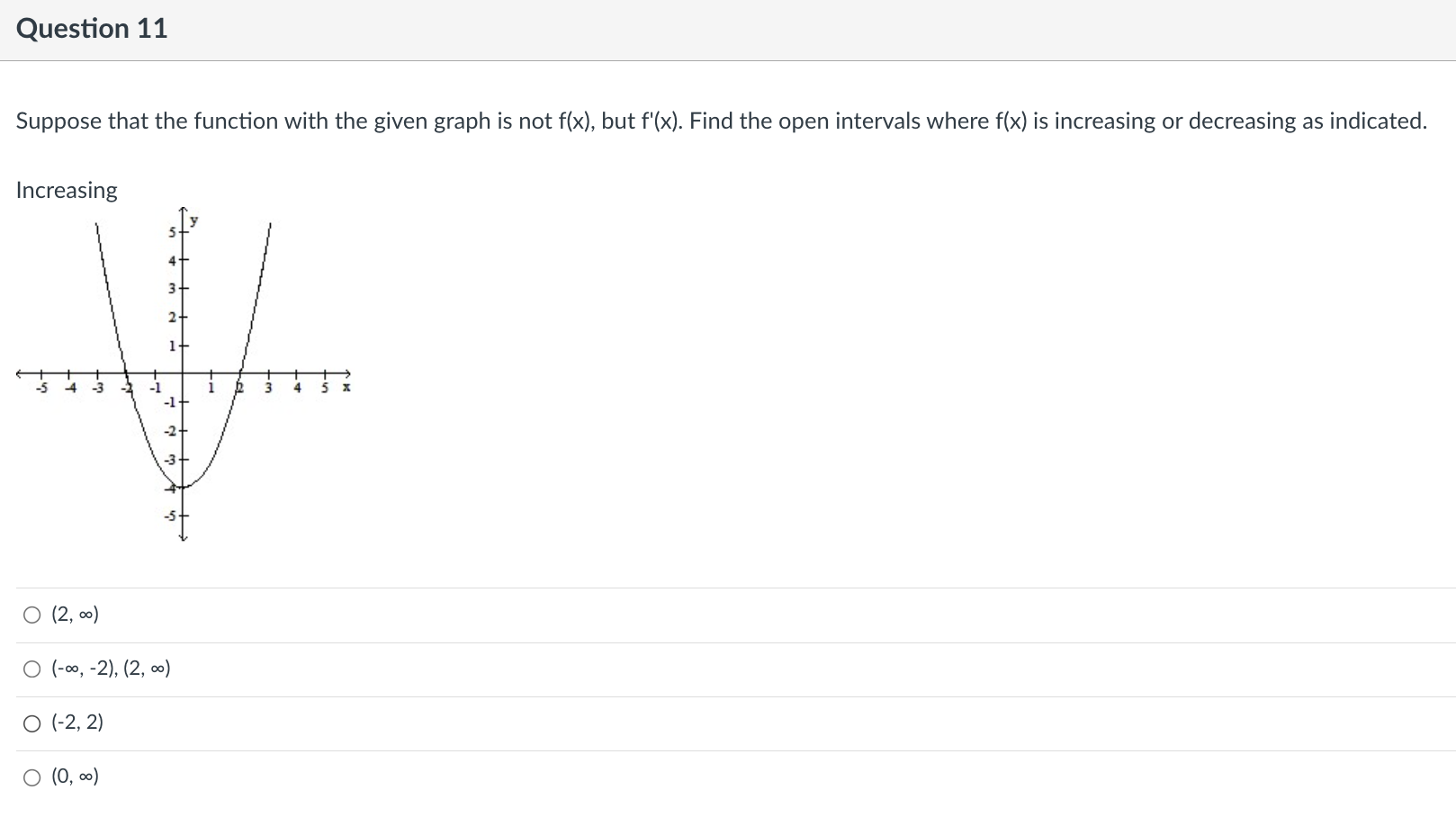
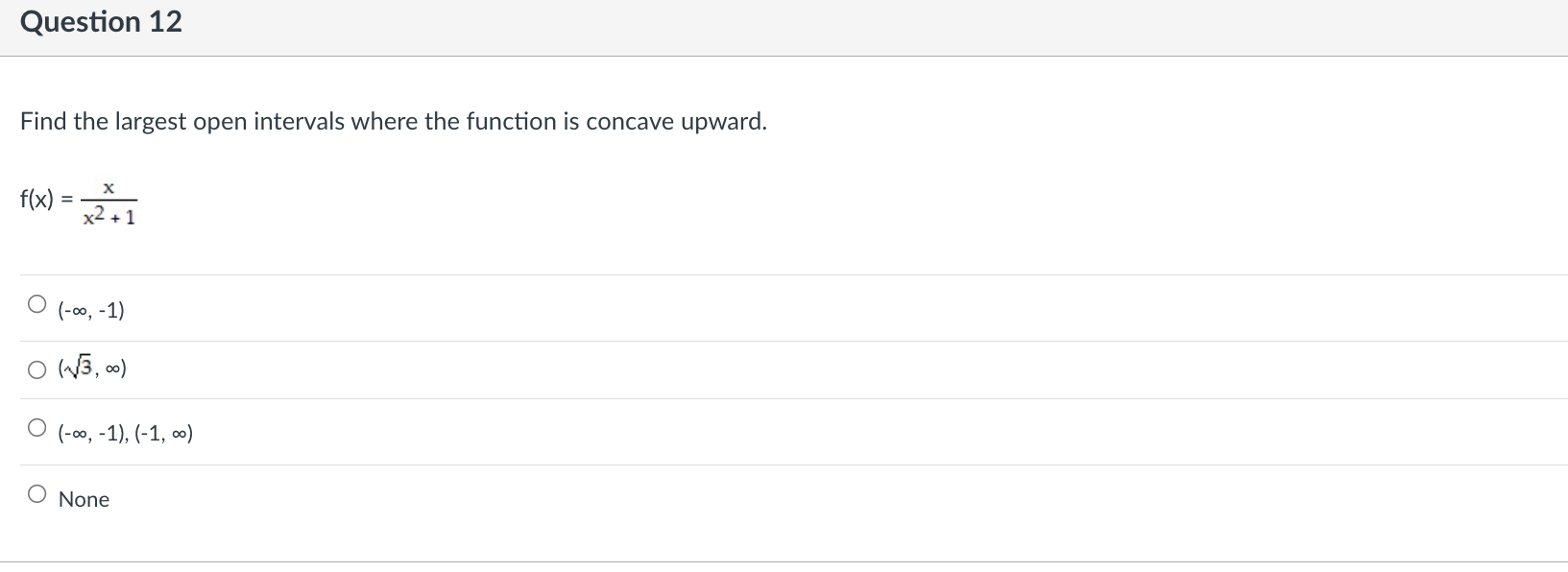
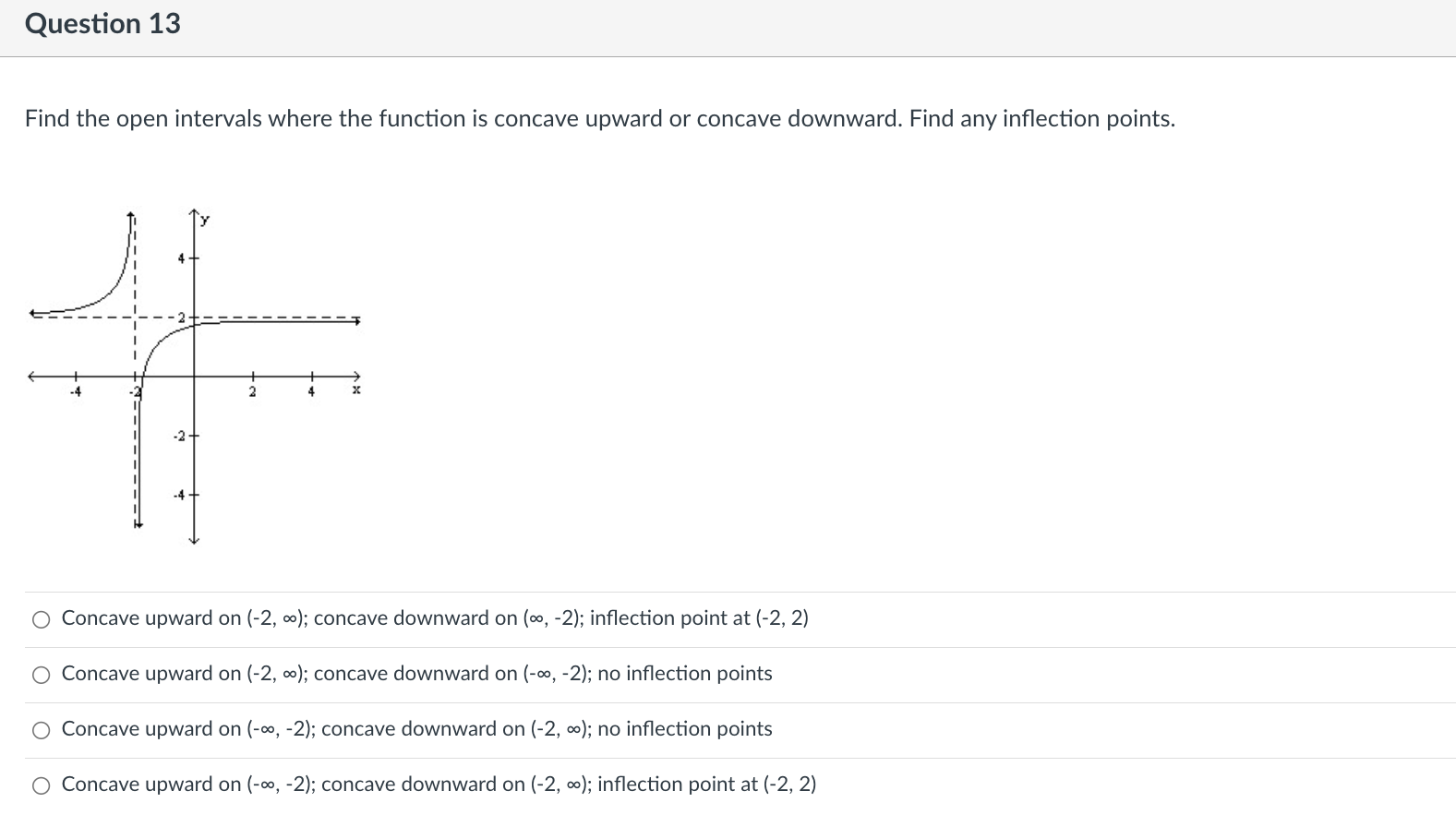
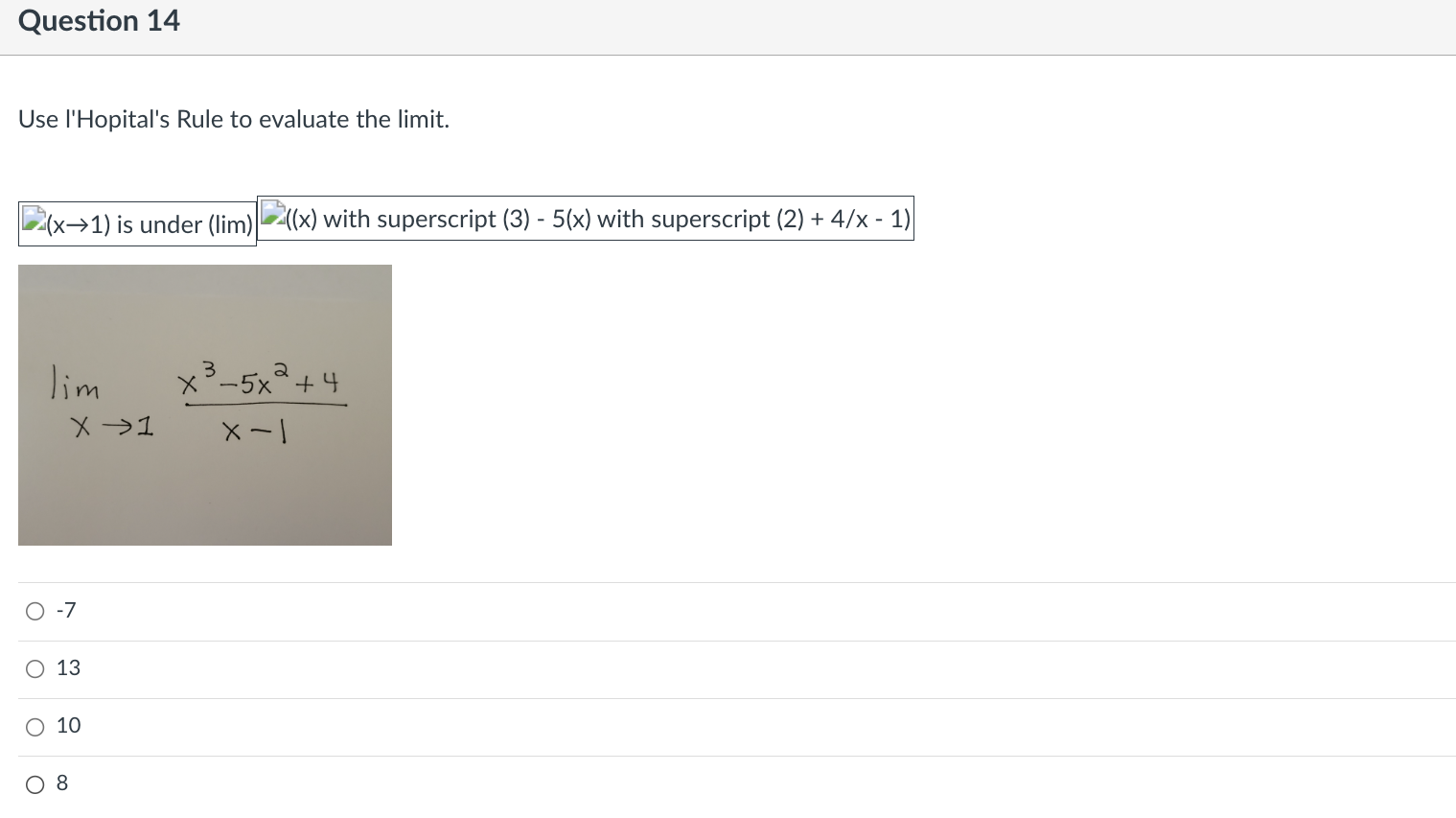
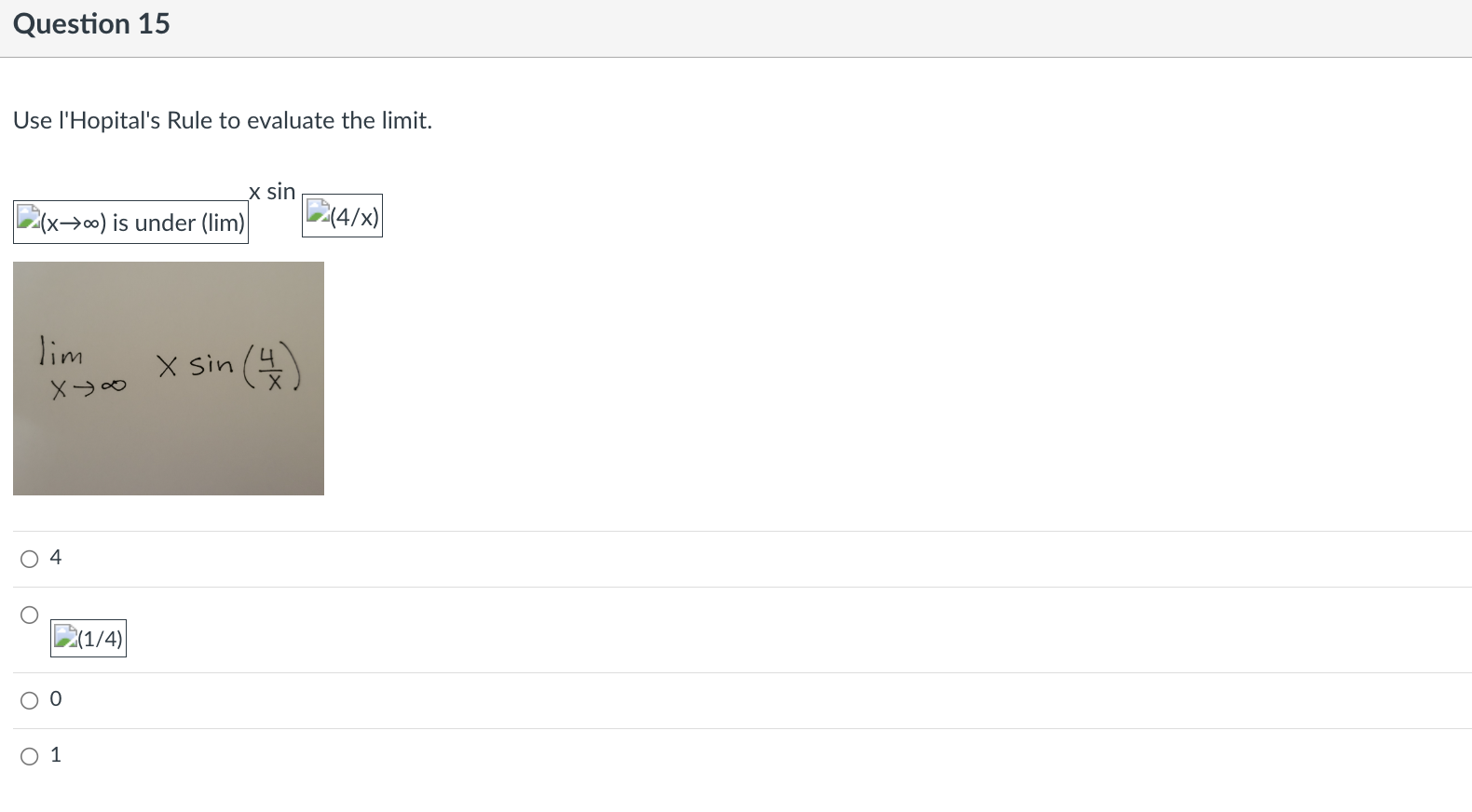
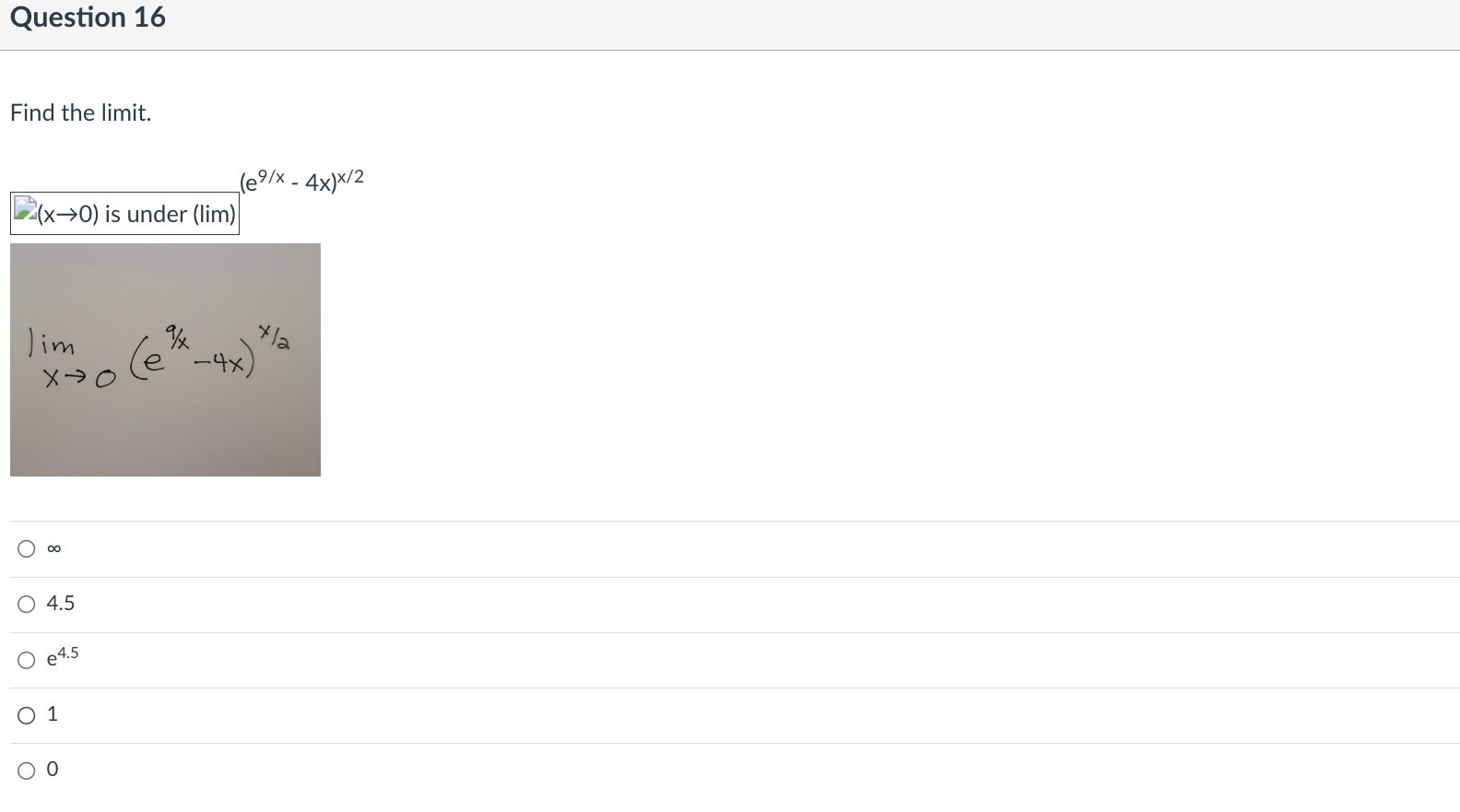
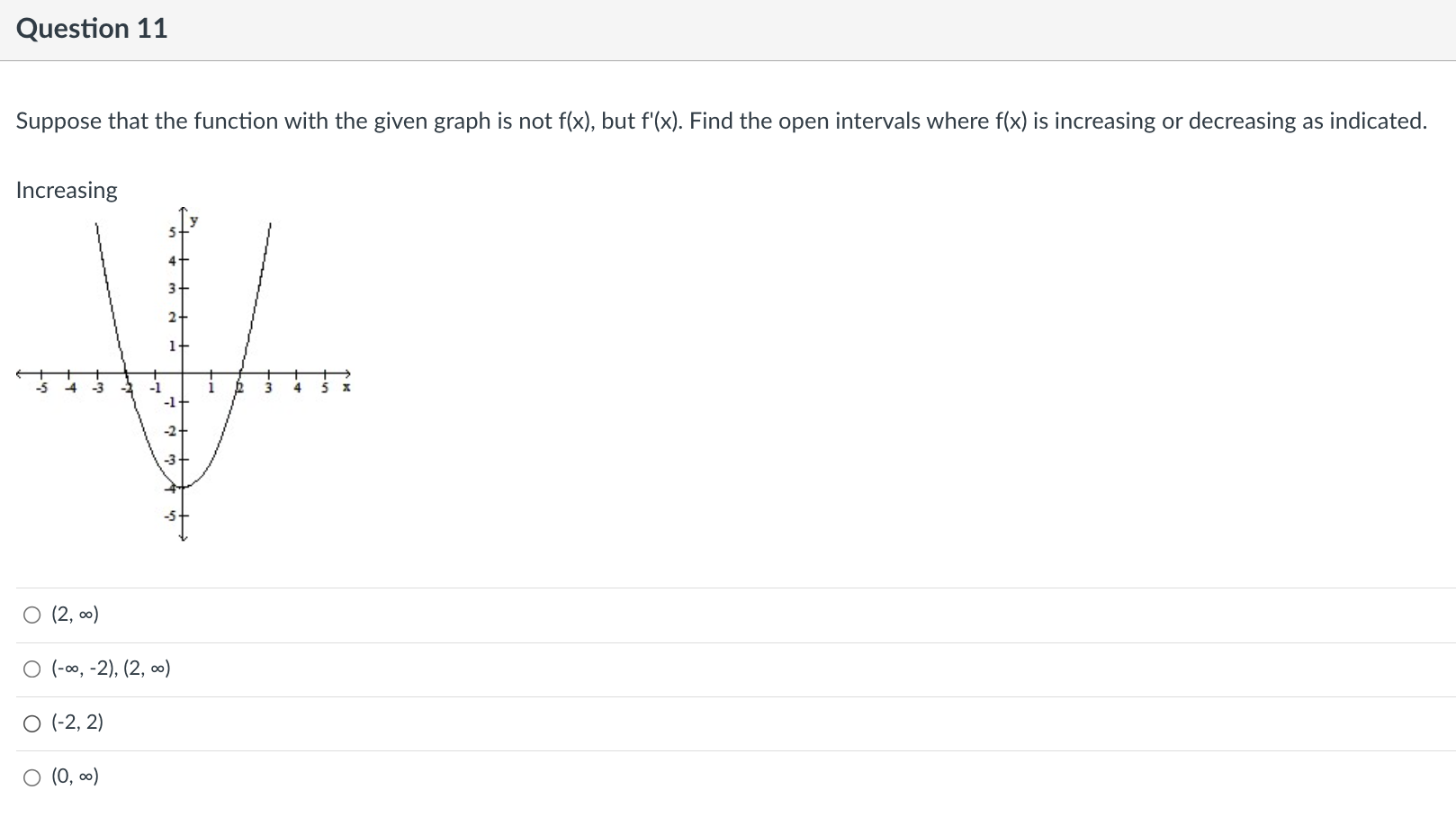
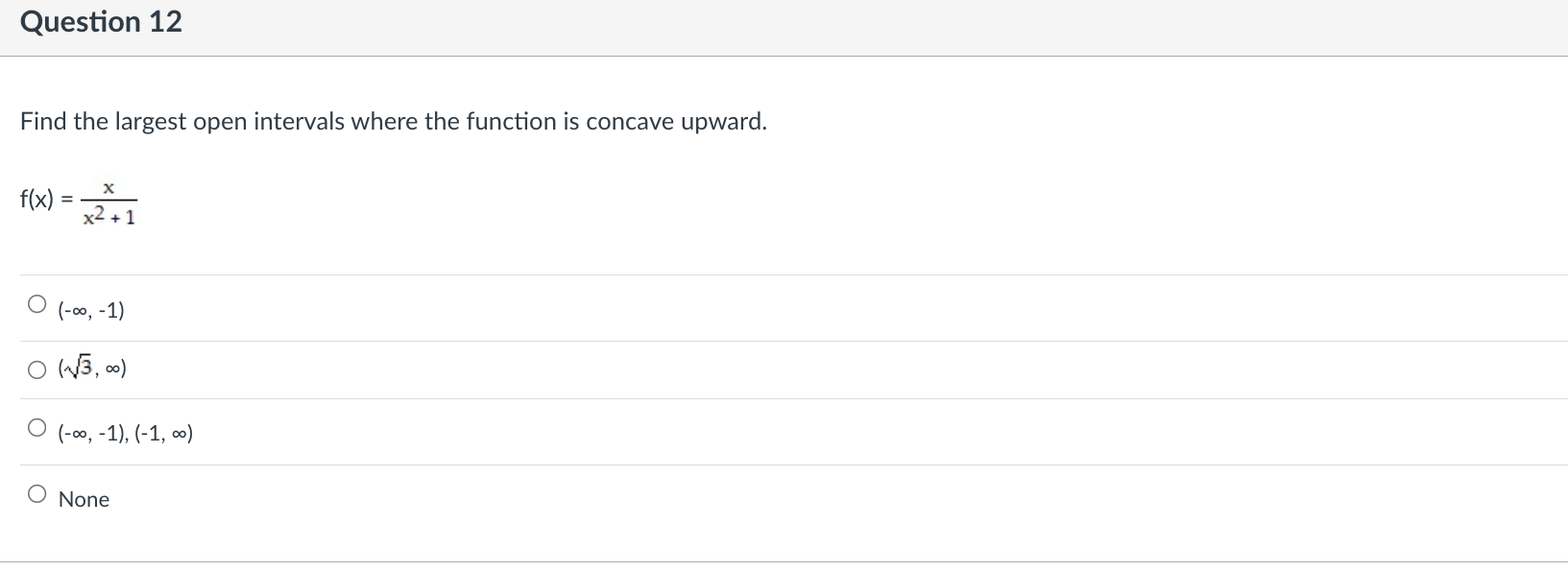
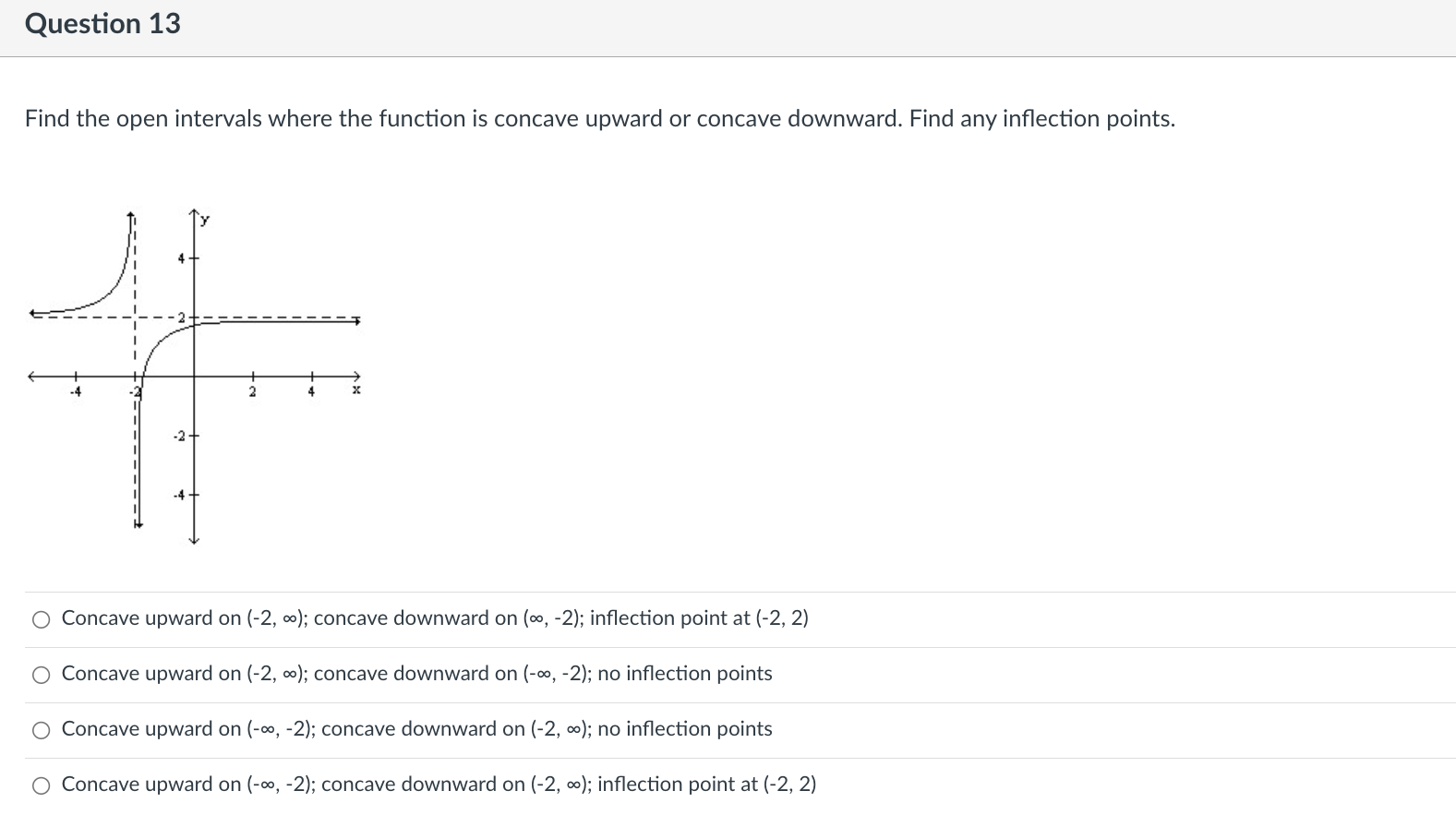
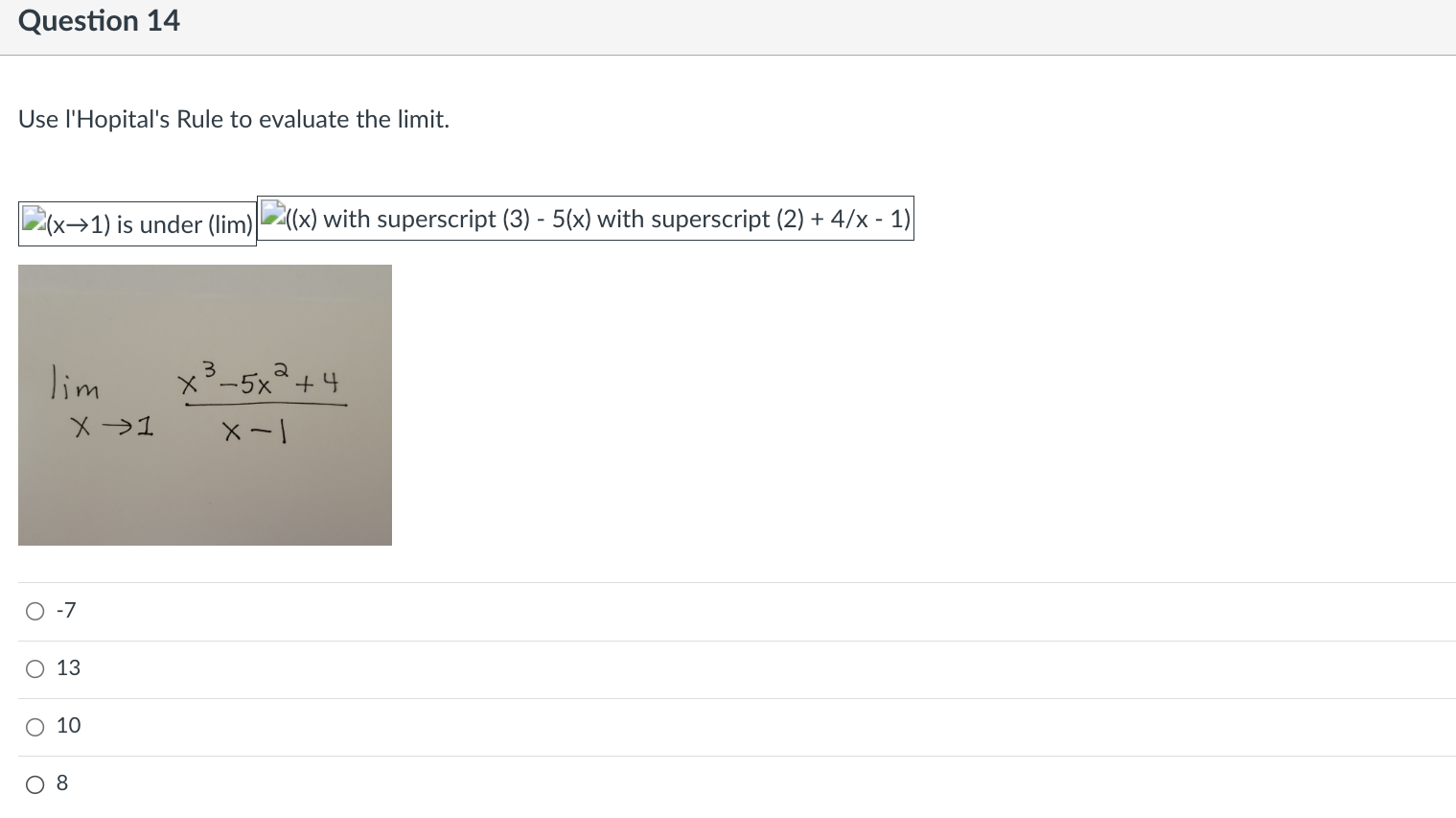
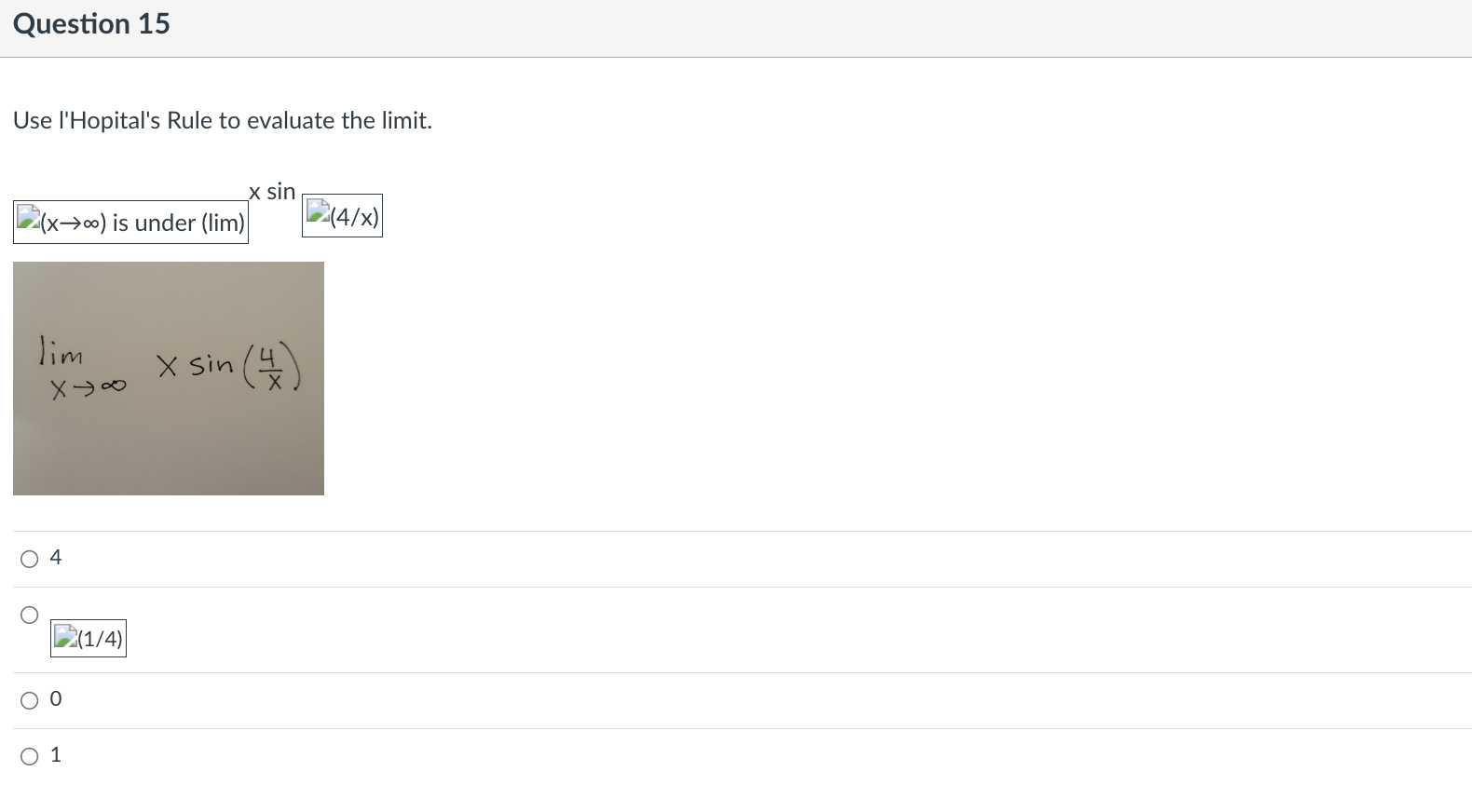
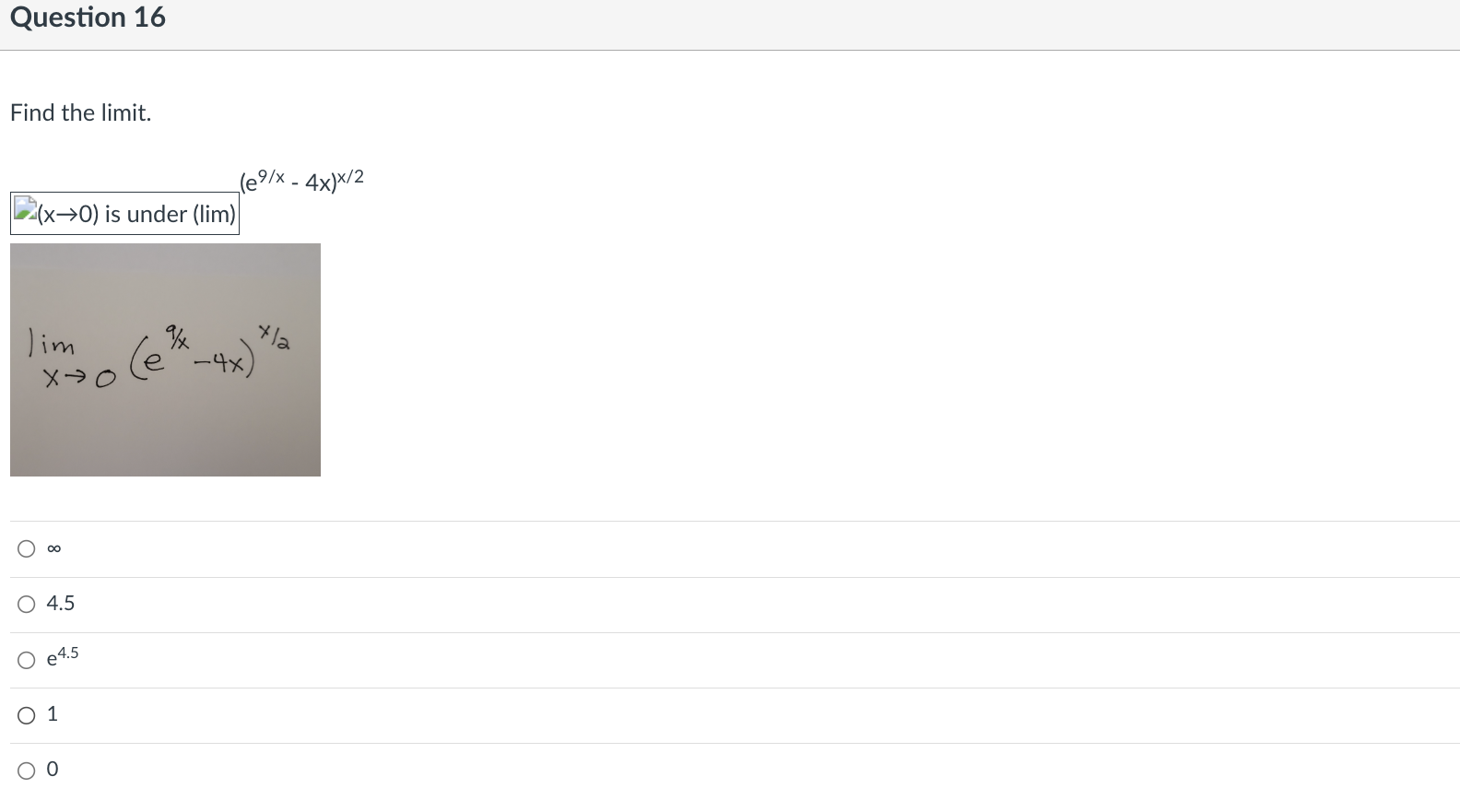
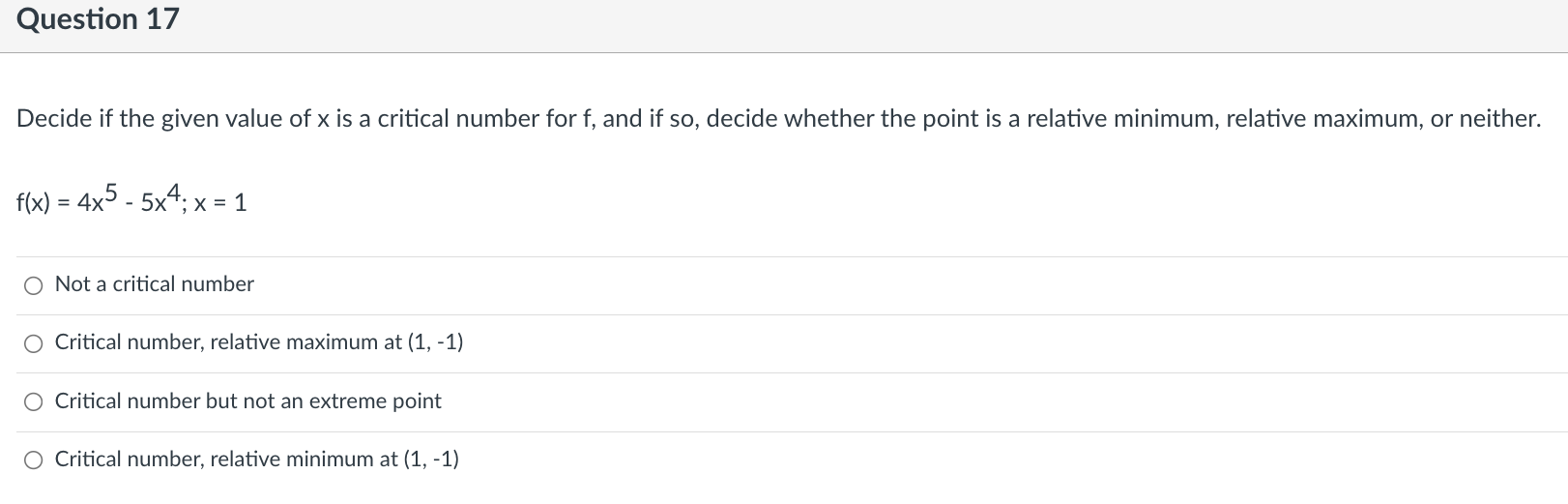
Question 9 Find the indicated derivative of the function. f"'(x} of f(x) = 6x3 + 4x2 - 5x 0 36 o 36x+18 o 18x +36 018 Question 10 Find the open interval(s) where the function is changing as requested. Increasing; y = 7x - 5 O (-5, a\") O (-5, 7) O (4'57) 0 (-00, 0) Question 11 Suppose that the function with the given graph is not f(x), but f'(x). Find the open intervals where f(x) is increasing or decreasing as indicated. Increasing 4+ 3+ 2+ 3 4 5 35 -1+ -2- O (2, 00) O (-00, - 2), (2, 00) O (-2, 2) O (0, 00)Question 12 Find the largest open intervals where the function is concave upward. f (x) = - X x2 + 1 O (-00, - 1) O (1/3, 00) O (-00, -1), (-1, 00 ) O NoneQuestion 13 Find the open intervals where the function is concave upward or concave downward. Find any inflection points. -2 - O Concave upward on (-2, co); concave downward on (co, -2); inflection point at (-2, 2) O Concave upward on (-2, co); concave downward on (-wo, -2); no inflection points O Concave upward on (-co, -2); concave downward on (-2, co); no inflection points O Concave upward on (-co, -2); concave downward on (-2, co); inflection point at (-2, 2)\fQuestion 15 Use I'Hopital's Rule to evaluate the limit. x sin (x->co) is under (lim) (4/x) Jim Xyoo X Sin 4 O (1/4) OO O 1\fQuestion 17 Decide if the given value of X is a critical number for f, and if so, decide whether the point is a relative minimum, relative maximum, or neither. fix) = 4x5 - 5x4; x = 1 0 Not a critical number 0 Critical number, relative maximum at (1, 1) 0 Critical number but not an extreme point 0 Critical number, relative minimum at (1, -1)