Question about weighted quick-union.

Two questions about this answer:

1.Why is it log10^9 instead 10* log10^9?

2.Why does it include 5 comparing parents (why 5?) when doing the union operation?

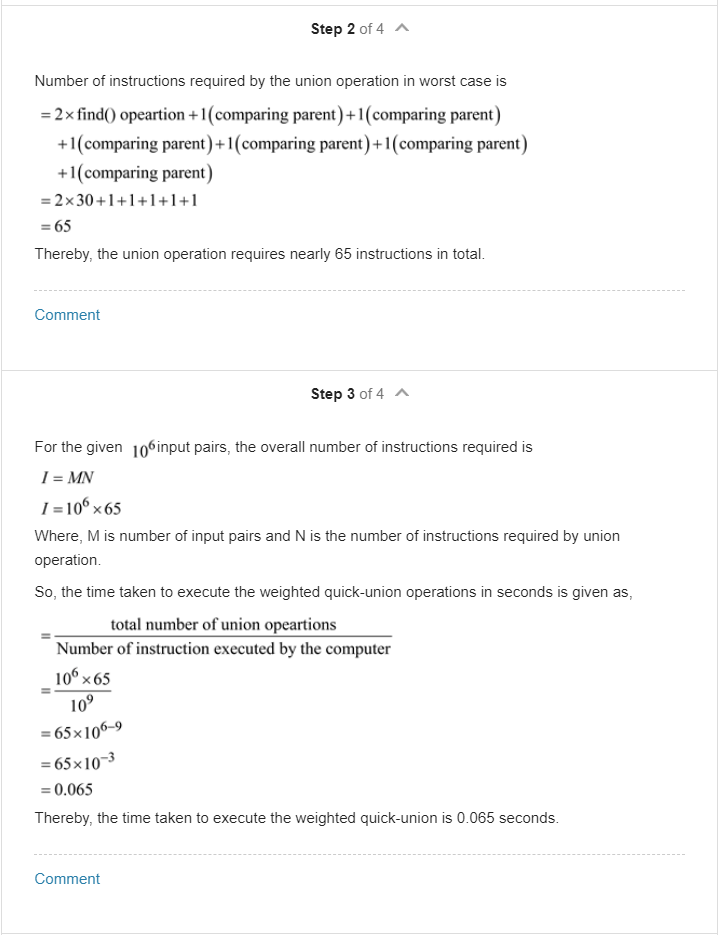
Repeat exercise for weighted quick-union. Exercise Estimate the minimum amount of time (in days) that would be required for quick-find to solve a dynamic connectivity problem with 109 sites and 106 input pairs, on a computer capable of executing 109 instructions per second. Assume that each iteration of the inner for loop requires 10 machine instructions. Step-by-step solution Step 1 of 4 A The weighted quick-union algorithm with N sites uses at most lg N instructions to solve a connectivity problem Given that Number of sites = 10 0 Number of input pairs = 106 o For every second computer can execute 109 instructions. As per the weighted quick-union algorithm, Number of instructions are required for object initialization is -10%. Number of instructions required by the find operation in worst case is Ig(Number of sites). Substitute the value 10% lg(Number of sites ) = 19(109) = 29.8973 230 Thereby, find operation requires nearly 30 instructions. Comment Step 2 of 4 A Number of instructions required by the union operation in worst case is = 2x find() opeartion +1(comparing parent) +1(comparing parent) +1(comparing parent) +1(comparing parent)+1(comparing parent) +1(comparing parent) = 2 x 30+1+1+1+1+1 = 65 Thereby, the union operation requires nearly 65 instructions in total. Comment Step 3 of 4 A For the given 106 input pairs, the overall number of instructions required is I = MN 1 = 10665 Where, M is number of input pairs and N is the number of instructions required by union operation So, the time taken to execute the weighted quick-union operations in seconds is given as, total number of union opeartions Number of instruction executed by the computer 100x65 10 = 65x106-9 = 65x10-3 = 0.065 Thereby, the time taken to execute the weighted quick-union is 0.065 seconds. Comment Step 4 of 4 A Convert the obtained time into days as follows: time taken to execute the weighted quick union Number of minutes 60 0.065 sec 60 = 0.0010 mins Number of minutes Number of hours 60 0.0010 mins 60 =0.0000180hrs Number of hours Number of days 24 0.0000180hrs 24 =0.00000075 days Therefore, the minimum amount of time(in days) required by the weighted quick-union for the given 109 sites and 106 input pairs with computer capacity of execution of 10 instructions per second is 0.00000075 days. Comment