Question: question below: Determine whether a conclusion can be drawn about the existence of uniqueness of a solution of the differential equation (1 - t)y +
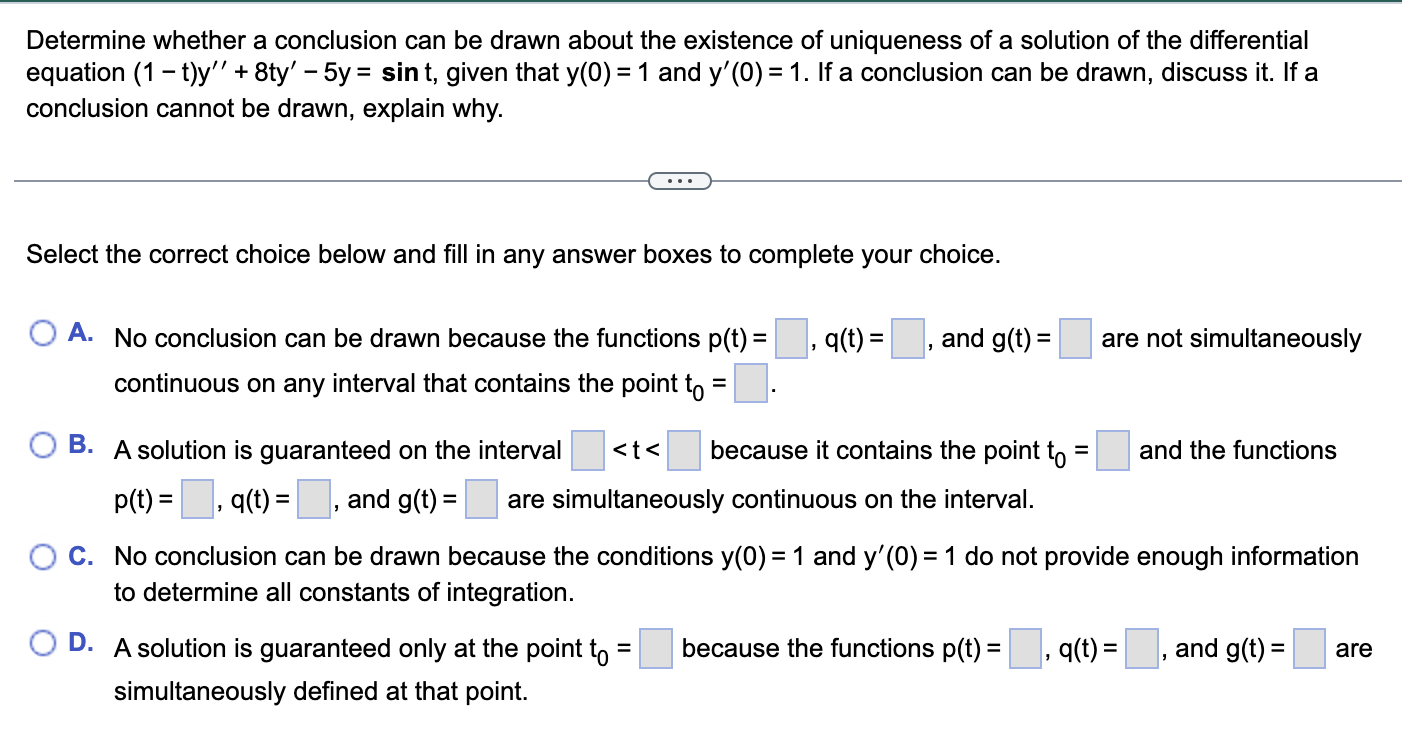

question below:
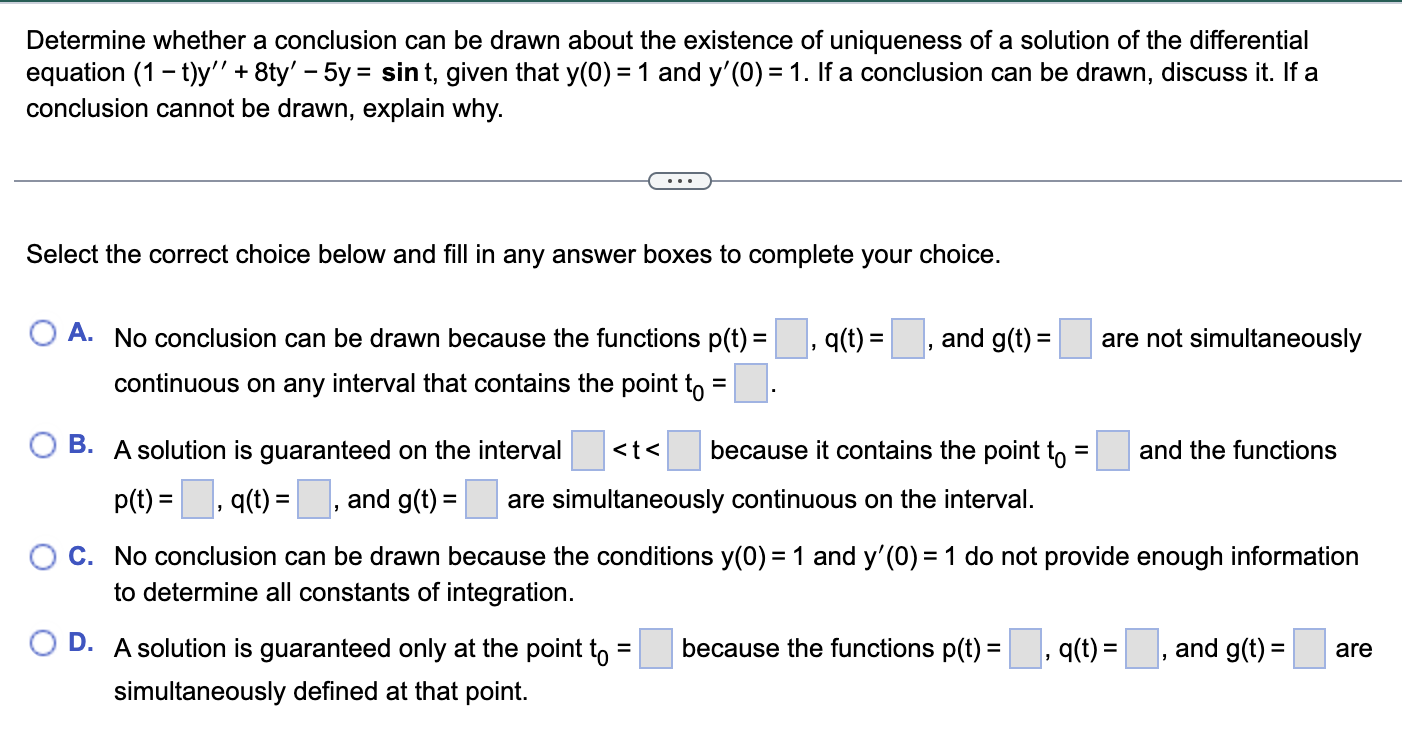

Determine whether a conclusion can be drawn about the existence of uniqueness of a solution of the differential equation (1 - t)y" + 8ty' - 5y = sin t, given that y(0) = 1 and y'(0) = 1. If a conclusion can be drawn, discuss it. If a conclusion cannot be drawn, explain why. . . . Select the correct choice below and fill in any answer boxes to complete your choice. O A. No conclusion can be drawn because the functions p(t) = , q(t) = , and g(t) = are not simultaneously continuous on any interval that contains the point to = O B. A solution is guaranteed on the interval
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


