Question:

Buses arrive at a bus station with i.i.d. interarrival times following an exponential distribution with intensity ?. Alice arrives at the bus station at a deterministic time t. a. (4pts) What is the expected waiting time for Alice until next bus comes? b. (6pts) Let ? be the time when the last bus arrived before time t. Show that t ? ? follows an exponential distribution with parameter ?. c. (6pts) Show that the expected interarrival time between the last bus which arrived before time t and the first bus which arrives after time t is 2 ? . Explain why it is different from the general expected interarrival time 1 ? .

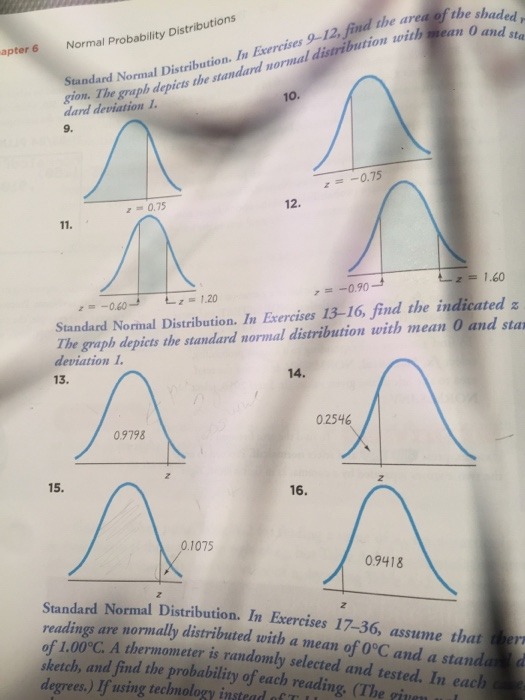
4.7 a) Prove that if A and B are two disjoint events of positive probability in a sample space S, then the conditional probability of one of these events given the other is zero. b) What is the conditional probability of A given B if A C B? c) What is the conditional probability of A given B if B C A?6. Find cov(X, Y) for the following bivariate distribution, you might need cov ( X, Y ) = E(XY ) - UXHY. Please note: ALL working MUST be shown! f (x, y) = 2x if 0 =-0.90- Standard Normal Distribution. In Exercises 13-16, find the indicated & The graph depicts the standard normal distribution with mean O and sta deviation I. 13. 14. 0.9798 0.2546 15. 16. 0.1075 0.9418 Standard Normal Distribution. In Exercises 17-36, assume that ther readings are normally distributed with a mean of OC and a standard of 1.00 C. A thermometer is randomly selected and tested. In each sketch, and find the probability of each reading. (The gin degrees.) If using technology instead of