Question content area top

Part $1$

Use geometry$($not Riemann$$ sums$)$ to evaluate the definite integral. Sketch the graph of the$$ integrand, show the region in$$ question, and interpret your result.

Integral from negative $8$ to $9$ left parenthesis negative StartAbsoluteValue x EndAbsoluteValue right parenthesis dx$89($x$)$dx

Question content area bottom

Part $1$

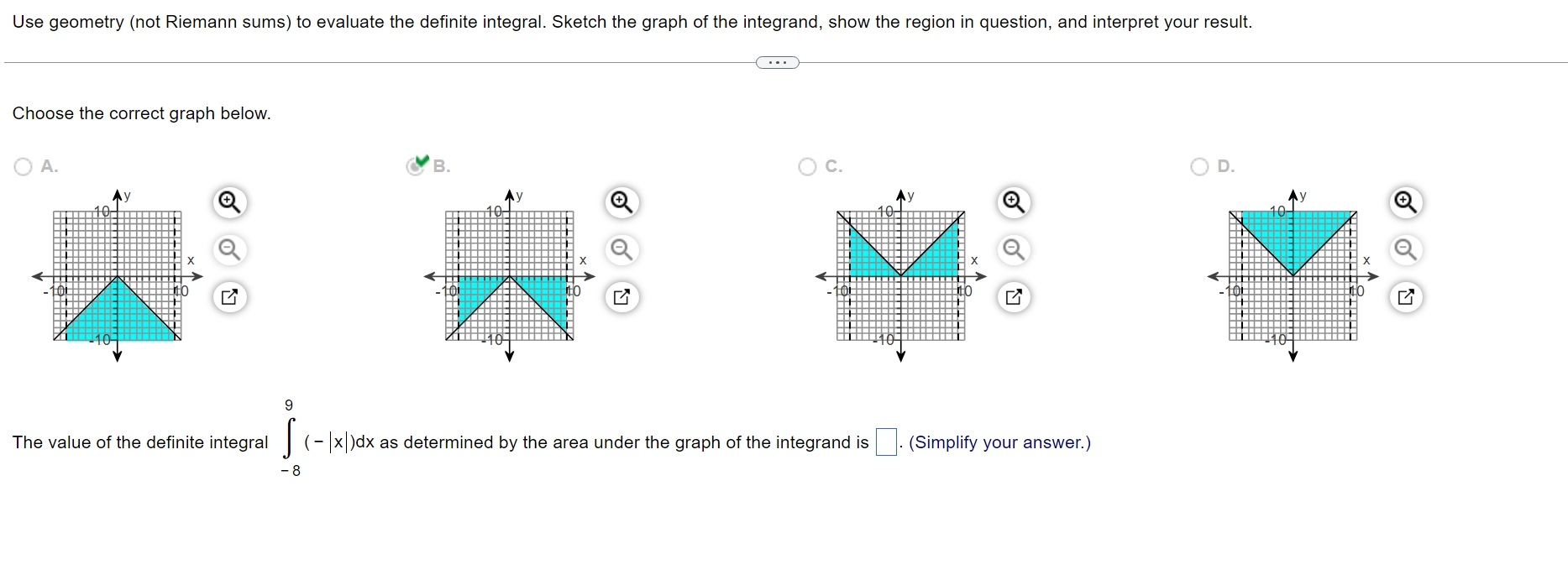
Choose the correct graph below.

A$.$

$-1010-1010$xy

A coordinate system has a horizontal x$-$axis labeled from negative $10$ to $10$ in increments of $1$ and a vertical y$-$axis labeled from negative $10$ to $10$ in increments of $1.$ V$-$shaped graph opens downward from a vertex at $(0,0)$ and passes through $($negative $1,$ negative $1)$ and $(1,$ negative $1).$ A vertical dashed line crosses the x$-$axis at negative $8,$ and another vertical dashed line crosses the x$-$axis at $9.$ The region below the V$-$shaped graph and between the two dashed lines is shaded.

B$.$

$-1010-1010$xy

A coordinate system has a horizontal x$-$axis labeled from negative $10$ to $10$ in increments of $1$ and a vertical y$-$axis labeled from negative $10$ to $10$ in increments of $1.$ V$-$shaped graph opens downward from a vertex at $(0,0)$ and passes through $($negative $1,$ negative $1)$ and $(1,$ negative $1).$ A vertical dashed line crosses the x$-$axis at negative $8,$ and another vertical dashed line crosses the x$-$axis at $9.$ The two regions above the V$-$shaped graph, below the x$-$axis, and between the two dashed lines are shaded.

Your answer is correct.

C$.$

$-1010-1010$xy

A coordinate system has a horizontal x$-$axis labeled from negative $10$ to $10$ in increments of $1$ and a vertical y$-$axis labeled from negative $10$ to $10$ in increments of $1.$ V$-$shaped graph opens upward from a vertex at $(0,0)$ and passes through $($negative $1,1)$ and $(1,1).$ A vertical dashed line crosses the x$-$axis at negative $8,$ and another vertical dashed line crosses the x$-$axis at $9.$ The two regions below the V$-$shaped graph, above the x$-$axis, and between the two dashed lines are shaded.

D$.$

$-1010-1010$xy

A coordinate system has a horizontal x$-$axis labeled from negative $10$ to $10$ in increments of $1$ and a vertical y$-$axis labeled from negative $10$ to $10$ in increments of $1.$ V$-$shaped graph opens upward from a vertex at $(0,0)$ and passes through $($negative $1,1)$ and $(1,1).$ A vertical dashed line crosses the x$-$axis at negative $8,$ and another vertical dashed line crosses the x$-$axis at $9.$ The region above the V$-$shaped graph and between the two dashed lines is shaded.

Part $2$

The value of the definite integral

Integral from negative $8$ to $9$ left parenthesis negative StartAbsoluteValue x EndAbsoluteValue right parenthesis dx$89($x$)$dx

as determined by the area under the graph of the integrand is

enter your response here.

$($Simplify your$$ answer.$)$ Use geometry $($not Riemann sums$)$ to evaluate the definite integral. Sketch the graph of the integrand, show the region in question, and interpret your result.

Choose the correct graph below.

A$.$B$.$

c$.$

D$.$

The value of the definite integral $\backslash (\backslash$int$\_\{-8\}^\{9\}(-|$x$|)\backslash$mathrm$\{$dx$\}\backslash )$ as determined by the area under the graph of the integrand is $.($Simplify your answer.$)$