question d only

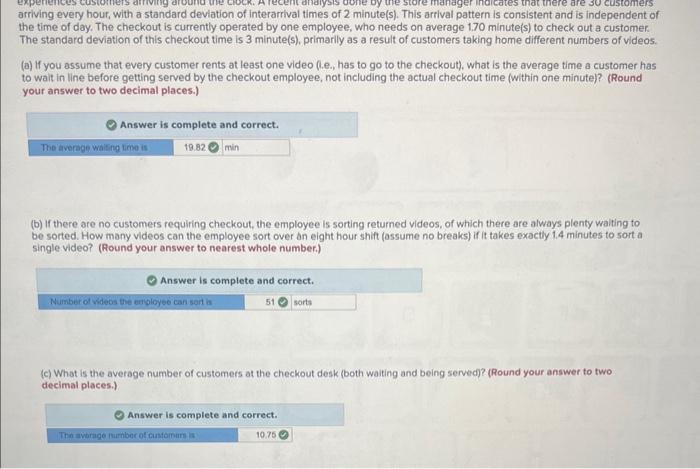
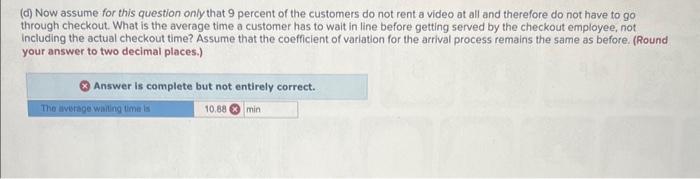
arriving every hour, with a standard deviation of interarrival times of 2 minute(s). This arrival pattern is consistent and is independent of the time of day. The checkout is currently operated by one employee, who needs on average 1.70 minute(s) to check out a customer. The standard deviation of this checkout time is 3 minute(s), primarily as a result of customers taking home different numbers of videos. (a) If you assume that every customer rents at least one video (l.e., has to go to the checkout), what is the average time a customer has to wait in line before getting served by the checkout employee, not including the actual checkout time (within one minute)? (Round your answer to two decimal places.) (b) If there are no customers requiring checkout, the employee is sorting retumed videos, of which there are always plenty walting to be sorted. How many videos can the employee sort over an eight hour shif (assume no breaks) if it takes exactly 1.4 minutes to sort a single video? (Round your answer to nearest whole number.) Answer is complete and correct. (c) What is the average number of customers at the checkout desk (both waiting and being served)? (Round your answer to two decimal places.) (d) Now assume for this question only that 9 percent of the customers do not rent a video at all and therefore do not have to go through checkout. What is the average time a customer has to wait in line before getting served by the checkout employee, not including the actual checkout time? Assume that the coefficient of variation for the arrival process remains the same as before. (Round your answer to two decimal places.) Answer is complete but not entirely correct