Question : Explain how to treat the Schroedinger equation for electrons in atom, in which details of the used approximations should be summarized.

Reference:

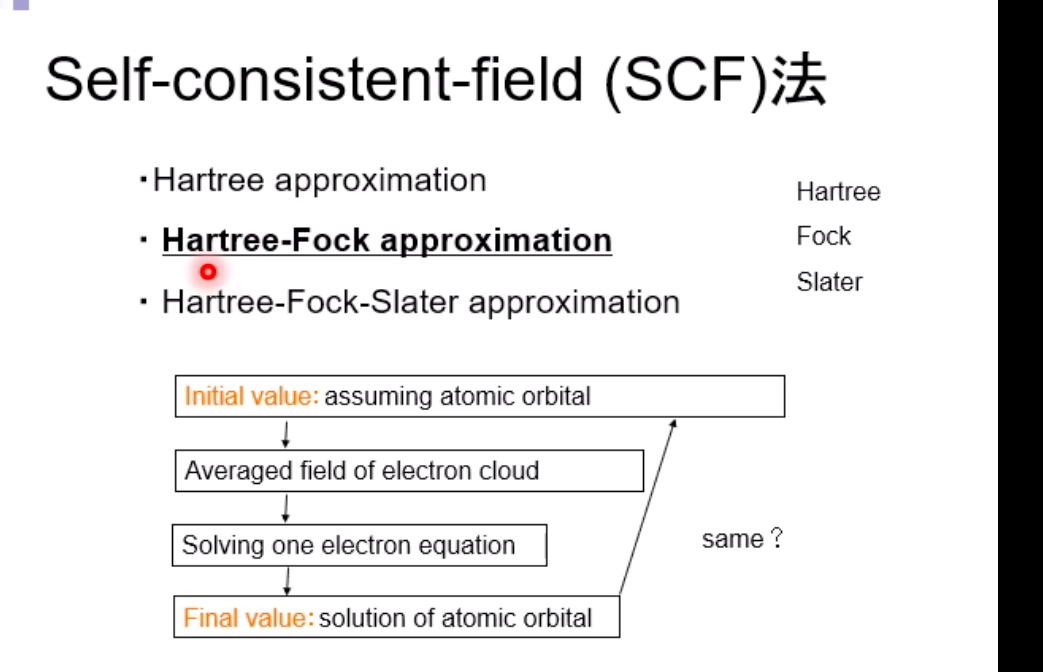
Schrodinger equation for electron in hydrogen atom 1 =V2 + V X = Ex Where x=x(x,yz) , > is a distance from nucleus V Then the Schrodinger equation can be expressed as H V2 X = EXSchrodinger equation for electron in hydrogen atom 1 ) transform the coordinate system from (x,y,z) to (r, 0, ), and separate variables 2) solving radial part equation -Rni(r) 3) solving angular part equation - Yim(q, f) 4) atomic orbital x(r, 0,p)=Rn,I(r) Y im( 0,$)\fAdiabatic approximation ( Born-Oppenheimer approximation ) Schrodinger equation of the system Htotal ustotal _ Ftotalustotal Mass of electron is much lighter than that of nucleus. Melectron = 1/1840 Mproton We neglect motion of nucleus. Hall-elecusall-elec = Fall-elecusall-elec Only the all-electron system without nucleus is considered.Self-consistent-field (SCF); . Hartree approximation Hartree . Hartree-Fock approximation Fock O Slater . Hartree-Fock-Slater approximation Initial value: assuming atomic orbital Averaged field of electron cloud Solving one electron equation same ? Final value: solution of atomic orbitalHartree approximation Each electron moves independently - WFs of all electrons can be expressed by a product of the one electron WFs Y' (1,2, ... , N) = 41(1)42(2) ... 4N(N)Hartree approximation Charge density at position r N N p(r) = > pi(r) = up:(r)]2 E Coulombic repulsion from the electron cloud at ri Vrep (1]) = P(12) dr2 112 The above potential includes the one from oneself ( self-interaction), which should be subtracted, and adding the Potential from nucleus., then we can obtain the potential for one electron of interest. Vi(n])= + P (12) dr2 - Pi(12) dr2 11 112 112Hartree approximation One electron Schrodinger equation for ith electron Z p(12) Pi (12) 112 112 This approximation do not satisfy Pauli's exclusion principle Pauli's exclusion principle More than two electrons do not take same quantum number, i.e., not stay at the same state. . Not more than 1 electron can stay at one orbital. WF should be antisymmetrial when electrons are exchanged.Hatree-Fock approximation O .Assuming electrons move independently in Hartree approximation. .Pauli's exclusion principle is not satisfied. To satisfy Pauli's exclusion principle, WF of the system is expressed by Slater's determinantHatree-Fock approximation Slater's determinant 41(1) 41(12) . 41 (IN) = (N!)-1/2 92(10 42(12) . 42 (IN) . .. IN(1 1) 4N(12) ... ON (IN) From a nature of determinant, 1) if two lines or two column are equivalent, determinant itself is zero, which means two electron cannot occupy the same position at the same time, 2) exchanging subscript cause the sign flip, which means WF is anti- symmetrical in such exchange\f