Question: fill this code

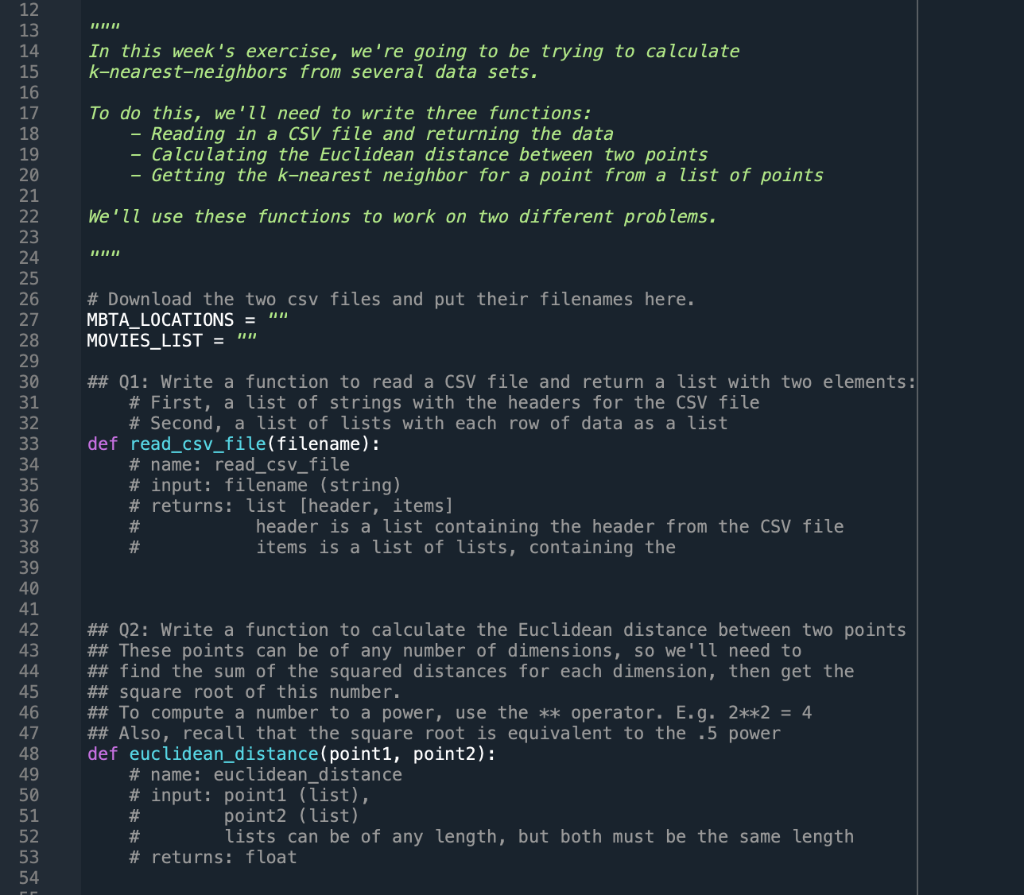
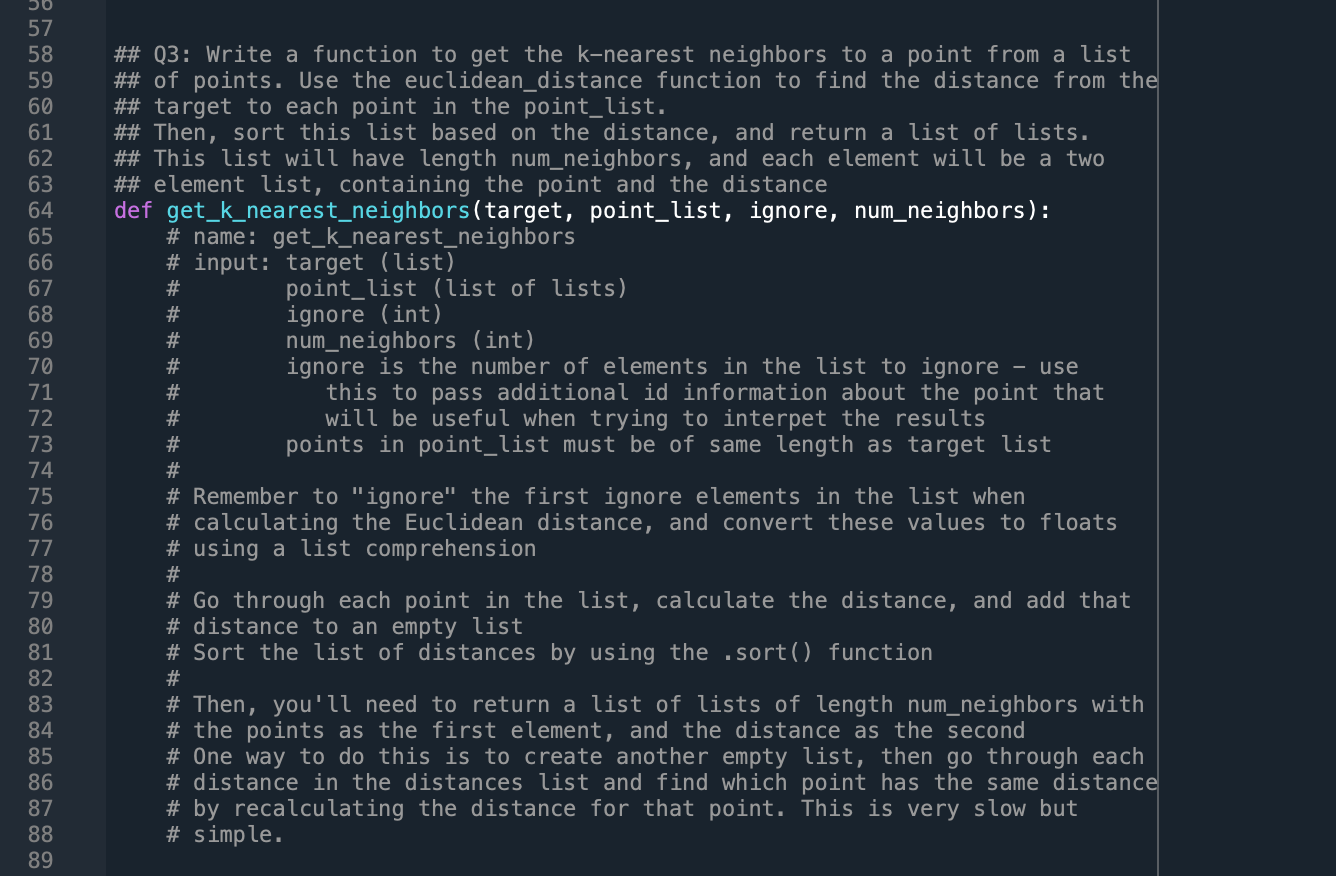
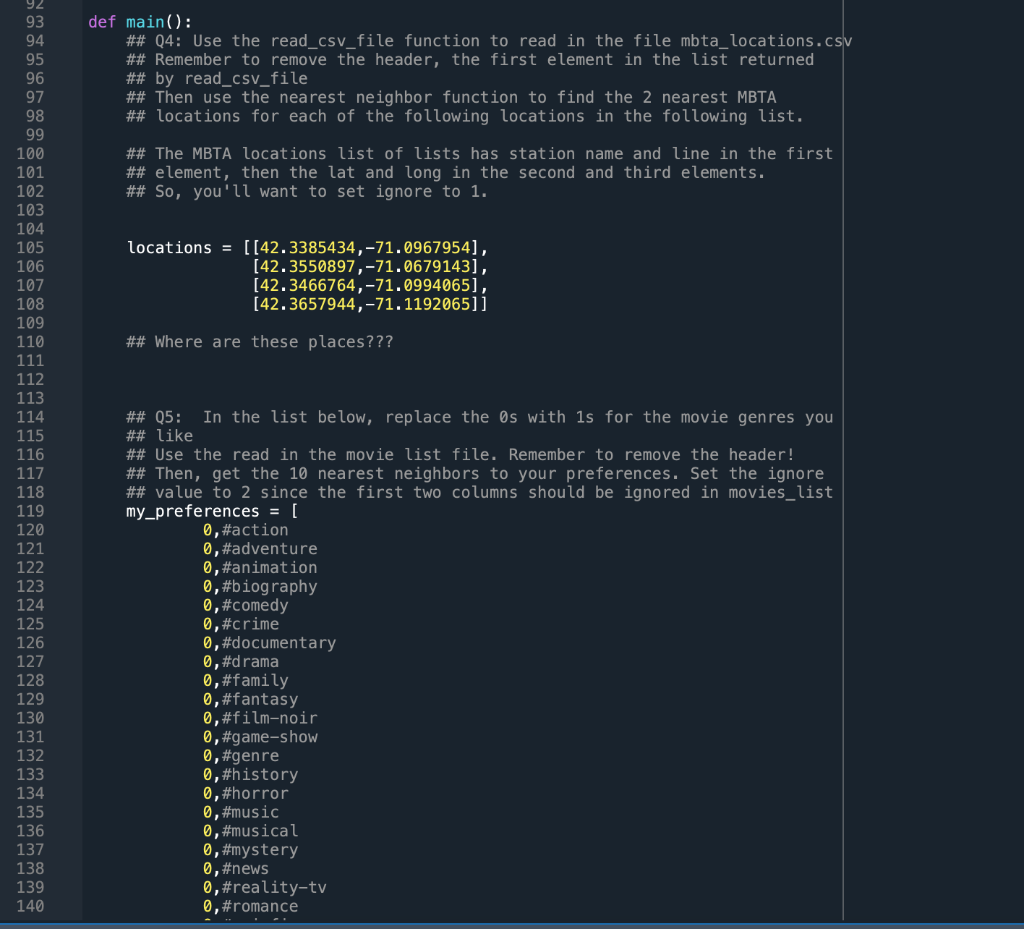
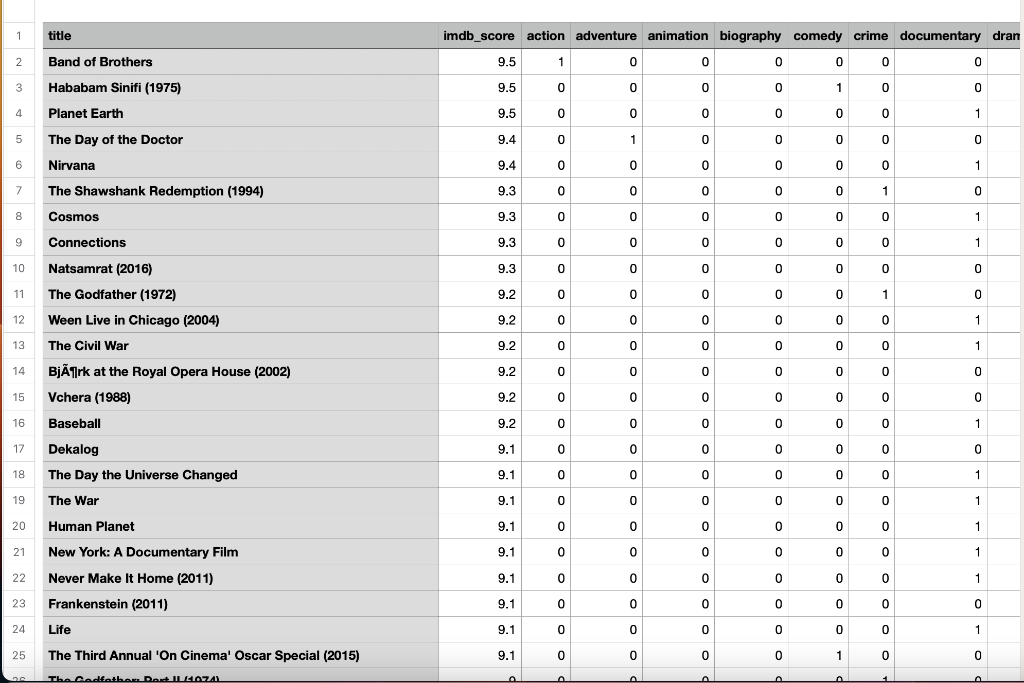
In this week's exercise, we're going to be trying to calculate k-nearest-neighbors from several data sets. To do this, we'll need to write three functions: - Reading in a CSV file and returning the data - Calculating the Euclidean distance between two points - Getting the k-nearest neighbor for a point from a list of points We'll use these functions to work on two different problems. \# Download the two csv files and put their filenames here. MBTA_LOCATIONS =" MOVIESS_LIST =" \# Q1: Write a function to read a CSV file and return a list with two elements \# First, a list of strings with the headers for the CSV file \# Second, a list of lists with each row of data as a list def read_csv_file(filename): \# name: read_csv_file \# input: filename (string) \# returns: list [header, items] \# header is a list containing the header from the CSV file \# items is a list of lists, containing the \#\# Q2: Write a function to calculate the Euclidean distance between two points \#\# These points can be of any number of dimensions, so we'll need to \#\# find the sum of the squared distances for each dimension, then get the \#\# square root of this number. \#\# To compute a number to a power, use the ** operator. E.g. 22=4 \#\# Also, recall that the square root is equivalent to the .5 power def euclidean_distance(point1, point2): \# name: euclidean_distance \# input: point1 ('ist), \# point2 (list) \# lists can be of any length, but both must be the same length \# returns: float \#\# Q3: Write a function to get the k-nearest neighbors to a point from a list \#\# of points. Use the euclidean_distance function to find the distance from the \#\# target to each point in the point_list. \#\# Then, sort this list based on the distance, and return a list of lists. \#\# This list will have length num_neighbors, and each element will be a two \#\# element list, containing the point and the distance def get_k_nearest_neighbors(target, point_list, ignore, num_neighbors): \# name: get_k_nearest_neighbors \# input: target (list) \# point_list (list of lists) \# ignore (int) \# num_neighbors (int) \# ignore is the number of elements in the list to ignore - use \# this to pass additional id information about the point that \# will be useful when trying to interpet the results \# points in point_list must be of same length as target list \# Remember to "ignore" the first ignore elements in the list when \# calculating the Euclidean distance, and convert these values to floats \# using a list comprehension \# Go through each point in the list, calculate the distance, and add that \# distance to an empty list \# Sort the list of distances by using the . sort() function # \# Then, you'll need to return a list of lists of length num_neighbors with \# the points as the first element, and the distance as the second \# One way to do this is to create another empty list, then go through each \# distance in the distances list and find which point has the same distance \# by recalculating the distance for that point. This is very slow but \# simple. mbta_stations In this week's exercise, we're going to be trying to calculate k-nearest-neighbors from several data sets. To do this, we'll need to write three functions: - Reading in a CSV file and returning the data - Calculating the Euclidean distance between two points - Getting the k-nearest neighbor for a point from a list of points We'll use these functions to work on two different problems. \# Download the two csv files and put their filenames here. MBTA_LOCATIONS =" MOVIESS_LIST =" \# Q1: Write a function to read a CSV file and return a list with two elements \# First, a list of strings with the headers for the CSV file \# Second, a list of lists with each row of data as a list def read_csv_file(filename): \# name: read_csv_file \# input: filename (string) \# returns: list [header, items] \# header is a list containing the header from the CSV file \# items is a list of lists, containing the \#\# Q2: Write a function to calculate the Euclidean distance between two points \#\# These points can be of any number of dimensions, so we'll need to \#\# find the sum of the squared distances for each dimension, then get the \#\# square root of this number. \#\# To compute a number to a power, use the ** operator. E.g. 22=4 \#\# Also, recall that the square root is equivalent to the .5 power def euclidean_distance(point1, point2): \# name: euclidean_distance \# input: point1 ('ist), \# point2 (list) \# lists can be of any length, but both must be the same length \# returns: float \#\# Q3: Write a function to get the k-nearest neighbors to a point from a list \#\# of points. Use the euclidean_distance function to find the distance from the \#\# target to each point in the point_list. \#\# Then, sort this list based on the distance, and return a list of lists. \#\# This list will have length num_neighbors, and each element will be a two \#\# element list, containing the point and the distance def get_k_nearest_neighbors(target, point_list, ignore, num_neighbors): \# name: get_k_nearest_neighbors \# input: target (list) \# point_list (list of lists) \# ignore (int) \# num_neighbors (int) \# ignore is the number of elements in the list to ignore - use \# this to pass additional id information about the point that \# will be useful when trying to interpet the results \# points in point_list must be of same length as target list \# Remember to "ignore" the first ignore elements in the list when \# calculating the Euclidean distance, and convert these values to floats \# using a list comprehension \# Go through each point in the list, calculate the distance, and add that \# distance to an empty list \# Sort the list of distances by using the . sort() function # \# Then, you'll need to return a list of lists of length num_neighbors with \# the points as the first element, and the distance as the second \# One way to do this is to create another empty list, then go through each \# distance in the distances list and find which point has the same distance \# by recalculating the distance for that point. This is very slow but \# simple. mbta_stations