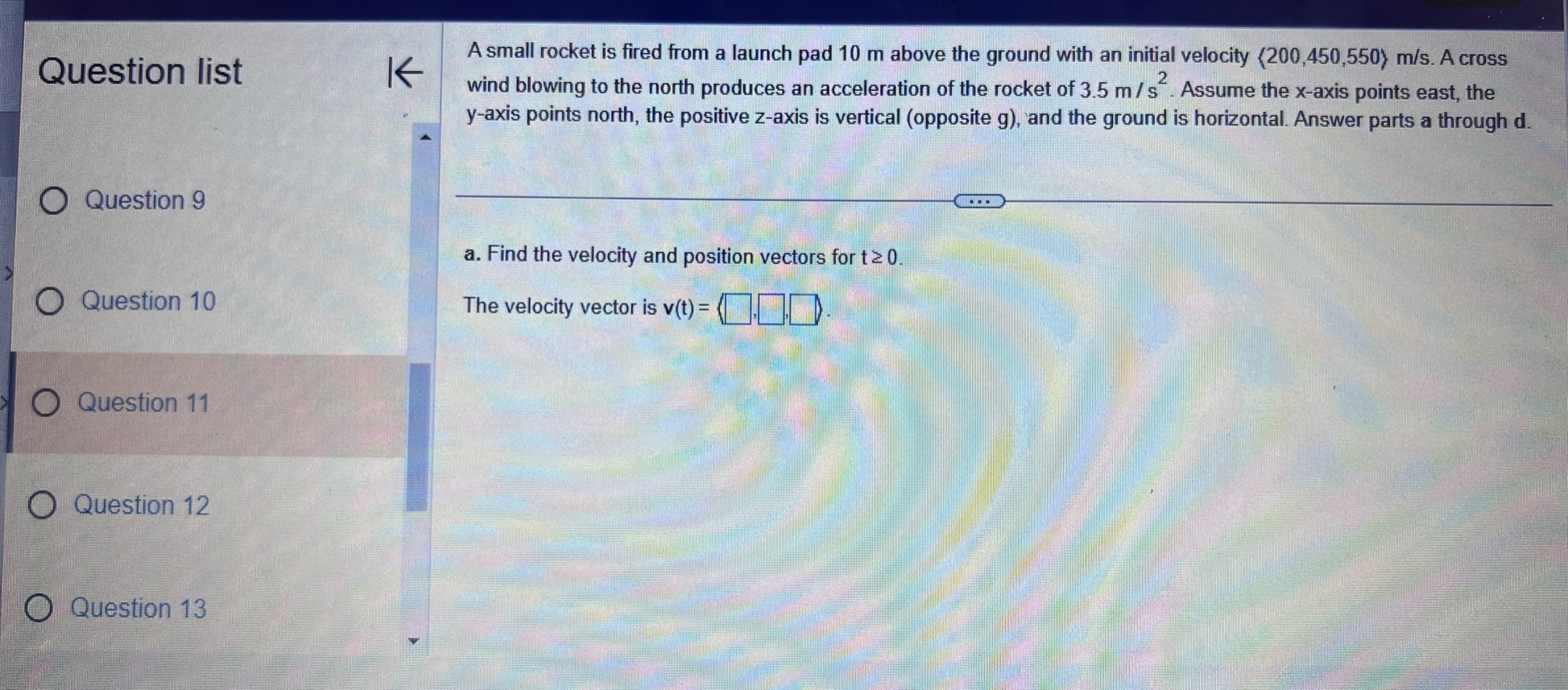
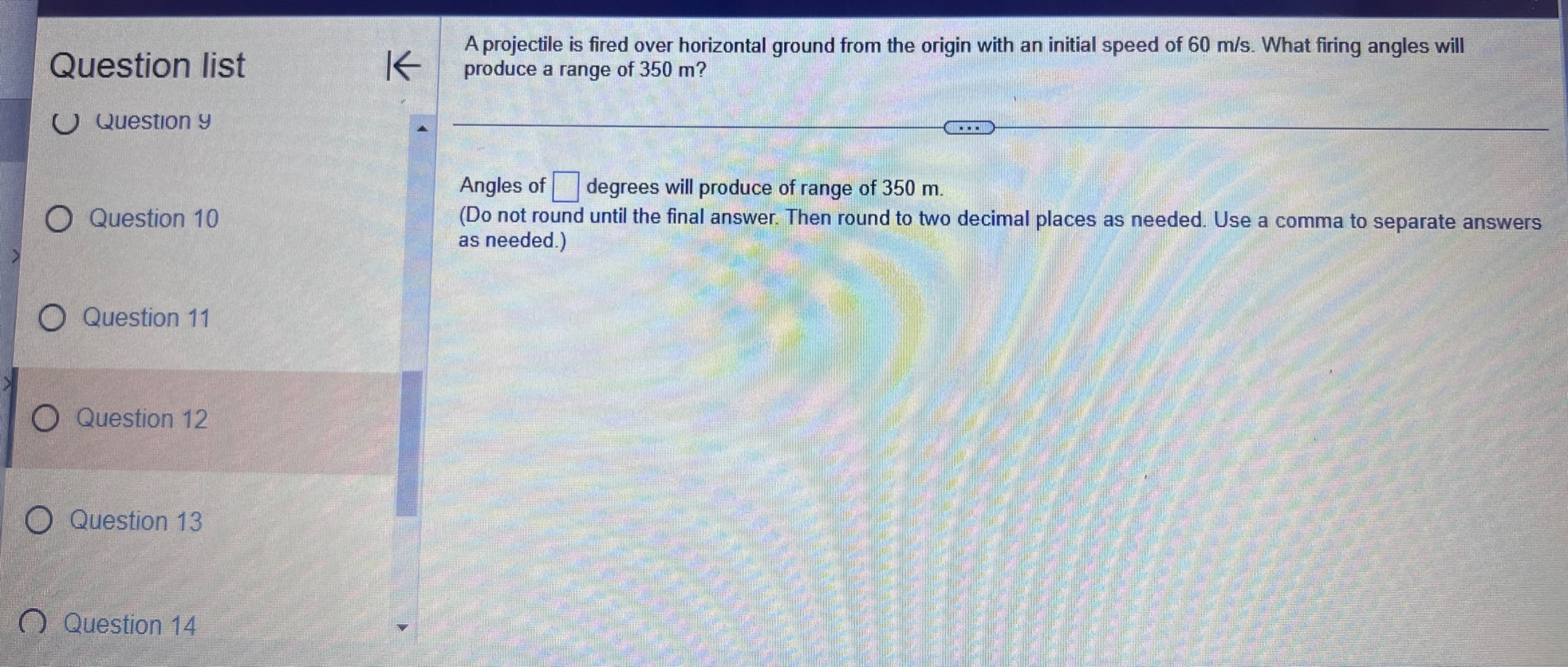
Question: Question list A small rocket is fired from a launch pad 10 m above the ground with an initial velocity (200,450,550) m/s. A cross K
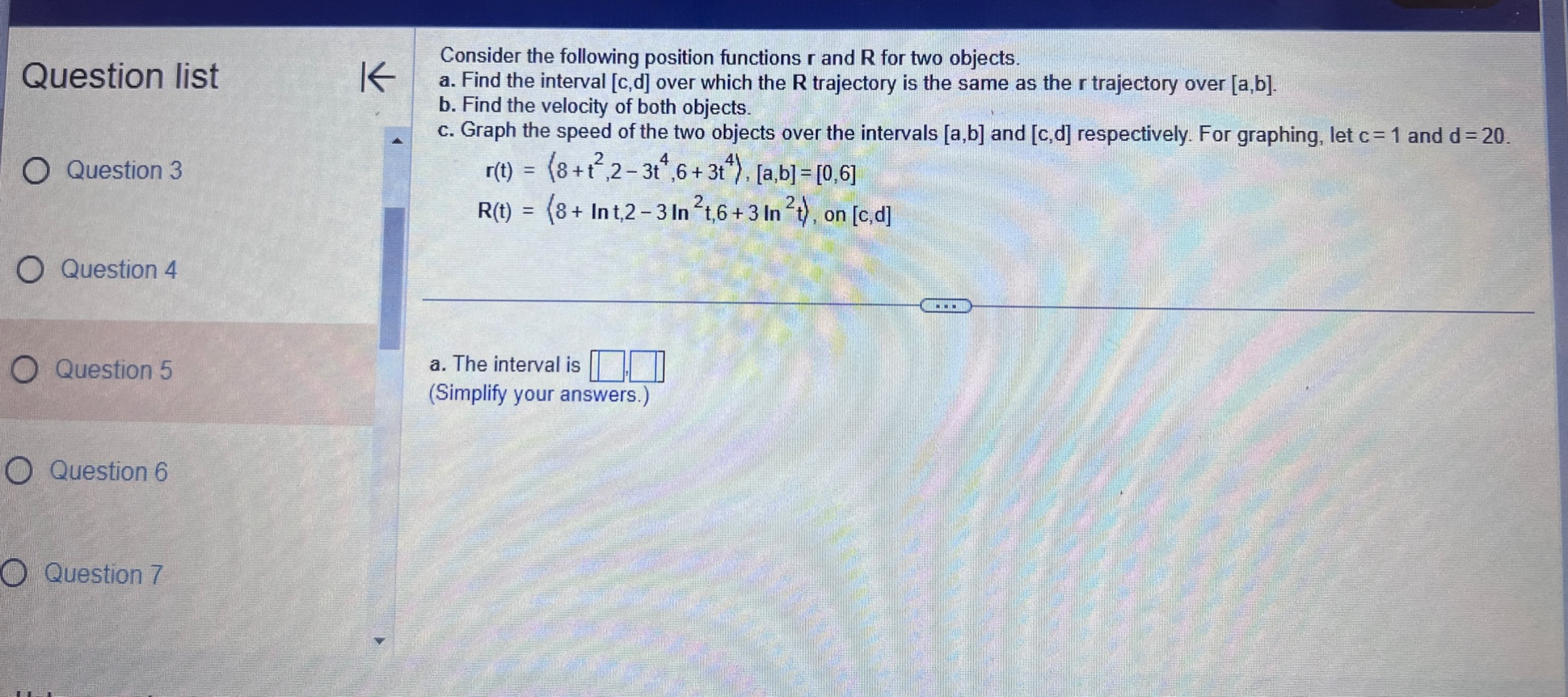



![Find the interval [c,d] over which the R trajectory is the same](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666475f7c1dae_831666475f79ed1f.jpg)
![as the r trajectory over [a, b]. b. Find the velocity of](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666475f82552c_832666475f809b7c.jpg)
![intervals [a,b] and [c,d] respectively. For graphing, let c = 1 and](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666475f904847_832666475f8d61f2.jpg)

![3t ), [a,b] =[0,6] R(t) = (8 + Int,2 - 3 In](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666475f9c61cc_833666475f9a33cf.jpg)
![2t,6 + 3 In 2t), on [c,d] Question 4 Question 5 a.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666475fa33a78_834666475fa16457.jpg)
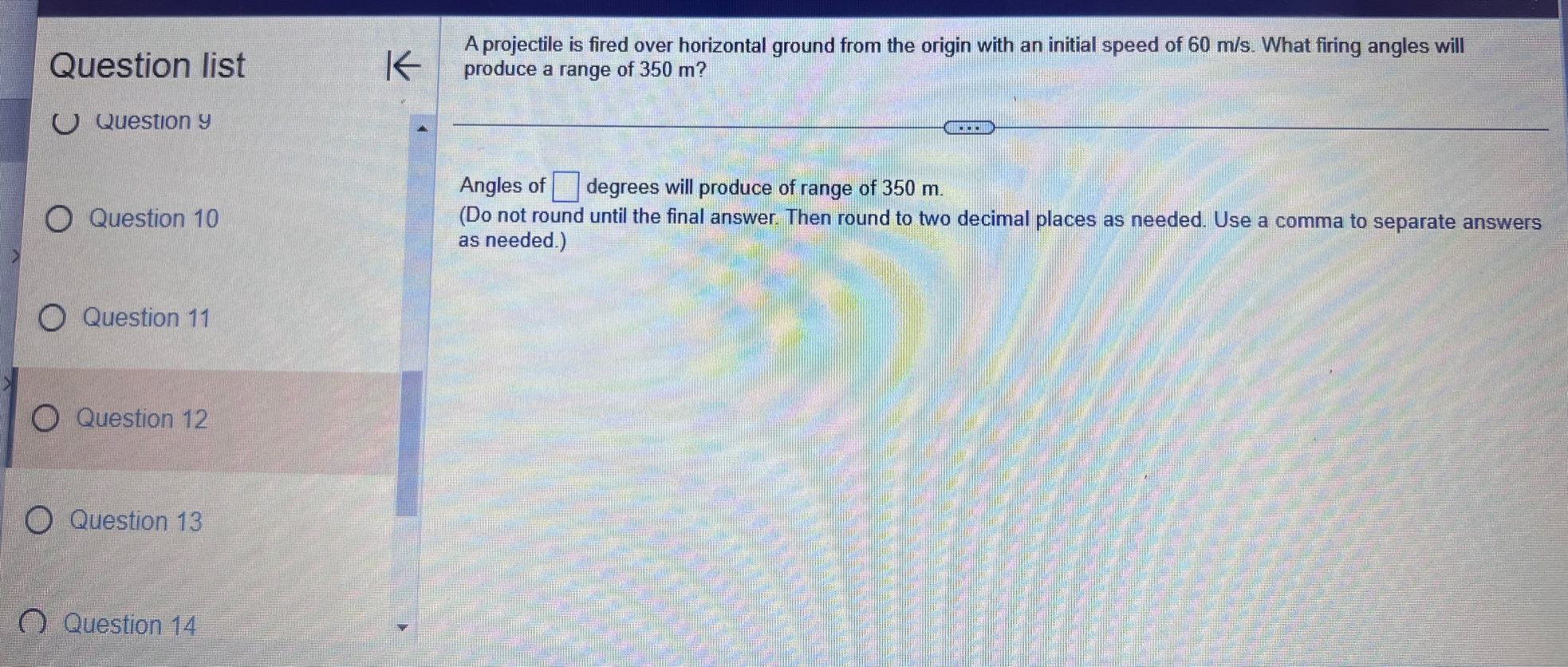
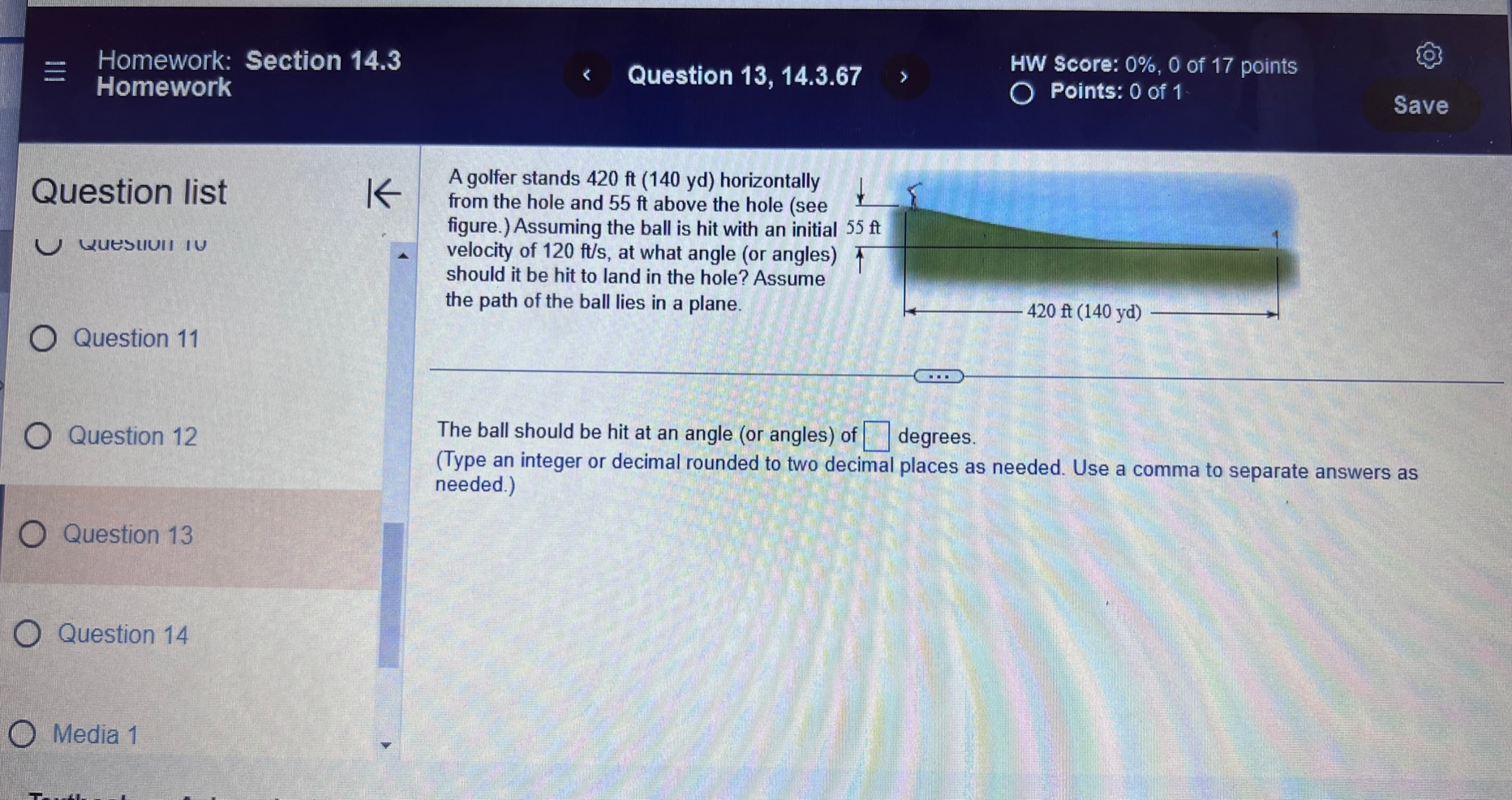
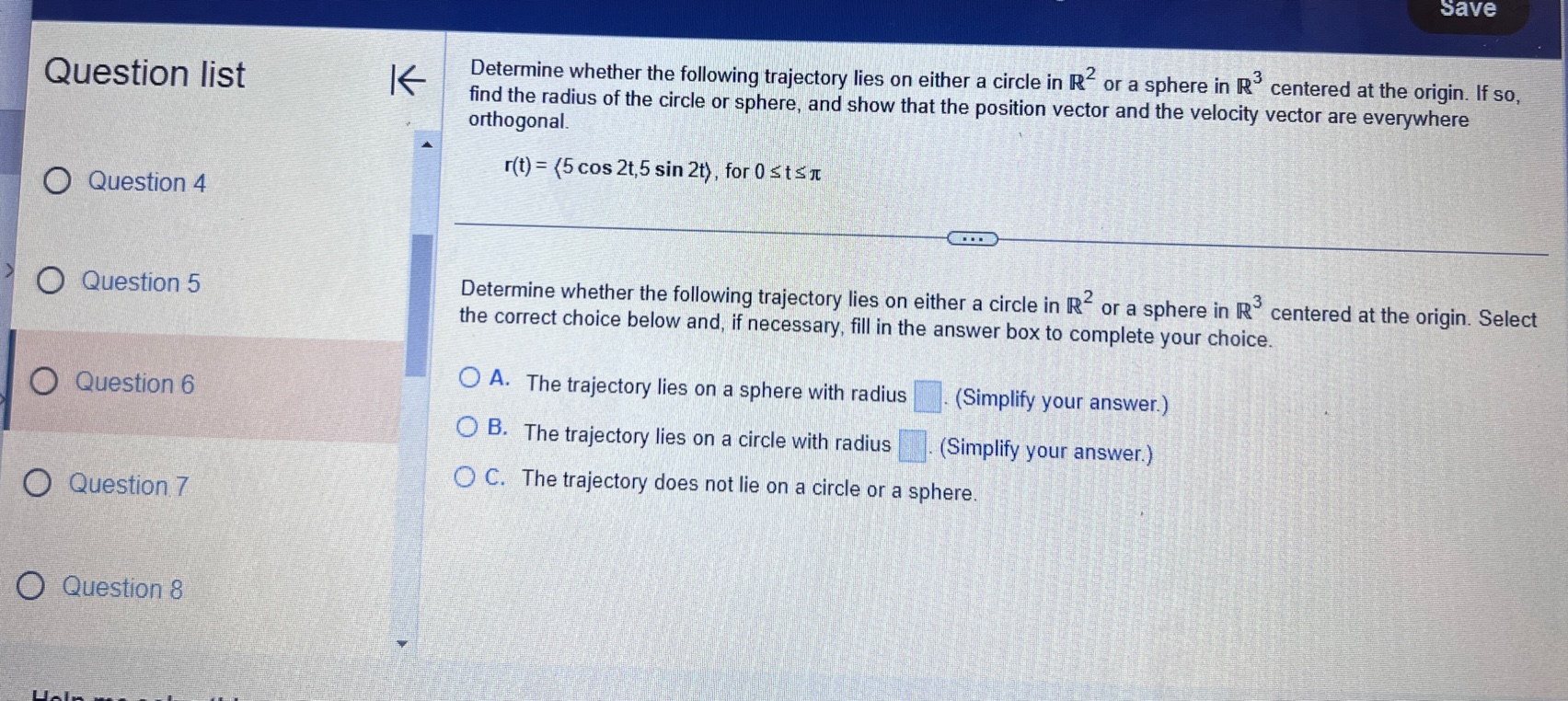

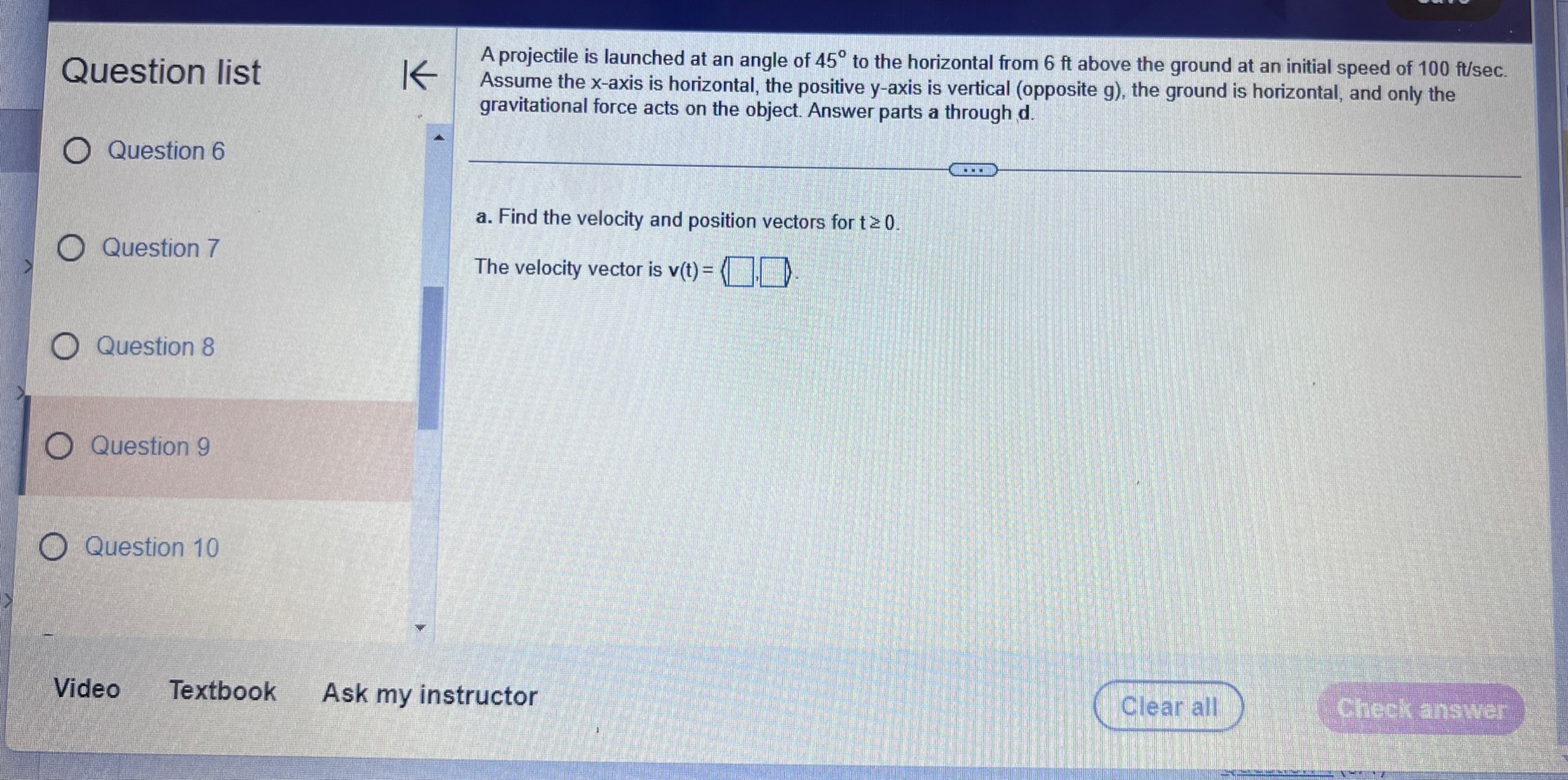
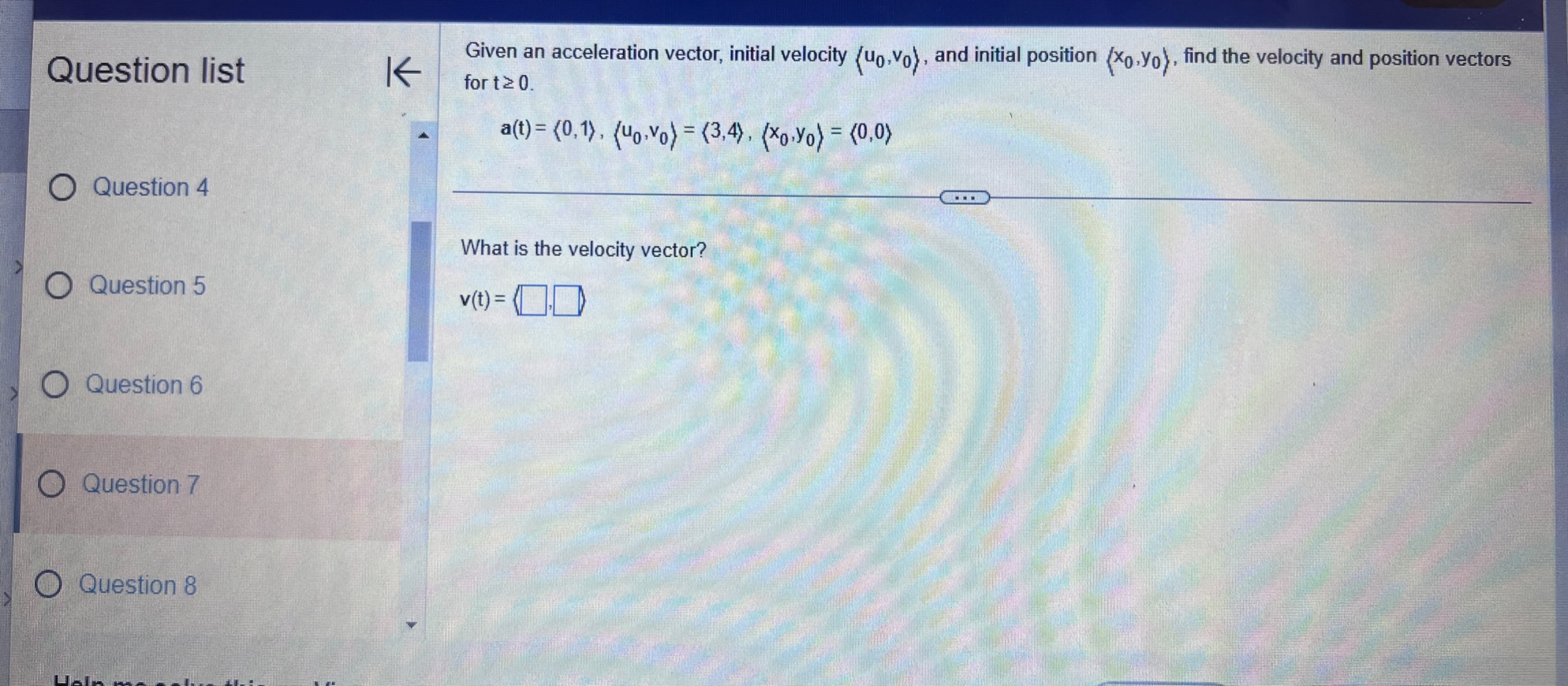
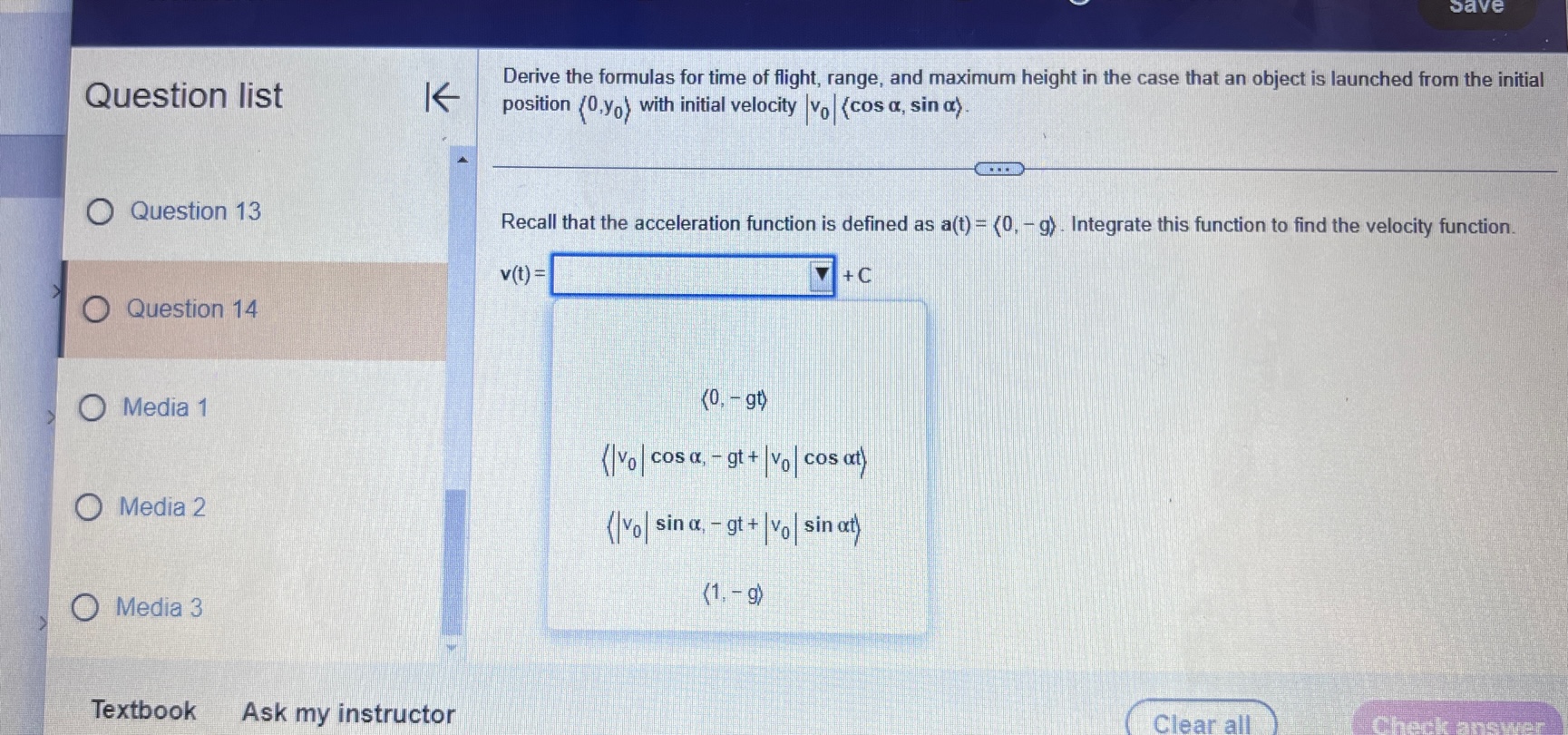
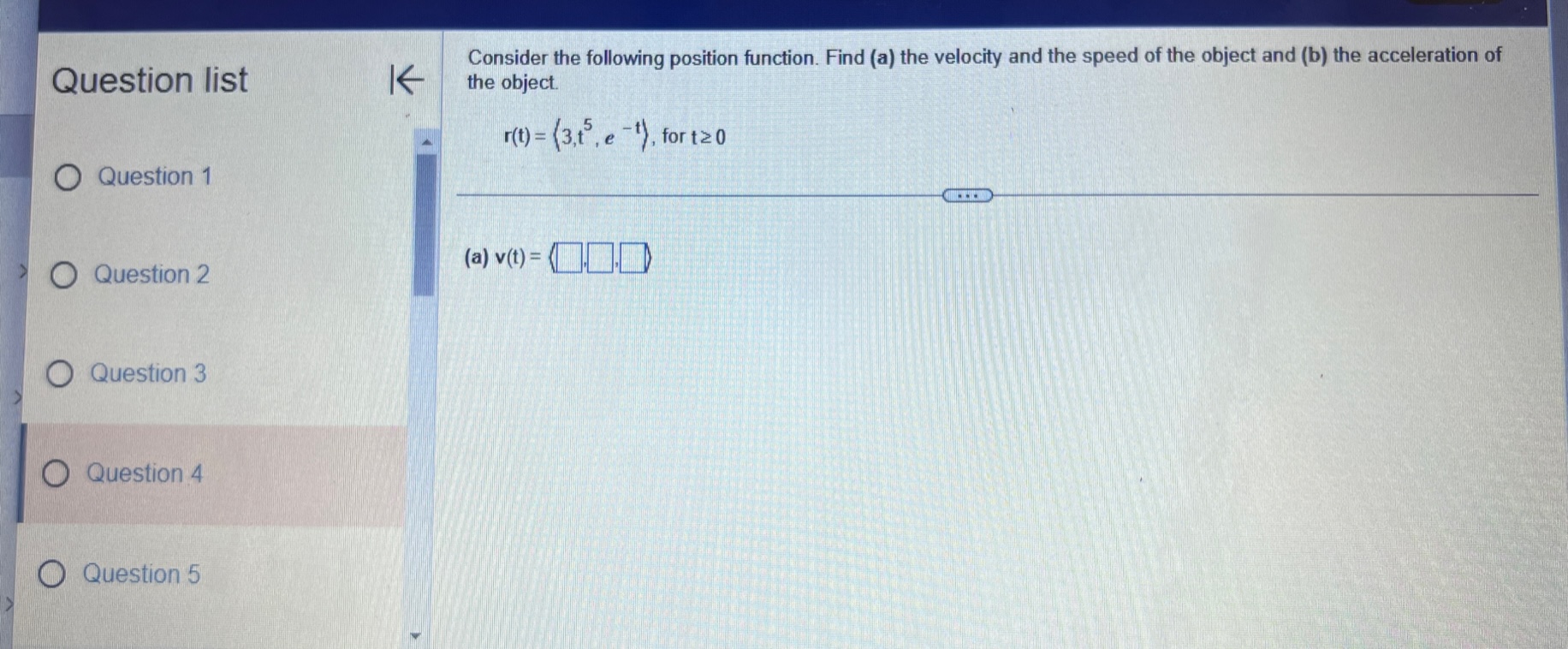
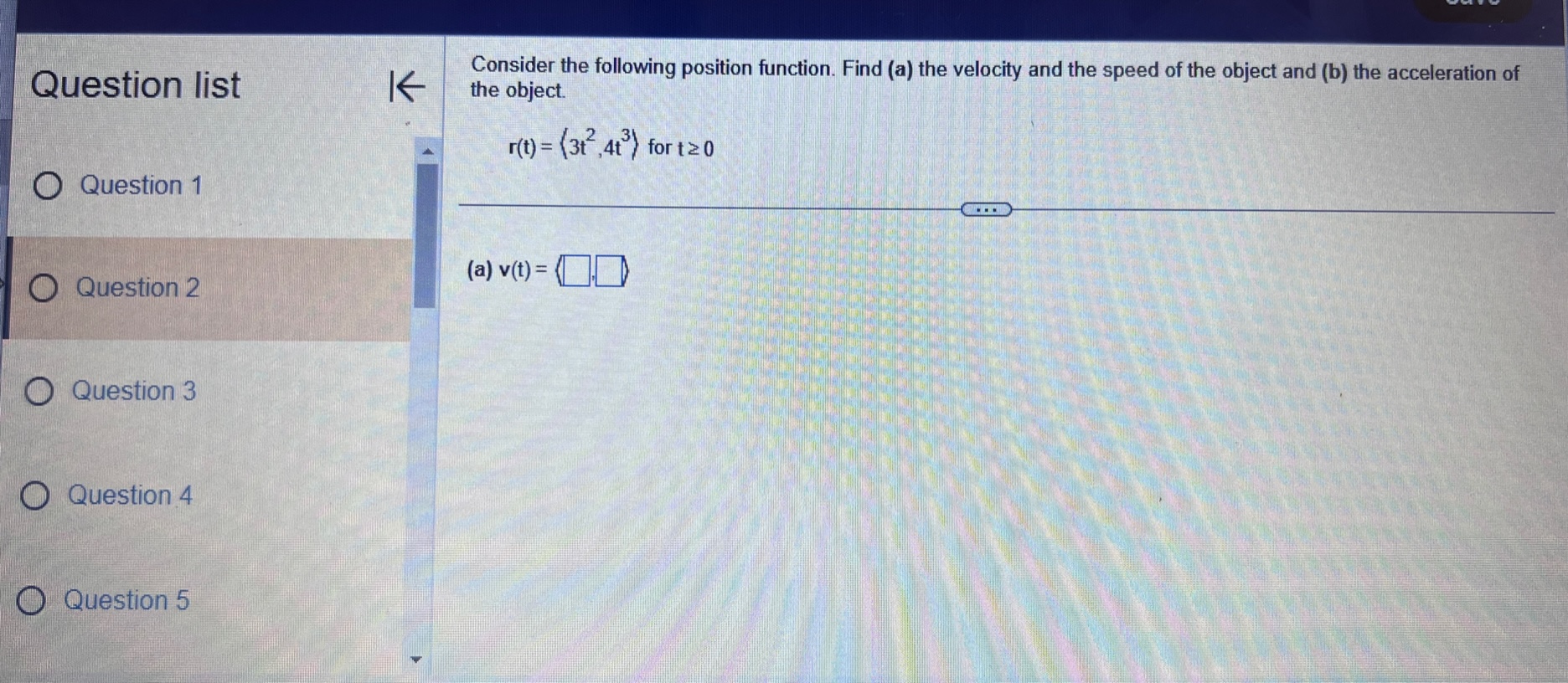
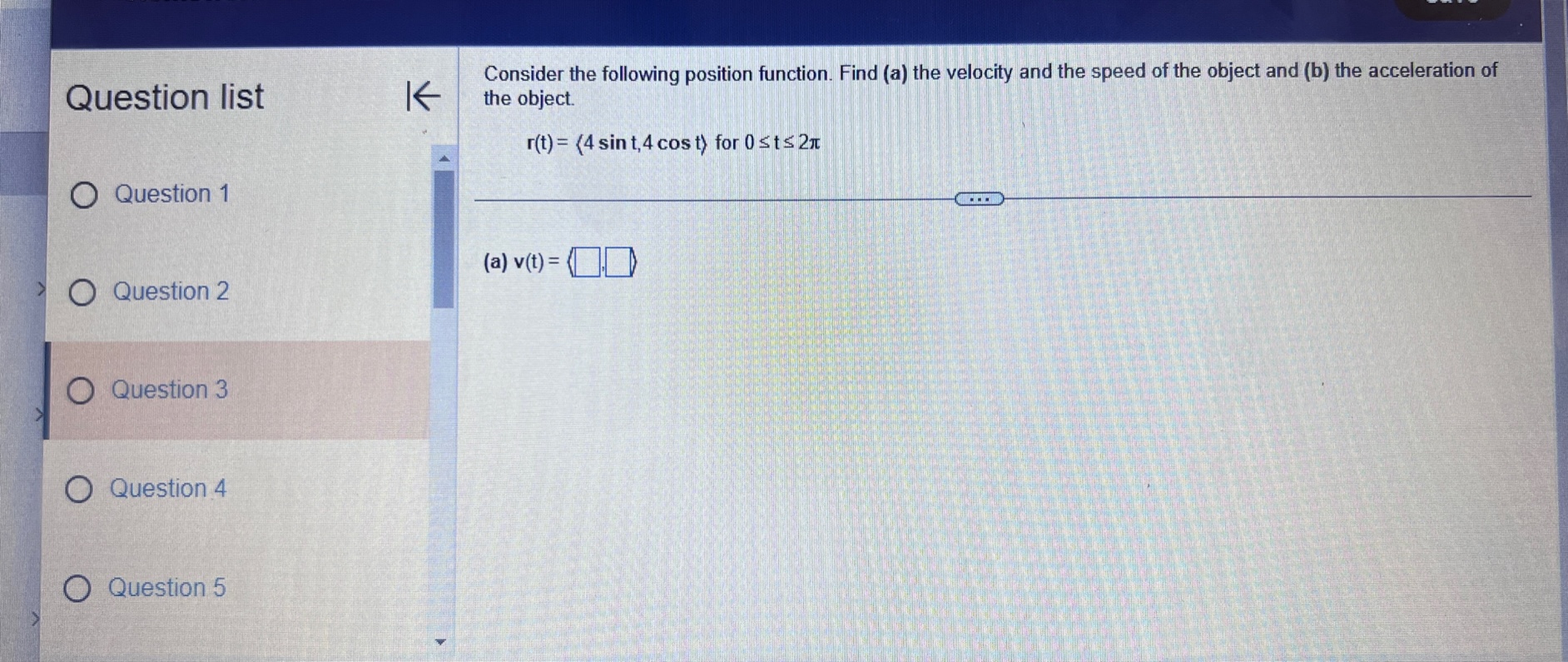
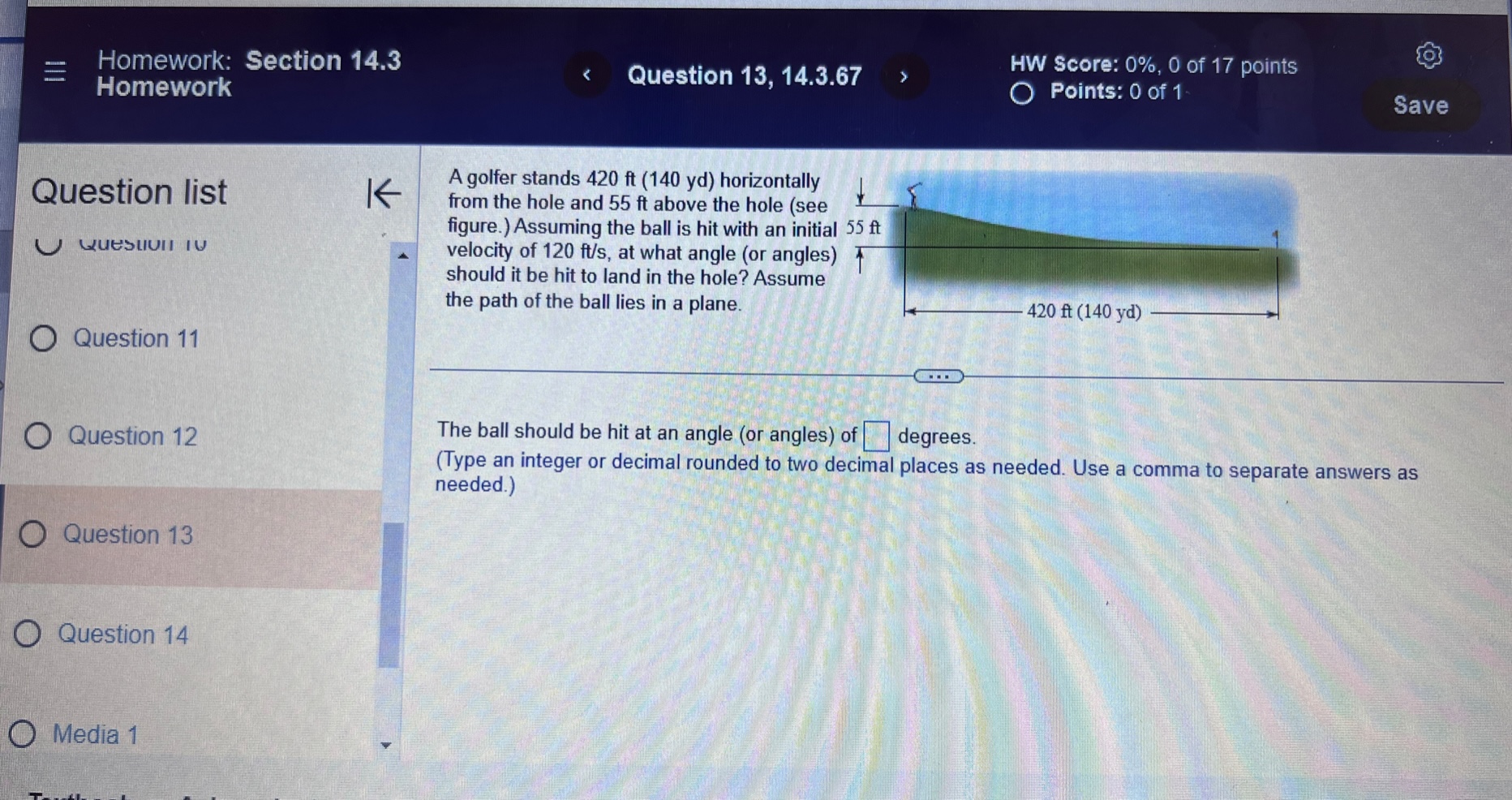
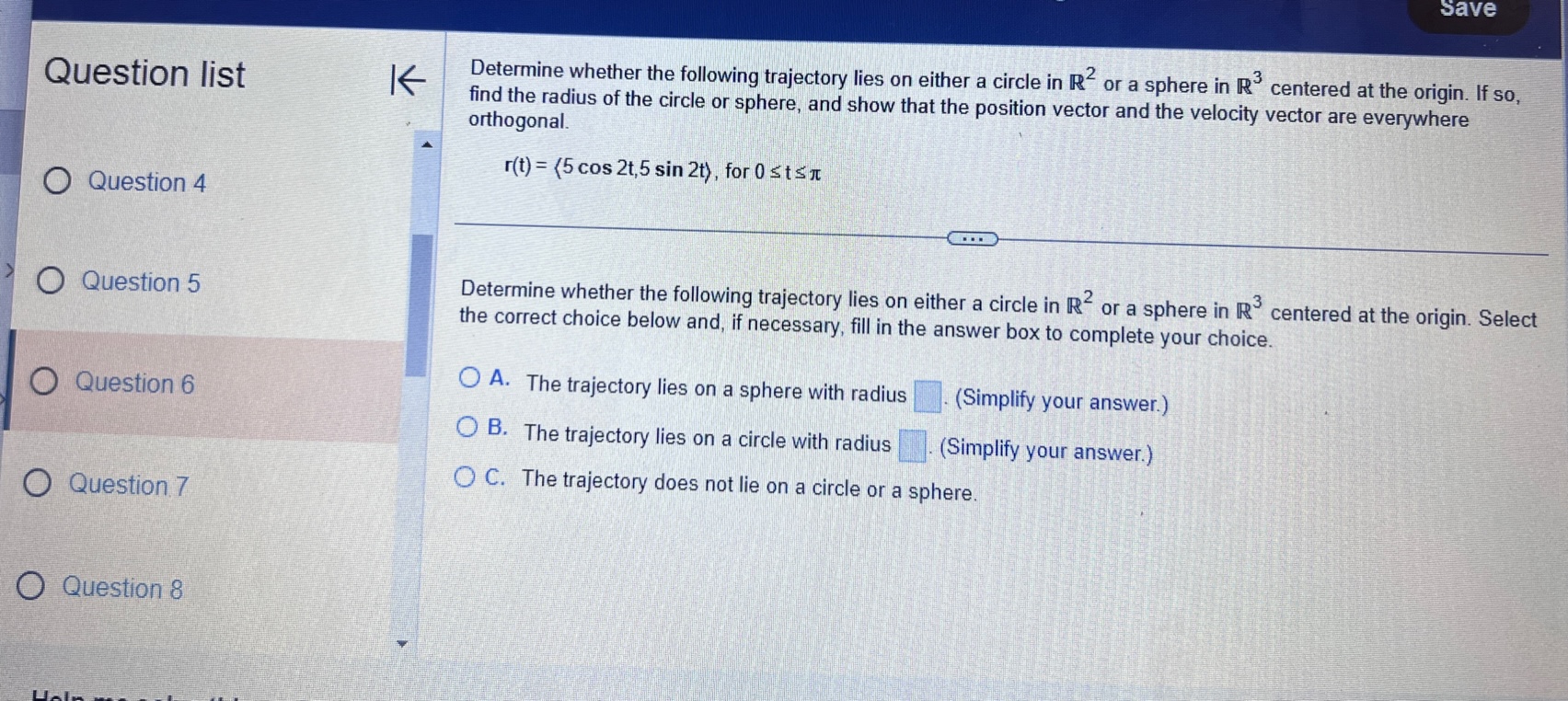
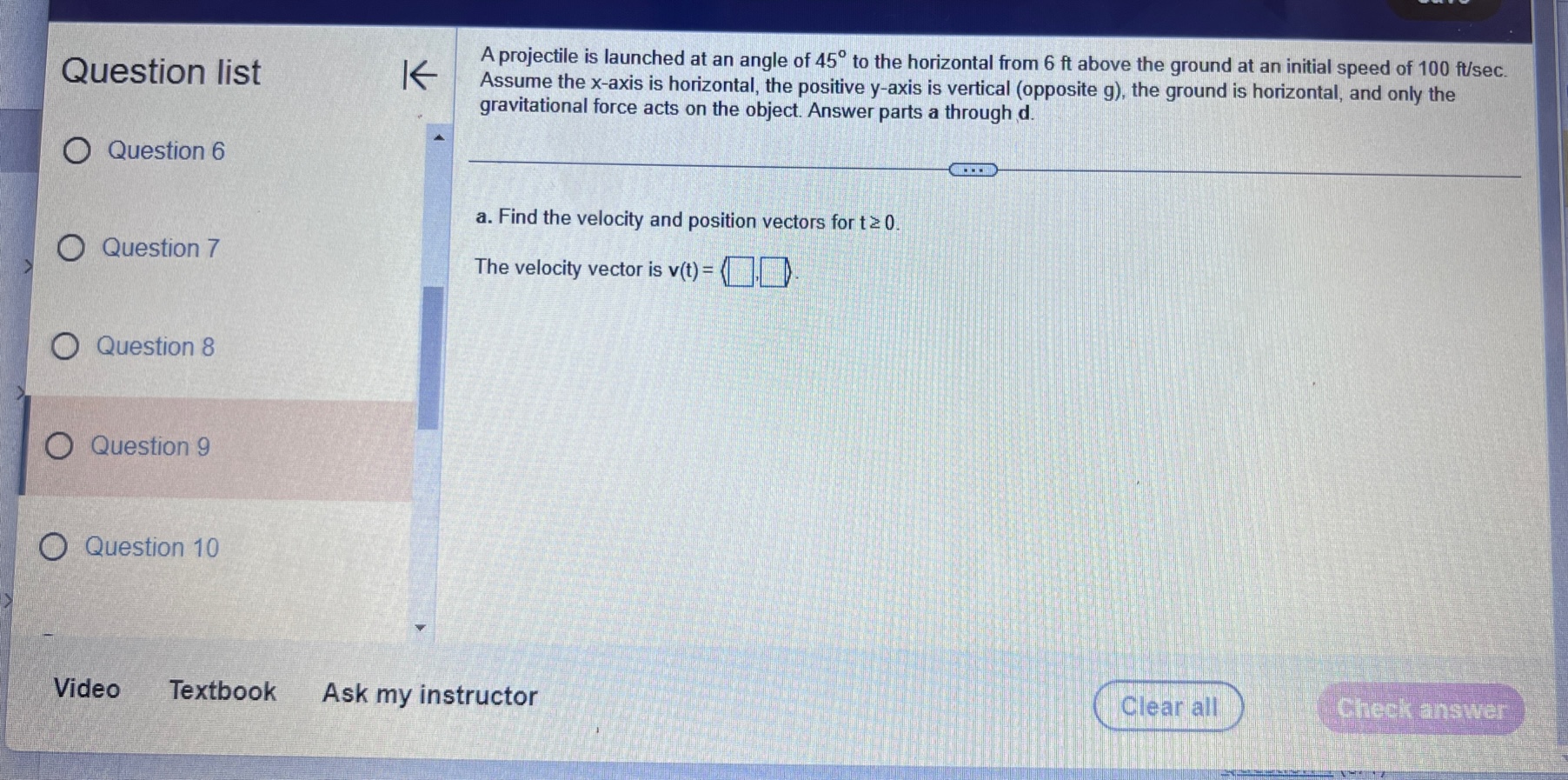
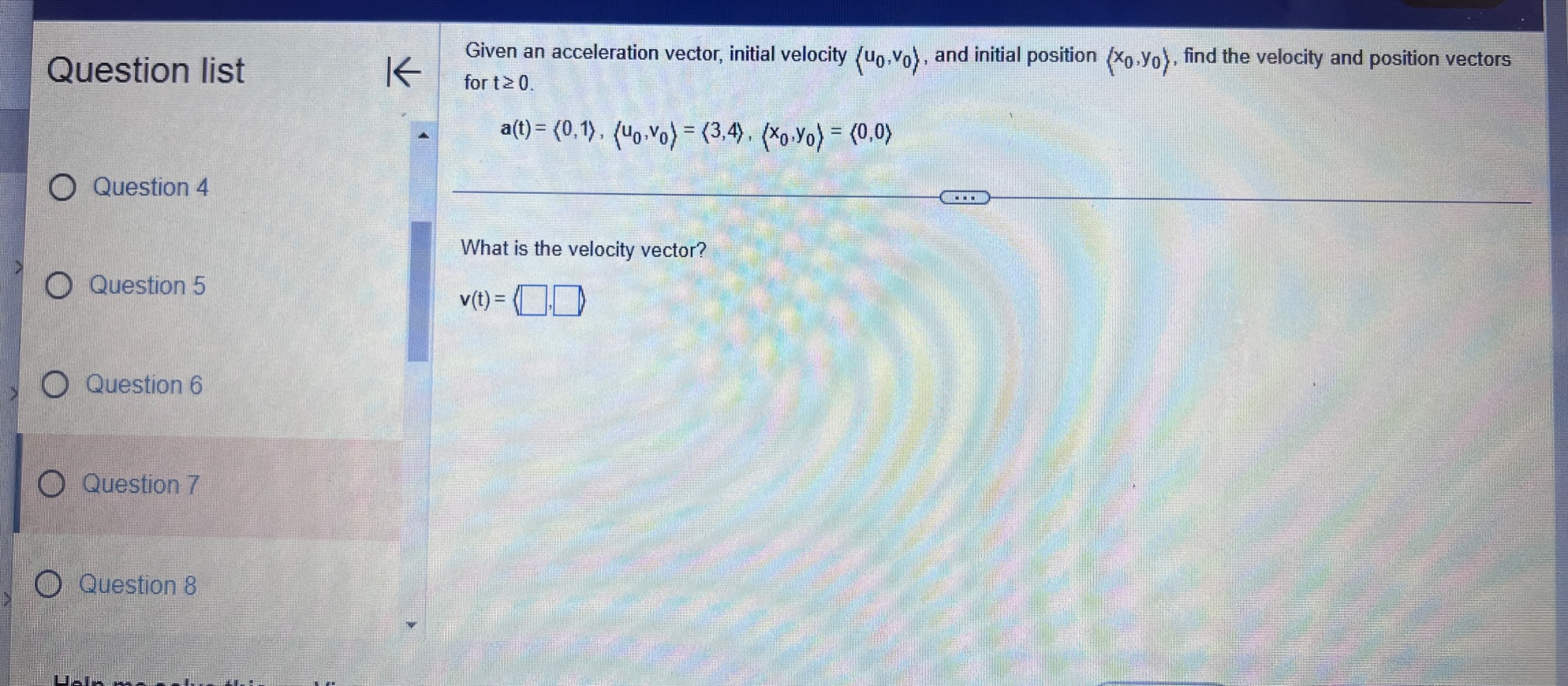
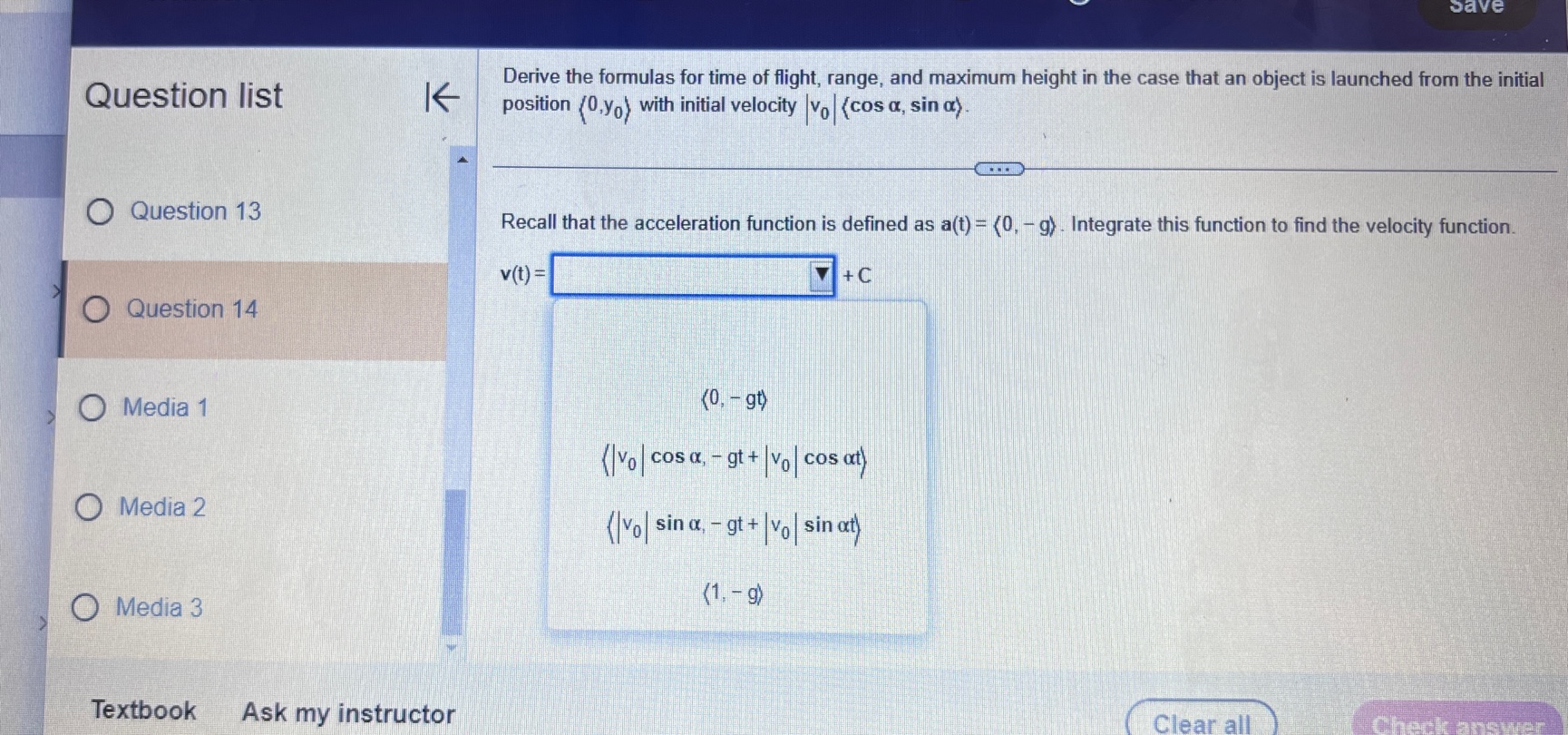
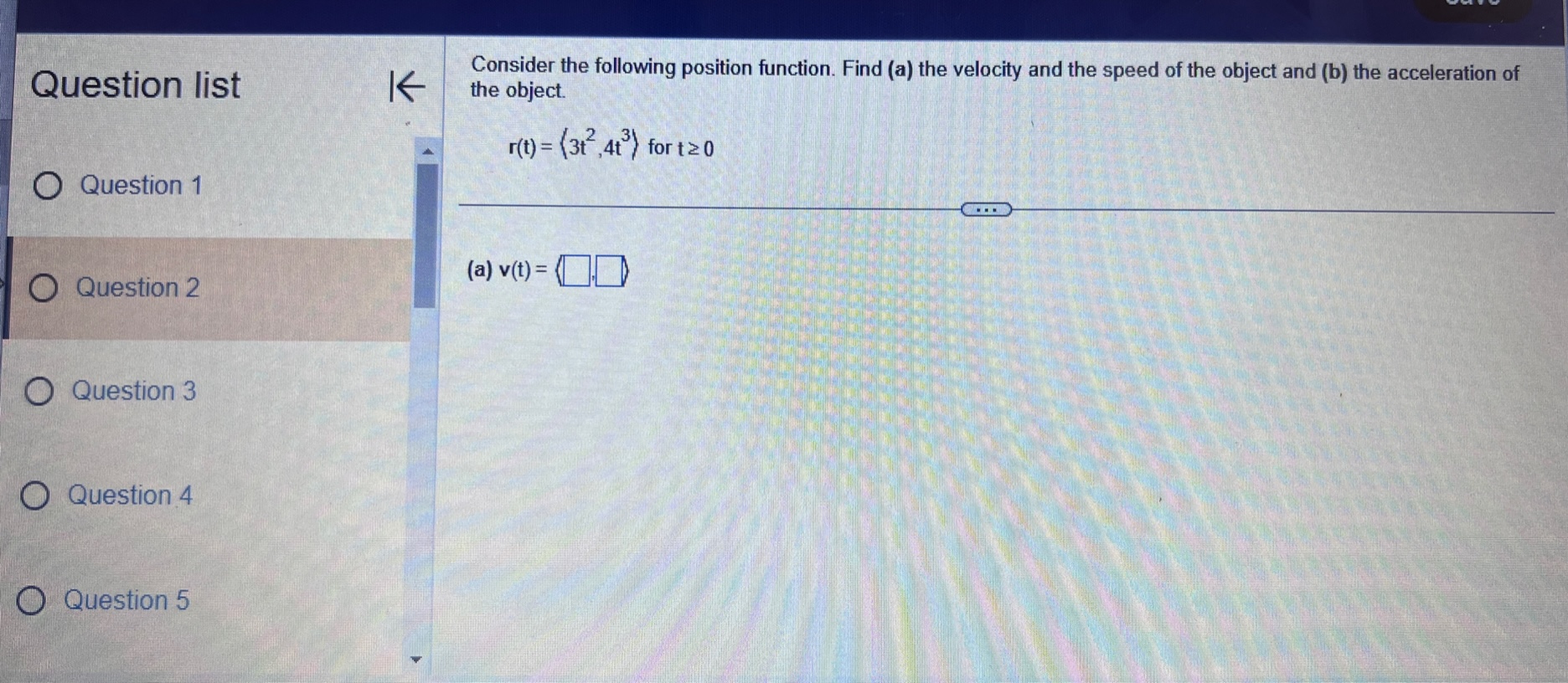
Question list A small rocket is fired from a launch pad 10 m above the ground with an initial velocity (200,450,550) m/s. A cross K wind blowing to the north produces an acceleration of the rocket of 3.5 m / s . Assume the x-axis points east, the y-axis points north, the positive z-axis is vertical (opposite g), and the ground is horizontal. Answer parts a through d. O Question 9 a. Find the velocity and position vectors for t 2 0. Question 10 The velocity vector is v(t) =( Question 11 Question 12 Question 13Question list K Consider the following position function. Find (a) the velocity and the speed of the object and (b) the acceleration of the object. r(1) = (312, 41 ) for t2 0 Question 1 Question 2 (a) v(t) = Question 3 Question 4 Question 5Consider the following position functions r and R for two objects. Question list K a. Find the interval [c,d] over which the R trajectory is the same as the r trajectory over [a, b]. b. Find the velocity of both objects. c. Graph the speed of the two objects over the intervals [a,b] and [c,d] respectively. For graphing, let c = 1 and d = 20. O Question 3 r(t) = (8 +12,2- 3t#,6 + 3t ), [a,b] =[0,6] R(t) = (8 + Int,2 - 3 In 2t,6 + 3 In 2t), on [c,d] Question 4 Question 5 a. The interval is (Simplify your answers.) Question 6 Question 7Given the position function r of a moving object, explain how to find the velocity, speed, and acceleration of the Question list K object. Question 1 Choose the correct answer below. O A. To find the velocity, integrate the position function. To find the speed, add the squares of each component of Question 2 the velocity function and take the square root. To find the acceleration, differentiate the position function. O B. To find the velocity, differentiate the position function. To find the speed, add the squares of each component of the velocity function and take the square root. To find the acceleration, differentiate the velocity function. Question 3 O C. To find the velocity, integrate the position function. To find the speed, add the squares of each component of the position function and take the square root. To find the acceleration, integrate the velocity function. O D. To find the velocity, differentiate the position function. To find the speed, add the squares of each component Question 4 of the acceleration function and take the square root. To find the acceleration, integrate the position function. Question 5K Consider the following position function. Find (a) the velocity and the speed of the object and (b) the acceleration of Question list the object. r(t) = (4 sin t,4 cost) for 0 sts 2n Question 1 (a) v(t) = O Question 2 Question 3 Question 4 Question 5Question list K Given an acceleration vector, initial velocity (Up.Vo,Wo), and initial position (X,Yozo), find the velocity and position vectors for t 2 0. a(t) = (7t, e -1,1), (up.vo, Wo) = (0,0,2). (xo.yoZo) = (6,0,0) Question 8 What is the velocity vector? Question 9 v(t) = ( Question 10 Question 11 Question 12 Video Textbook Ask my instructorQuestion list A projectile is fired over horizontal ground from the origin with an initial speed of 60 m/s. What firing angles will K produce a range of 350 m? Question y Angles of degrees will produce of range of 350 m. Question 10 (Do not round until the final answer. Then round to two decimal places as needed. Use a comma to separate answers as needed.) Question 11 Question 12 O Question 13 Question 14Ho ework: Section 14.3 Question 13, 14.3.67 Homework A golfer stands 420 ft (140 yd) horizontally ' Question "St '6 ' from the hole and 55 it above the hole (see > ' gure.)Assuming the ball is hit with an initial 55 U uuvsuull IU ' velocity of 120 his, at what angle (or angles) ' should it be hit to land in the hole? Assume the path of the ball lies in a plane. 420 (140 yd) 0 Question 11 E) The ball should be hit at an angle (or angles) of degrees. (Type an integer or decimal rounded to two decimal places as needed. Use a comma to separate answers as needed ) 0 Question 12 Save Question list K Determine whether the following trajectory lies on either a circle in R- or a sphere in R centered at the origin. If so, find the radius of the circle or sphere, and show that the position vector and the velocity vector are everywhere orthogonal. r(t) = (5 cos 2t,5 sin 2t), for 0 sts It Question 4 Question 5 Determine whether the following trajectory lies on either a circle in R- or a sphere in R centered at the origin. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. Question 6 O A. The trajectory lies on a sphere with radius . (Simplify your answer.) O B. The trajectory lies on a circle with radius . (Simplify your answer.) Question 7 O C. The trajectory does not lie on a circle or a sphere. Question 8Given an acceleration vector, initial velocity (up.Vo) , and initial position (*0,yo) . find the velocity and position vectors Question list K for t2 0. a(t) = (cost,3 sin t) , (uo.Vo) - (0.1) . (xo.yo) -(4,0) Question 6 O Question 7 What is the velocity vector? v(t) = 0 Question 8 Question 9 Question 10Question list K A projectile is launched at an angle of 450 to the horizontal from 6 it above the ground at an initial speed of 100 fu/sec. Assume the x-axis is horizontal, the positive y-axis is vertical (opposite g), the ground is horizontal, and only the gravitational force acts on the object. Answer parts a through d. Question 6 a. Find the velocity and position vectors for t2 0. Question 7 The velocity vector is v(t) =] Question 8 Question 9 Question 10 Video Textbook Ask my instructor Clear all Check answerQuestion list K Given an acceleration vector, initial velocity (Up.Vo) , and initial position (x,yo), find the velocity and position vectors for t2 0. a(t) = (0,1), (uo.Vo) = (3,4) , (xo.yo) = (0,0) Question 4 What is the velocity vector? Question 5 v (t) = 0 Question 6 Question 7 Question 8save Question list K Derive the formulas for time of flight, range, and maximum height in the case that an object is launched from the initial position (0.yo) with initial velocity vo (cos a, sin a) Question 13 Recall that the acceleration function is defined as a(t) = (0. -g) . Integrate this function to find the velocity function. v (t) = + C Question 14 O Media 1 (0, - gt) (|vo | cosa, - gt+ |vo|cos at) O Media 2 (|vol sin a, - gt + vo|sin at) O Media 3 (1, - g) Textbook Ask my instructor Clear all Check answerQuestion list K Consider the following position function. Find (a) the velocity and the speed of the object and (b) the acceleration of the object. r(1) = (3,ts , e - 1 ), for tz 0 Question 1 Question 2 (a) v(t) = Question 3 Question 4 Question 5
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


