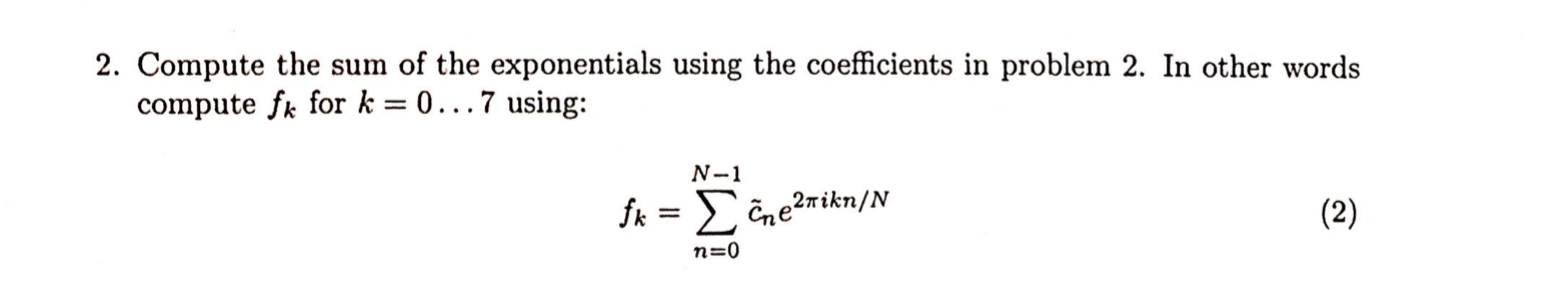Question number 2 is needed to be solved, but it based on question 1. Please solve the question in python Jupyter notebook.

1. Compute the coefficients of the discrete analogue of the fourier series when N = 8 for the sawtooth function, ie f(x) = x on the interval (0, 1) and periodic of period P= 1. In other words compute Cn for n = 0...7. N1 in = o E je zakon! (1) 2. Compute the sum of the exponentials using the coefficients in problem 2. In other words compute fk for k = 0... 7 using: V- 1 sx = lepe triany w ne2nikn/N 1 n =0 1. Compute the coefficients of the discrete analogue of the fourier series when N = 8 for the sawtooth function, ie f(x) = x on the interval (0, 1) and periodic of period P= 1. In other words compute Cn for n = 0...7. N1 in = o E je zakon! (1) 2. Compute the sum of the exponentials using the coefficients in problem 2. In other words compute fk for k = 0... 7 using: V- 1 sx = lepe triany w ne2nikn/N 1 n =0