Question:

Please help keep getting it wrong!

According to the WHO MONICA Project the mean blood pressure for people in China is 128 mmHg with a standard deviation of 23 mmHg. Assume that blood pressure is normally distributed.

Round the probabilities to four decimal places.

b) Find the probability that a randomly selected person in China has a blood pressure of 110.9 mmHg or more.

c) Find the probability that a randomly selected person in China has a blood pressure of 152.3 mmHg or less.

d) Find the probability that a randomly selected person in China has a blood pressure between 110.9 and 152.3 mmHg.

e) Find the probability that randomly selected person in China has a blood pressure that is at most 70.5 mmHg.

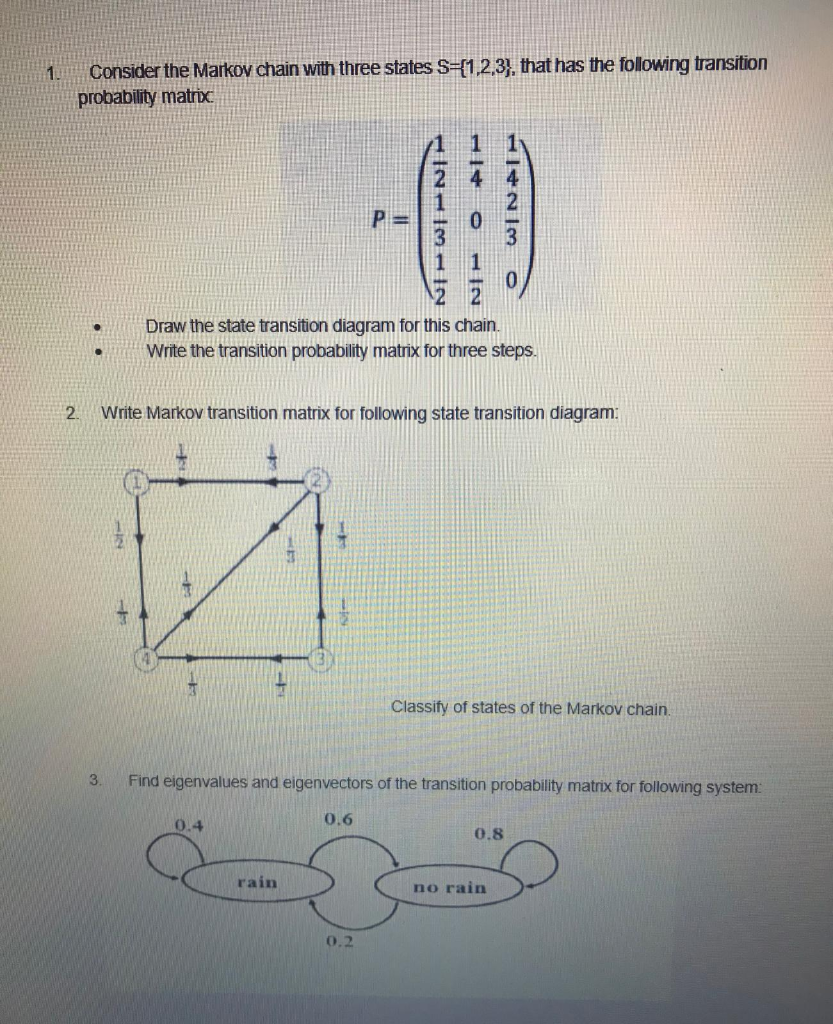
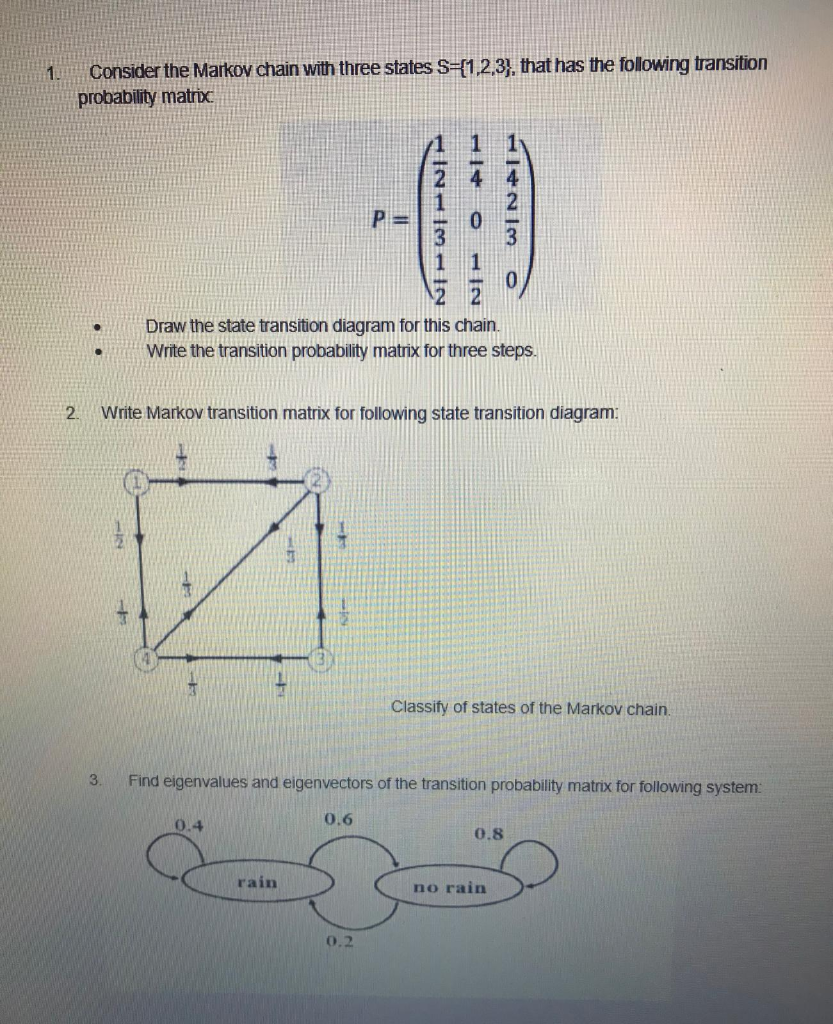
(1 mark each) For each of the given matrices, select all decompositions that can be applied to it. You do not have to show your work for this question. 2 ) A = [61 O Diagonalization (i.e., A = PDP-1 with D diagonal) O Schur triangularization O Spectral decomposition O Singular value decomposition b ) B = 0 1.001 Diagonalization O Schur triangularization O Spectral decomposition Singular value decomposition c) C is the 75 x 75 matrix with every entry equal to 1. Diagonalization Schur triangularization O Spectral decomposition Singular value decomposition d) D = 0 1 1 Diagonalization OSchur triangularization Spectral decomposition Singular value decompositionE. A Markov chain with the states 1, 2, 3 has transition probability matrix: 1 2 3 1 0.3 a 0.7 P = 2 0.4 0.3 b 3 c 0.2 [3.7 [3.] Give the values of o, b, and c that make the above a valid transition probability matrix. {3 points) (b) The 2-step transition probability matrix is 0.16 0.14 0.70 P12}: 0.2? 0.15 0.53 0.13 0.20 0.62 If the initial distribution of states is P0 = (0.3, [L7, [I], calculate the distribution of the states after 2 transitions. (3 points) (c) Will this Markov chain have a steady state distribution? Justify your mlswer. (2 points) 4. Consider the Markov chain X" = {X,} with state space S = {0, 1, 2, ...} and transition probabilities 1 ifj=i-1 Puj = 10 otherwise , for i 2 1 and Poo = 0, Poj = for j > 1. (a) Is this Markov chain irreducible? Determine the period for every state. (b) Is the Markov chain recurrent or transient? Explain. (c) Is the Markov chain positive recurrent? If so, compute the sta- tionary probability distribution. (d) For each state i, what is the expected number of steps to return to state i if the Markov chain X starts at state i? 5. Consider a Markov chain X = {X} with state space S = {0, 1, 2, ...} and transition probability matrix 0 1 0 0 P 0 0 P = O p 0 q 0 0 . . . 0 0 P 0 4 0 Here p > 0, q > 0 and p+q =1. Determine when the chain is positive recurrent and compute its stationary distribution.1. Consider the Markov chain with three states S=[1,2,3), that has the following transition probability matric 0 NI-WIHNI O Draw the state transition diagram for this chain. Write the transition probability matrix for three steps. 2. Write Markov transition matrix for following state transition diagram: Classify of states of the Markov chain. 3. Find eigenvalues and eigenvectors of the transition probability matrix for following system: 0.4 0.6 0.8 rain no rain