QUESTION TWO

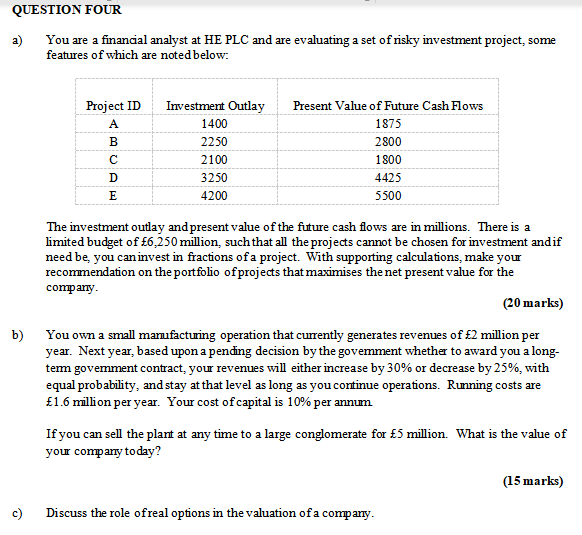
QUESTION ONE a) Consider an investor whose preferences are represented by the following utility function u(x) -In (2x), for x>0, where x denotes wealth, which is a realization of a random variable X (0). Derive the coefficients of absolute risk aversion, A(w) and of relative risk aversion R(w) for this agent. (10 marks) b) Consider an investor whose preferences are represented by the following utility function u(x) - -e*, for x>0, where x denotes wealth, whichis a realization of a random variabl X (0). Derive the change in the coefficients of absolute risk aversion and of relative risk aversion for this investor, as the investor's wealth changes. (10 marks) c) Discuss the merits ofnegative semi-variance as a measure ofrisk. (7 marks) d) Distinguish between risk and uncertainty (S marks) e) Discuss the use ofutility functions by financial firms in practice (15 marks) Suppose that there are V assets whose retums are jointly normally distributed. Frontier portfolios A and B are characterised below: Portfolio Expected Retums Standard Deviation 0.22 0.15 0.35 0.25 The variance ofa portfolio is given by w,2.42 + 2.w-( 1-w)..cB-pAB + (1-w)2-582 a) If PAB =-04, by how much do the retums of the minimum variance portfolio vary with the retums on portfolio A? (12 marks) b) Is portfolio C with an expected retum of0.29, an eficient portfolio? Explain. (8 marks) c) Compute the market premium, if the tangent portfolio, T has an expected retum of0.27 and when pAB 0.5. In solving this problem the product rule will be useful: For f(x) g(x) h(x):f(x) -gx)x)+g(x) h'(x) (15 marks) d) Explain the link between the Capital Market Line (CML) fromportfolio theory and the Securities Market Line (SML) that describes the Capital Asset Pricing Model (CAPM). (15 marks) QUESTION THREE a) If the correlation between two risky assets A and B is positive, can the variance of a portfolio that comprises A and B be zero, when shortpositions can be taken? Explain. (15 marks) b) If the correlation between two risky assets A and B is zero, can the variance of a portfolic that comprises A and B be zero, when short positions can be taken? Explain. (15 marks) c) Suppose you are going on a skiing holiday and are considering buying insurance. Your assessment ofthe likelihood ofincidents that need insuring is 5%. Such incidents cause a loss of 500 to your belongings and if there is no such incident, the loss is 0. Assume that you are an expected utility maximiser with a utility function)In x where x is the (this reflects the insurance premium and payment if you monetary value of your belongings purchase the travel insurance). You plan to take belongings worth 3000 on your trip Suppose there is only one insurance policy available. The policy pays you back the loss (i.e 500) in full, and its premium is 25. Should you buy this policy? Explain. (20 marks) QUESTION FOUR a) You are a financial analyst at HE PLC and are evaluating a set ofrisky investment project, some features of which are noted below: Project IDInvestment ay resent Value of Future Cash Flows 1400 1875 2800 2250 2100 1800 4425 3250 4200 5500 The investment outlay andpresent value of the future cash flows are in millions. There is a limited budget of 6,250 million, such that all the projects cannot be chosen for investment andif need be, you caninvest in fractions ofa project. With supporting calculations, make your reconmmendation on the portfolio ofprojects that maximises the net present value for the comparny (20 marks) b) year. Next year, based upon a pendng decision by the govemment whether to award you along term government contract, your revenues will either increase by 30% or decrease by 25%, with equal probability, and stay at that level as long as you continue operations. Running costs are 1.6 million per year. Your cost ofcapital is 10% per annum You own a small operation that currently generates revenues of 2 million per If you can sell the plant at any time to a large conglomerate for 5 million. What is the value of your company today? (15 marks) c) Discuss the role ofreal options in the valuation ofa company QUESTION ONE a) Consider an investor whose preferences are represented by the following utility function u(x) -In (2x), for x>0, where x denotes wealth, which is a realization of a random variable X (0). Derive the coefficients of absolute risk aversion, A(w) and of relative risk aversion R(w) for this agent. (10 marks) b) Consider an investor whose preferences are represented by the following utility function u(x) - -e*, for x>0, where x denotes wealth, whichis a realization of a random variabl X (0). Derive the change in the coefficients of absolute risk aversion and of relative risk aversion for this investor, as the investor's wealth changes. (10 marks) c) Discuss the merits ofnegative semi-variance as a measure ofrisk. (7 marks) d) Distinguish between risk and uncertainty (S marks) e) Discuss the use ofutility functions by financial firms in practice (15 marks) Suppose that there are V assets whose retums are jointly normally distributed. Frontier portfolios A and B are characterised below: Portfolio Expected Retums Standard Deviation 0.22 0.15 0.35 0.25 The variance ofa portfolio is given by w,2.42 + 2.w-( 1-w)..cB-pAB + (1-w)2-582 a) If PAB =-04, by how much do the retums of the minimum variance portfolio vary with the retums on portfolio A? (12 marks) b) Is portfolio C with an expected retum of0.29, an eficient portfolio? Explain. (8 marks) c) Compute the market premium, if the tangent portfolio, T has an expected retum of0.27 and when pAB 0.5. In solving this problem the product rule will be useful: For f(x) g(x) h(x):f(x) -gx)x)+g(x) h'(x) (15 marks) d) Explain the link between the Capital Market Line (CML) fromportfolio theory and the Securities Market Line (SML) that describes the Capital Asset Pricing Model (CAPM). (15 marks) QUESTION THREE a) If the correlation between two risky assets A and B is positive, can the variance of a portfolio that comprises A and B be zero, when shortpositions can be taken? Explain. (15 marks) b) If the correlation between two risky assets A and B is zero, can the variance of a portfolic that comprises A and B be zero, when short positions can be taken? Explain. (15 marks) c) Suppose you are going on a skiing holiday and are considering buying insurance. Your assessment ofthe likelihood ofincidents that need insuring is 5%. Such incidents cause a loss of 500 to your belongings and if there is no such incident, the loss is 0. Assume that you are an expected utility maximiser with a utility function)In x where x is the (this reflects the insurance premium and payment if you monetary value of your belongings purchase the travel insurance). You plan to take belongings worth 3000 on your trip Suppose there is only one insurance policy available. The policy pays you back the loss (i.e 500) in full, and its premium is 25. Should you buy this policy? Explain. (20 marks) QUESTION FOUR a) You are a financial analyst at HE PLC and are evaluating a set ofrisky investment project, some features of which are noted below: Project IDInvestment ay resent Value of Future Cash Flows 1400 1875 2800 2250 2100 1800 4425 3250 4200 5500 The investment outlay andpresent value of the future cash flows are in millions. There is a limited budget of 6,250 million, such that all the projects cannot be chosen for investment andif need be, you caninvest in fractions ofa project. With supporting calculations, make your reconmmendation on the portfolio ofprojects that maximises the net present value for the comparny (20 marks) b) year. Next year, based upon a pendng decision by the govemment whether to award you along term government contract, your revenues will either increase by 30% or decrease by 25%, with equal probability, and stay at that level as long as you continue operations. Running costs are 1.6 million per year. Your cost ofcapital is 10% per annum You own a small operation that currently generates revenues of 2 million per If you can sell the plant at any time to a large conglomerate for 5 million. What is the value of your company today? (15 marks) c) Discuss the role ofreal options in the valuation ofa company