Question(B) need to be solved by Python.

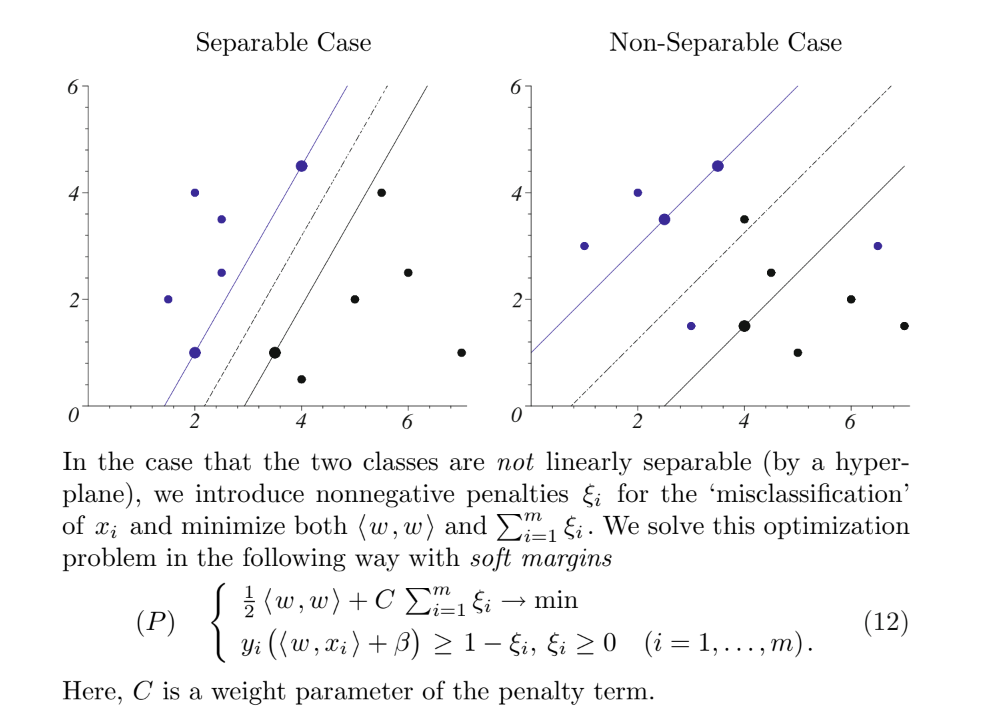
Support Vector Machines (cf. [Cr/Sh) Support vector machines have been extensively used in machine learning and data mining applications such as classification and regression, text categorization as well as medical applications, for example breast cancer diagnosis. Let two classes of patterns be given, i. e., samples of observable characteristics which are represented by points xi in R". The patterns are given in the form (xi,yi), i- 1,..., m, with yi E {1,-11. y means that xi belongs to class 1; otherwise xi belongs to class 2. In the simplest case we are looking for a separating hyperplane described by (w,x)+B-0 with w,m) + 1 if yi-1 and w, ay + --1 if yi =-1. These conditions can be written as i (w,xi ) 2 1 (i -1,..., m). We aim to maximize the 'margin' (distance) 2/V/(w, w) between the two hyperplanes w,2) + -1 and w,z) + =-1. This gives a linearly constrained convex quadratic minimization problem Support Vector Machines (cf. [Cr/Sh) Support vector machines have been extensively used in machine learning and data mining applications such as classification and regression, text categorization as well as medical applications, for example breast cancer diagnosis. Let two classes of patterns be given, i. e., samples of observable characteristics which are represented by points xi in R". The patterns are given in the form (xi,yi), i- 1,..., m, with yi E {1,-11. y means that xi belongs to class 1; otherwise xi belongs to class 2. In the simplest case we are looking for a separating hyperplane described by (w,x)+B-0 with w,m) + 1 if yi-1 and w, ay + --1 if yi =-1. These conditions can be written as i (w,xi ) 2 1 (i -1,..., m). We aim to maximize the 'margin' (distance) 2/V/(w, w) between the two hyperplanes w,2) + -1 and w,z) + =-1. This gives a linearly constrained convex quadratic minimization