questions

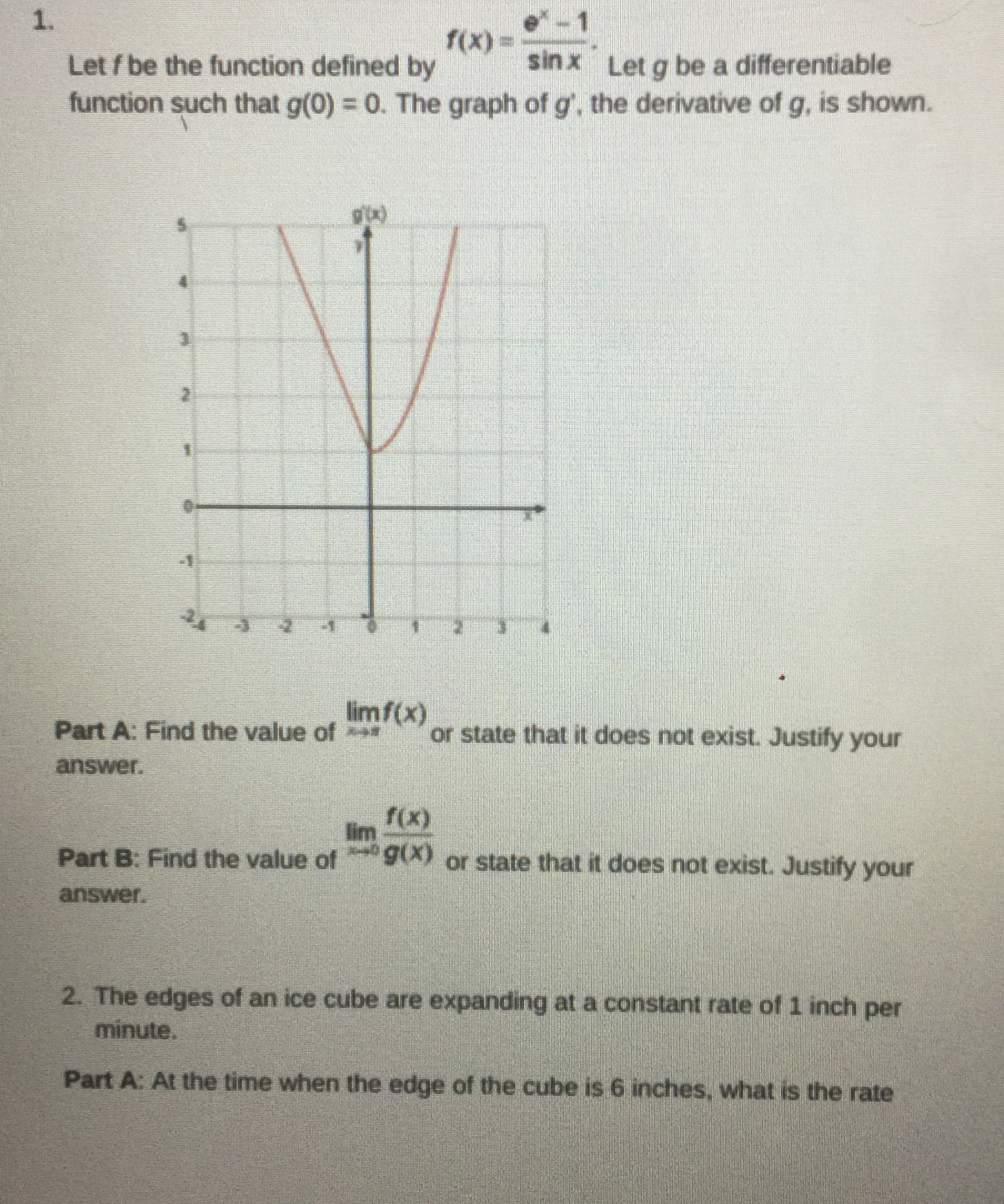
1. Let / be the function defined by f(x) = sin x Let g be a differentiable function such that g(0) = 0. The graph of g', the derivative of g, is shown. Part A: Find the value of lim f(x) or state that it does not exist. Justify your answer. f(X) Part B: Find the value of "g(X) or state that it does not exist. Justify your answer. 2. The edges of an ice cube are expanding at a constant rate of 1 inch per minute. Part A: At the time when the edge of the cube is 6 inches, what is the rateof increase of its volume? Part B: How fast is the surface area of the cube changing when each edge of the cube is 8 inches? dV -25. Part C: A second ice cube is changing such that of Interpret the meaning of this value and describe how the second ice cube is changing. 3. A cylindrical container filled with snow cone syrup has a diameter of 4 inches and a height of 10 inches. The container is full of syrup and leaking at a rate of 2 in /hr. The syrup is leaking into an empty conical snow cone cup with a diameter of 2.5 inches and a height of 3.5 inches. Part A: How fast is the depth of the syrup changing when the level in the cylindrical container is 8 inches high? Part B: At what time will the cylindrical syrup container be empty? Part C: At what rate is the depth of the syrup in the conical cup rising when the syrup in the cup is 1 inch deep? Indicate units of measure. 4. A particle moves along the x-axis so that its position, in feet, at time ( seconds is given by y(() = 412 + 6t + 2 - e' for time O s t s 5. Part A: What is the velocity of the particle when the acceleration is zero? Part B: When is the particle moving to the right? Justify your answer. Part C: At time t = 2, is the particle speeding up or slowing down? Give a reason for your answer.5. Let f be a differentiable function. Selected values of f and its derivative f are given in the table in the closed interval -2 s x s 2, where f ' is strictly increasing on the interval (0, 2) X -2 -1 N ((x ) 10 7 S 7 10 f'(x) -1 -2 -2 -1 Part A: Find the linearization ((x) at the point where x = 1. Part B: Use the line from part A to approximate the value of f(1.3). Is this approximation greater than or less than the actual value of /(1.3)? Give a reason for your