Questions A thru E

a. What is the probability that all three orders will be filled correctly?

b. What is the probability that none of the three orders will be filled correctly?

c. What is the probability that at least two of the three orders will be filled correctly?

d. What are the mean and standard deviation of the binomial distribution used in (a) through (c)? Interpret these values.

The mean is

The standard deviation is

On average, ( ) orders are correctly filled, while there is an approximate variation of ( ) from the (average /minimum / maximum) number of orders (taken / correctly filled / incorrectly filled)

e. Compare the results of (a) through (d) with those of the two restaurants given in the popup tables.(Restaurant B / Restaurant C / The restaurant you and your friends attended / It cannot be determined which restaurant) has a slightly higher probability of filling orders correctly.

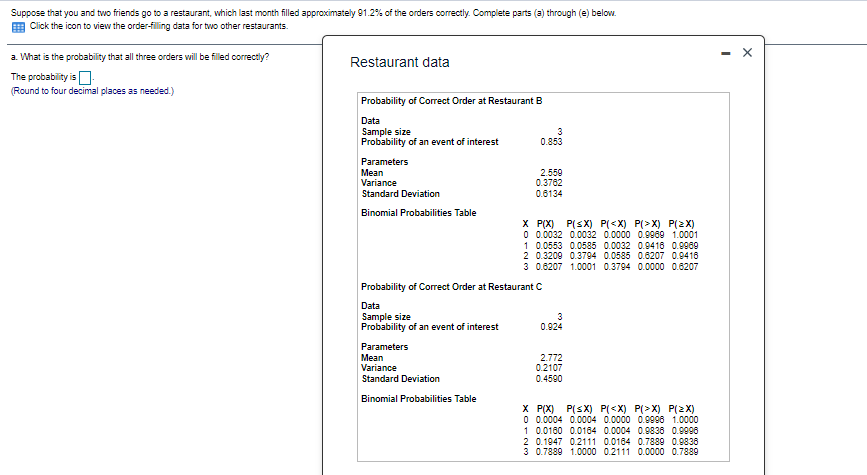
Suppose that you and two friends go to a restaurant, which last month filled approximately 91.2% of the orders correctly. Complete parts (a) through (e) below. Click the icon to view the order-filling data for two other restaurants. a. What is the probability that all three orders will be filled correctly? X Restaurant data The probability is]. (Round to four decimal places as needed.) Probability of Correct Order at Restaurant B Data Sample size 3 Probability of an event of interest 0.853 Parameters Mean 2.559 Variance 0.3782 Standard Deviation 0.6134 Binomial Probabilities Table X P(X) P(EX) P(X) P(2X) 0 0.0032 0.0032 0.0000 0.8989 1.0001 1 0.0553 0.0585 0.0032 0.9416 0.0989 0.3209 0.3794 0.0585 0.6207 0.0416 3 0.8207 1.0001 0.3794 0.0000 0.8207 Probability of Correct Order at Restaurant C Data Sample size 3 Probability of an event of interest 0.924 Parameters Mean 2.772 Variance 0.2107 Standard Deviation 0.4590 Binomial Probabilities Table X P(X) P(EX) P(X) P(2X) 0 0.0004 0.0004 0.0000 0.8996 1.0000 0.0180 0.0184 0.0004 0.9836 0.0996 0.1947 0.2111 0.0184 0.7889 0.9836 0.7889 1.0000 0.2111 0.0000 0.7889