questions below:

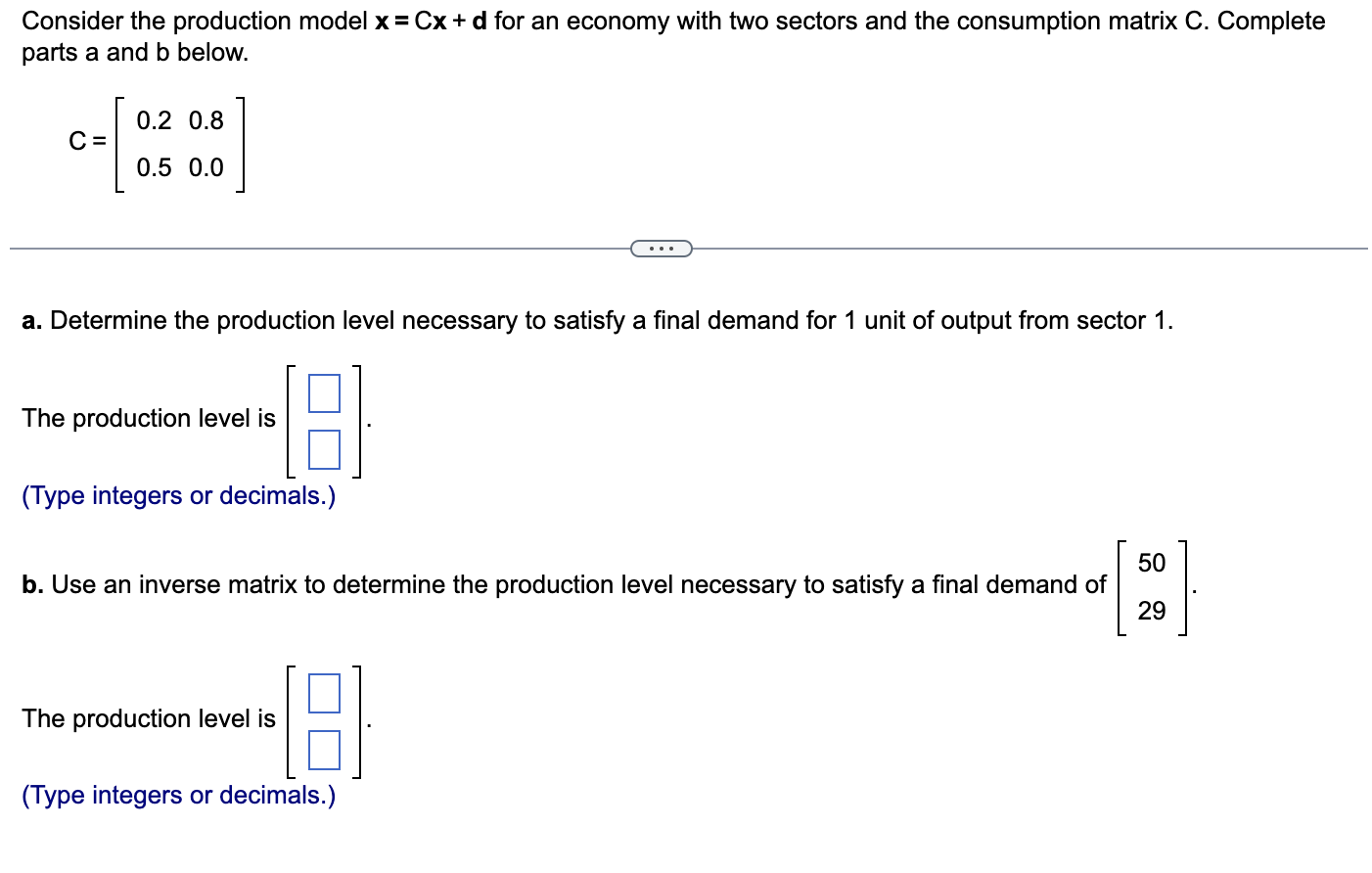
Consider the production model x = Cx + d for an economy with two sectors and the consumption matrix C. Complete parts a and b below. 0.2 0.8 C= 0.5 0.0 . . . a. Determine the production level necessary to satisfy a final demand for 1 unit of output from sector 1. The production level is (Type integers or decimals.) 50 b. Use an inverse matrix to determine the production level necessary to satisfy a final demand of 29 The production level is (Type integers or decimals.)\fDetermine the values of the parameter s for which the system has a unique solution, and describe the solution. 5sx, + 7X2 = 3 8x1 + 4sX2 = - 3 . . . Choose the correct answer below. 3( - 5s - 8) 3(4s + 7) OA. SFO; X1 = ;X = (552 -14) 1(5s2 - 14) 14 3(4s + 7) 3( - 5s - 8) OB. SF ; X2 = 4 (5s2- 14) 4 (5s2 - 14) 3(4s + 7) 3( - 5s - 8) OC. S* 0; X 1 : X2 4 5s - 14) 4 5s - 14) 14 3( - 5s - 8) 3(4s + 7) OD. SF+ 5 ;X2 = 4 (5s2 - 14) 4 5s2- 14)Find formulas for X, Y, and Z in terms of A, B, and C. It may be necessary to make assumptions about the size of a matrix in order to produce a formula. [Hint: Compute the product on the left, and set it equal to the right side.] Find the formulas for X, Y, and Z. Note that I represents the identity matrix and 0 represents the zero matrix. X = Y = Z=