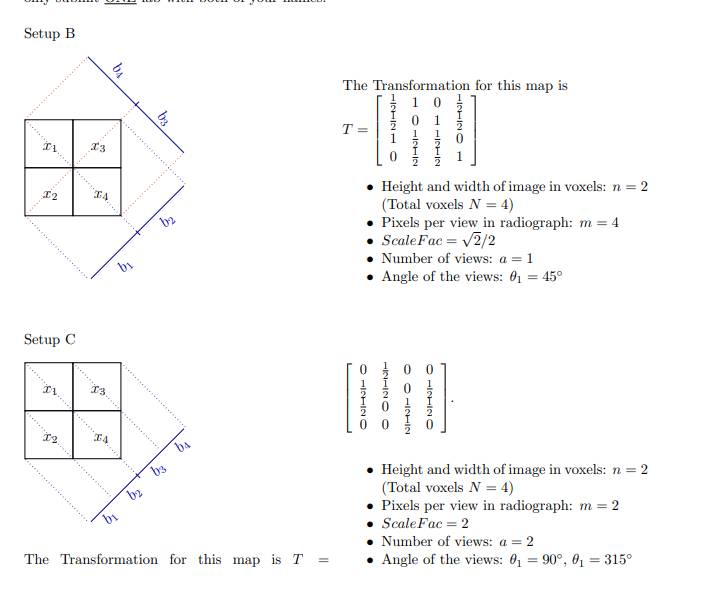
Questions for Each Setup Answer the following questions for Set Up B and Setup C. First answer questions for Set up B then answer all questions for Setup C (to help with grading). Then answer the general questions below. Thanks! 1. Describe the set of all invisible objects by finding a basis for this space. Are any nonzero objects invisible to this operator? If so, give an example. (See your Pre-Lab for the definitions: nonzero object and invisible object.) 2. Is it possible for two different objects to produce the same radiograph? If so, give an example and subtract them. What is special about the resulting object? 3. Describe the set of radiographs that can be produced from all possible objects. 4. Are there radiographs (in the appropriate dimension for the problem) that cannot be pro- duced as the radiograph of any object? If so, give an example. 5. Find a basis for the space of all possible radiographs. That is, find a linearly independent set of radiographs that spans the space of possible radiographs. 6. Do you think this transformation is injective? Why or why not? 7. Do you think this transformation is onto? Why or why not? Question: In this lab, you found bases for two different vector spaces (invisible objects, and possible radiographs). What reasons might you be interested in these bases, in the context of radiography? Setup B Setup C b t b 4. b3 b2 ba ba b b b3 The Transformation for this map is T = The Transformation for this map is T = HINHINO HOLICHIN OHHICHIN HINHINOL 10 Height and width of image in voxels: n = 2 (Total voxels N = 4) Pixels per view in radiograph: m = 4 Scale Fac= 2/2 Number of views: a = 1 Angle of the views: 0 = 45 OHINHINO HINHINO O HIGHIN HINHIN O Height and width of image in voxels: n = 2 (Total voxels N = 4) Pixels per view in radiograph: m = 2 Scale Fac = 2 Number of views: a = 2 Angle of the views: 0 = 90, 0 = 315