Questions:

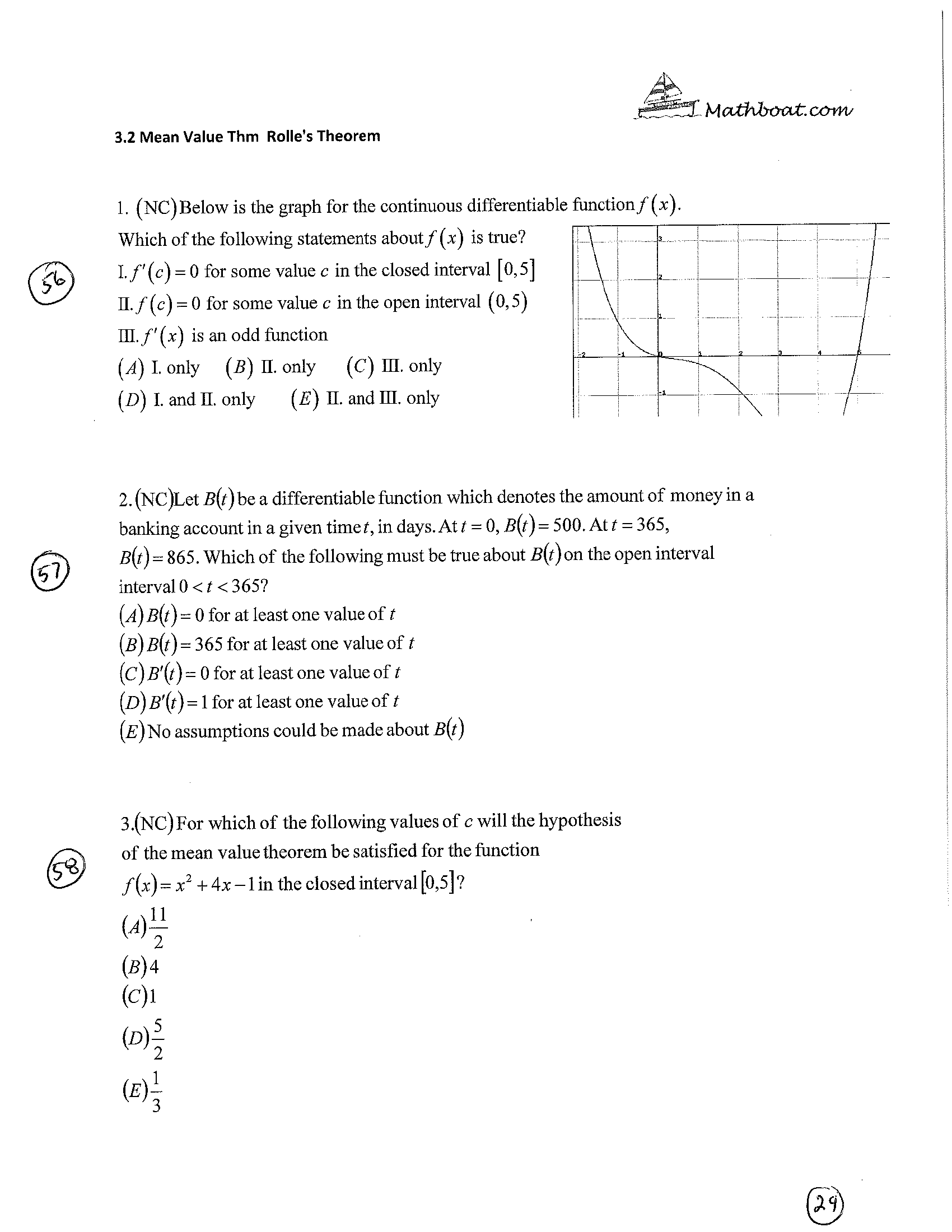
J.Mathboat.com 2.6a Implicit Differentiation 1(NC). What is the slope of the tangent line to the curve (x' + y)' - 2a xy = b' at the point P(0, 1) when a = V2 and b = 1? 36 (A) -2 (B) -2 ( C) 2 (D) 1 ( E) 2 2. (NC) Which of the following is y' if xy + sec y = 8? (A) -2xy . (x2 sec y tan y) (B xy sec y tan y sec y tan y 37 (C) -2 -2xy (D)- x - sec y tan x -2xy (E) - x' + sec y tan y 3NC. For what values of x does the curve y' - x* + 2xy -18x2 =10 have vertical tangent lines? ( A) x - 5 (B) x = -2y (C) x = -y (D) x = 5, x = -5 (E) x=2y SKIP 20@ 7 (C) For What values ofx does the curvey 2.25x2 3.25x = 2 have horizontal tangent lines? 8 (N C). The rate at which the function y = cos2 x is increasing at x 2% is k times the rate at which x is increasing. What is the value of k ? (A)? (BrJ25 (0); (Di-1 (E)1 @ 2.7 Related Rates 1(NC). A circle is inscribed in a square. The circumference of the circle is increasing at a constant rate of 6 in/sec. As the circle expands, the square expands to keep the circle inscribed. At what rate is- the perimeter of the square increasing? (A) Ein/sec (B) Ein/sec (C) 24 in/sec (D) gin/sec (E) 36 in/sec 7: 7t 7t 2. (C) Water runs into a conical tank at the rate of 3 ft3 / min. The tank stands pointing down and has a height of 15 ft and a base radius of 4 ft. How fast is the water level rising when the water is 8 ft deep? (A)0.210ft/min (3)0.021 / min (0)0.070 ft/ min (D)0.220ft/rnin (E)0.041ft / min 3NC A circle is inscribed in a square. The area of the circle is increasing at a constant rate of 1571 in2 /sec. As the circle expands, the square expands to keep the circle inscribed. At what rate is the area of the square increasing in in2 /sec? (A)30 (B) 120 (C) 6: (D) % (E) 60 @ 4NC) A 25 meter ladder leans against a wall. It starts sliding from 15 meters above the ground. The foot of the ladder is pulled away from the wall at the rate of 6 In / sec.What is the rate (in m/sec) at which top of the ladder is sliding down? ) )- ('30:: E (A ( ( l (D) 11 ( ) SNC. Sand leaks at 36 cubic meters/ sec into a cone shaped pile that has a radius always equai to the height. When the radius is 3 meters, at what rate (in m/sec) is the height changing? Mathboat.com 6NC. Two bikers start at the same place and same time. The first biker rides east at a constant velocity of 5 miles per hour and the second biker rides north at a constant velocity of 12 miles per hour. Approximately how fast (in mph) is the distance between them changing after 3 hours? 48 ( A) 5 B 7 (C) 12 (D) 13 (E) 17 INC. How fast (in m/sec) does the water level rise when a cylindrical container with radius 17 meters is filled at the rate of 5m/sec? 5 ( A) 289T (B) 289 (0) 2 289n 5 (D) 5x E) 289 25Mathbout.com 3.1 Extrema of functions INC. Which of the following are the absolute extrema of the function f(x) = 3x2 -9x + 8 on the interval [-2,3] ? 50 (A) max 8, min (B) max 38, min 8 (C) max 38, min Alu (D) max 9, min 0 (E) max 9, min -21 2NC. If f (x) = x' - 6x, which of the following are the maximum 51 and minimum on the interval [-3,2]? (4) Max:f ( V2) , Min: f (-V2) (B) Max:f (V2) ,Minif (-3) (C) Max:f (-V2) ,Min:f (2) (D) Max:f (-V2), Min:f (-3) 3C. What are the critical points of the function f defined by: 52 f ( x) = (7x+ 2)2 5x3+1 ? A) -0.2857,-0.5848 (D)-0.5297,-0.5848 (B) -0.2857, -0.5297 (E) -0.2857, -0.5297, -0.5848 (C)-0.5848 261 4C. What are the critical points for the equation y = 3((4x)2 + 2x +1)3 ? (A) -0.0556 (B) 00625 (C) 0.0625 (D) -0.0625, -0.0556 (E) 00625, -0.0556 5C. How many local minima and maxima does the graph y : sin2 x + cos(3x) + 3x have in the interval [1, 3] ? (A) l min only (B) 1 max only (C) l min 1 max (D) 1 min 2 max (E) none s" 6NC. How many different critical numbers does the function f(x) = (x+2)3 (2x 5) 2 have? (A) none (B) one (C) two (D) three (E) four 3.2 Mean Value Thm Rolle's Theorem 1. (NC) Below is the graph for the continuous differentiable function f (x) Which of the following statements about f (x) is true? L l. f'(c) = 0 for some value c in the closed interval [0,5] 11. f (c) = 0 for some value c in the open interval (0, 5) D1.f'(x) is an odd function (A) I. only (B) H. only (C) 111. only (D) I. and II. only (E) H. and 1]]. only 2. (NC)Let B(t) be a differentiable function which denotes the amount of money in a banking account in a given time t, in days. At t = 0, 3(2) = 500. At t = 365, B(t) = 865. Which of the following must be true about B(t) on the open interval interval 0