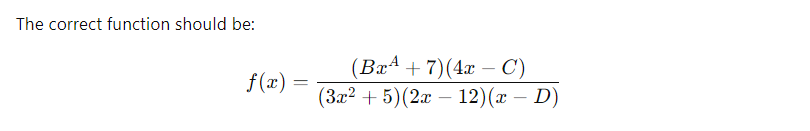
QUIZ 2 MATH 115 Instructions: UM ID: 2908 9928 . Total points = 20 points Initials: RH . Note that there are 25 points on this quiz. The quiz will be graded out of 20 points, so if you score higher than 20 points, you may receive extra credit. Show your work for all answers. . You should submit your solutions on Canvas by 11:59 pm on Wednesday, September 18th. Problems: 1. (5 points) Each year lake Erie reaches its minimum temperature of 32 degrees Fahrenheit ( F) on March 1st and its maximum temperature of 760 F on September 1st. Write a formula for a sinusoidal function T(m) modeling the lake's temperature, in F, m months after January 1st. 2. (7 points) Consider the rational function f (20) = 7 (BaA + 7) (4x - C) (32 2 + 5) (22 - 12) (2 - D) where A, B, C, and D are constants. Suppose that . y = 12 is a horizontal asymptote of f(x) . x = 7 is the only vertical asymptote of f(x). Find the values of A, B, C, and D. 3. (3 points) Find a formula for one polynomial p(x) that satisfies both of the following properties: . The degree of p(x) is at least 5, but no greater than 8; . The domain of the function In(p(x)) is the interval (-co, co). Note that this problem may have more than one correct answer. You only need to find one correct answer.4. (10 points) While planning for a quiz, Jen wants to predict how much time it would take her to grade all 23 of her students' quizzes. She knows from previous experience that when she grades, she starts slow and grades faster along the way. Suppose that Jen starts grading at 7:00 P.M., and suppose g(m) represents the number of quizzes that Jen has graded m minutes after 7:00 P.M. 9(m) = 10em/100 - 10 For the questions below give the exact answer and then use a calculator to give an ap- proximate numerical answer. (a) (6 points) For the following table fill in the question marks (?). You must show work to receive full credit. m 0 ? 100 In (15 ) ( 24 ) 6 ? 1 ? 23 Using your table from part (a), answer the questions below. i. (1 points) How long will it take Jen to grade the first quiz? ii. (1 points) How long will it take Jen to grade all of her student' quizzes? iii. (2 points) How long will it take her to grade the last quiz (That is, how long did it take her to grade only the 23rd quiz)?\fLet's solve Problem 2 again, correcting the mistake about A. Problem Setup We are given the rational function: (BaA + 7) (4x - C) f (x) = (3x2 + 5) (2x - 12) (x - D) with the conditions: 1. y = 12 is the horizontal asymptote. 2. x = 7 is the only vertical asymptote.Step 1: Horizontal Asymptote To find the horizontal asymptote, we compare the degrees of the numerator and denominator. * Numerator: The degree of the numeratoris A + 1 (since the term Bztis multiplied by 4, resulting in B4+, Denominator: The degree of the denominator is 4 (since multiplying 3z2 - 2z - = 6z*). For there to be a horizontal asymptote at y = 12, the degrees of the numerator and denominator must match. This gives the condition: A+1=4 = A=3 MNow, using the horizontal asymptote condition y = 12, we take the ratio of the leading coefficients: B-4 Z 12 6 Solving for B: Step 2: Vertical Asymptote Vertical asymptotes occur where the denominator is zero but not the numerator. We are told that x = T is the only vertical asymptote. Therefore, one factor of the denominator must be (z 7). Given the denominator is (322 + 5)(2z 12)(x D), for = = T to be a vertical asymptote, we set D =T. Final Function Substituting all values into the function, we get: (182 + 7)(4x O) @) = G ez - 2@ -7 where (' remains a general constant. \fLet's double-check the solution to Problem 2: 1. Horizontal asymptote: . The degree of the numerator is A + 1 and the denominator is degree 4. We found that A = 3 for the degrees to match. V . The horizontal asymptote y = 12 gives = 12, leading to B = 18. V 2. Vertical asymptote: = 7 as the vertical asymptote gives D = 7. 3. Unspecified constant: C remains unspecified, which is fine. V