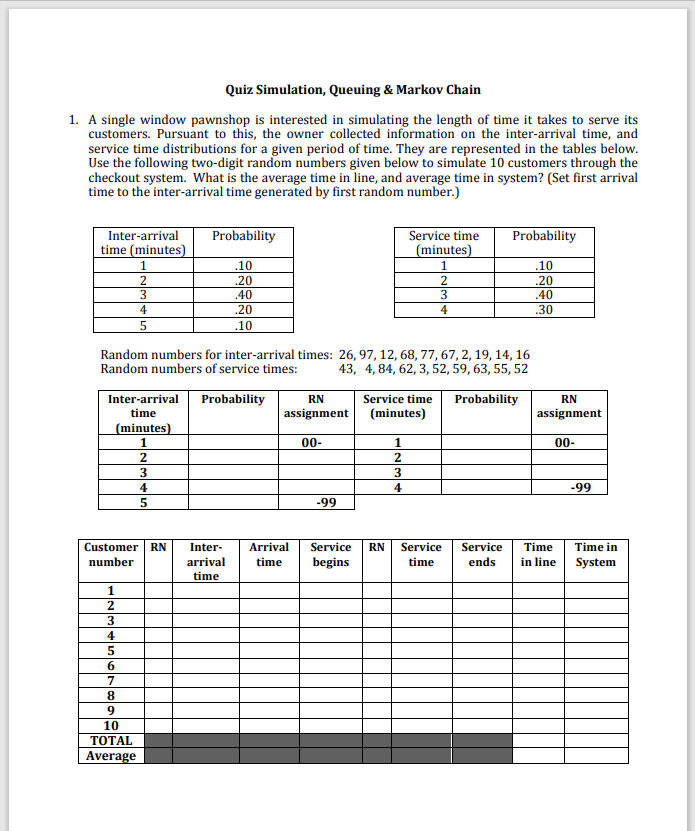
Quiz Simulation, Queuing & Markov Chain 1. A single window pawnshop is interested in simulating the length of time it takes to serve its customers. Pursuant to this, the owner collected information on the inter-arrival time, and service time distributions for a given period of time. They are represented in the tables below. Use the following two-digit random numbers given below to simulate 10 customers through the checkout system. What is the average time in line, and average time in system? (Set first arrival time to the inter-arrival time generated by first random number.) Inter-arrival Probability Probability time (minutes) 1 2 3 4 10 .20 Service time (minutes) 1 2 3 4 .10 .20 .40 .20 .40 .30 5 .10 Random numbers for inter-arrival times: 26, 97, 12, 68,77,67, 2, 19, 14, 16 Random numbers of service times: 43, 4, 84, 62, 3, 52, 59, 63,55,52 Inter-arrival Probability RN Service time Probability RN time assignment (minutes) assignment 00- 00- (minutes) 1 2 3 4 5 1 2 3 4 -99 -99 Arrival Service RN Service Time Time in Customer RN number Inter- arrival time Service ends time begins time in line System 1 2 3 4 5 6 7 8 9 10 TOTAL Average