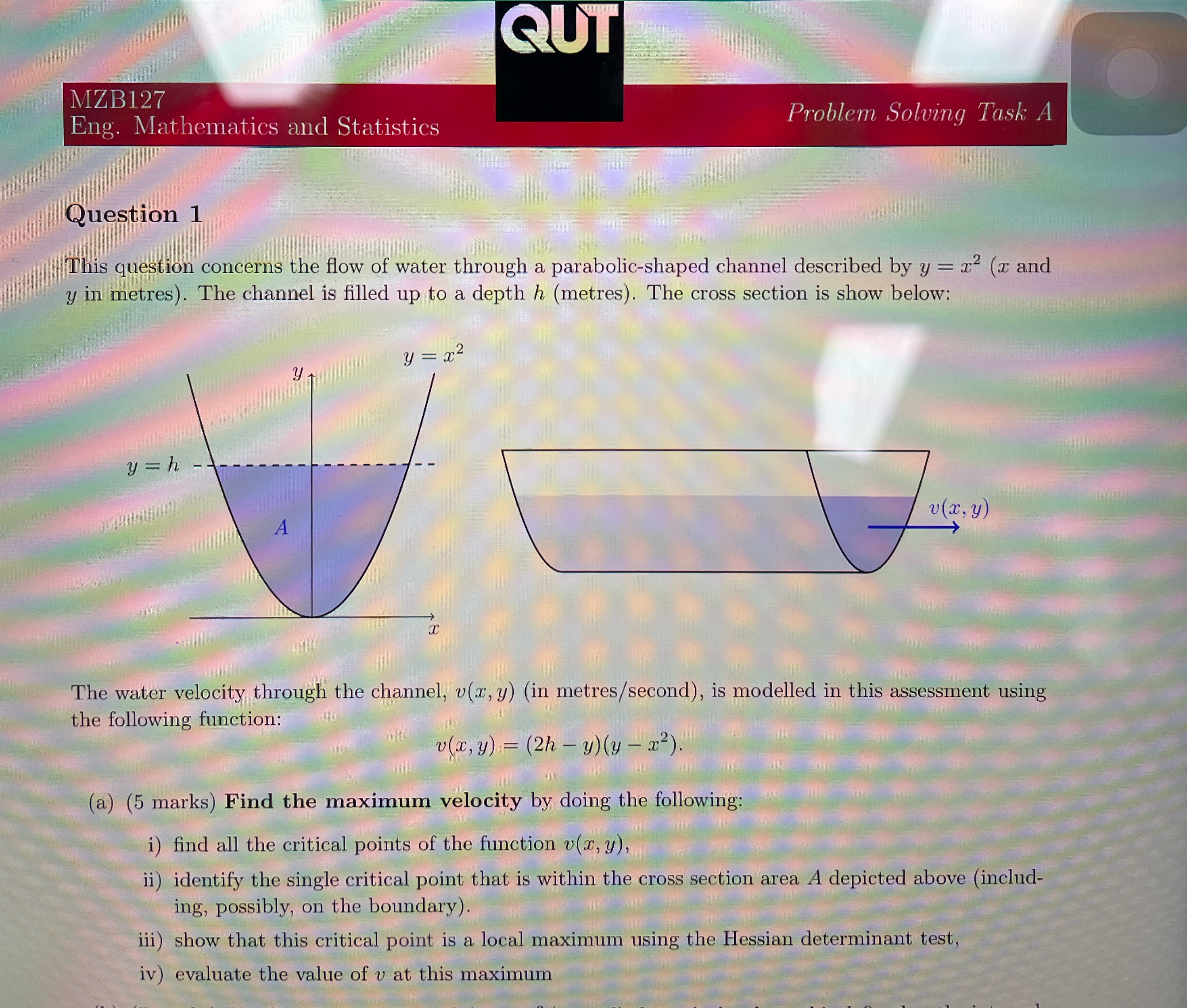
Question: QUT MZB127 Eng. Mathematics and Statistics Problem Solving Task A Question 1 This question concerns the flow of water through a parabolic-shaped channel described by
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


