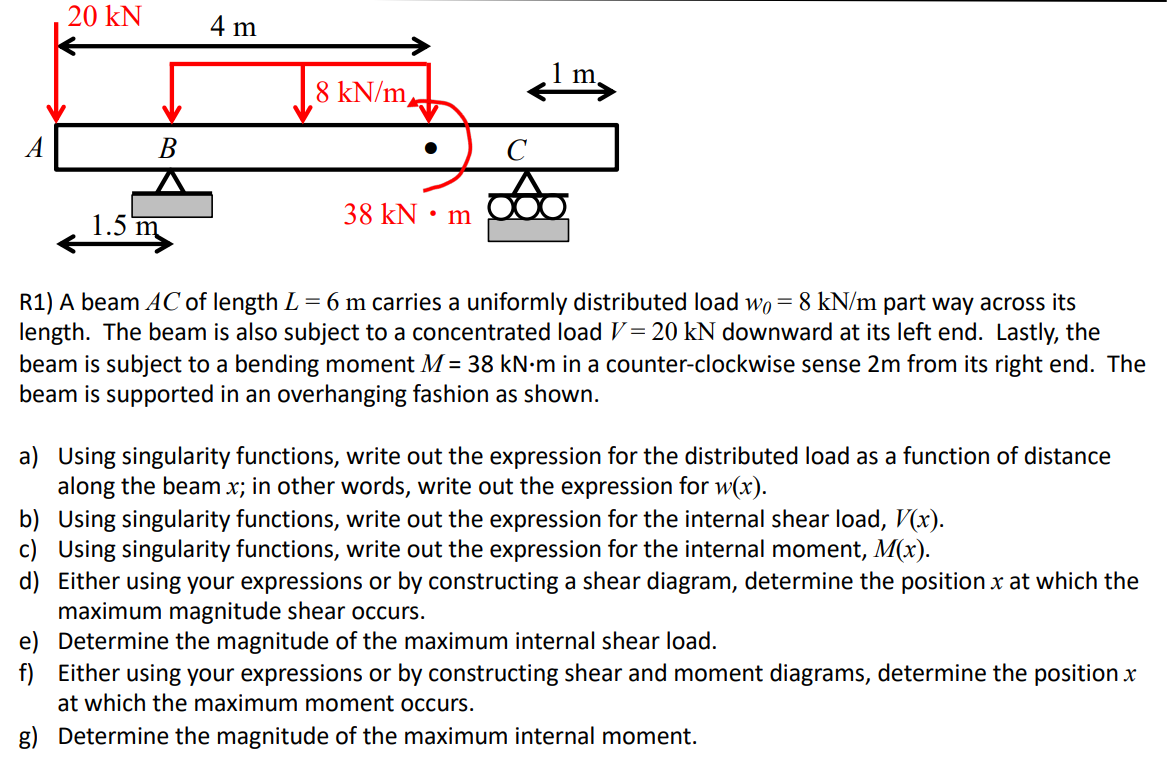
R$1)$ A beam $\backslash ($ A C $\backslash )$ of length $\backslash ($ L$=6\backslash$mathrm$\{$~m$\}\backslash )$ carries a uniformly distributed load $\backslash ($ w$\_\{0\}=8\backslash$mathrm$\{$kN$\}/\backslash$mathrm$\{$m$\}\backslash )$ part way across its length. The beam is also subject to a concentrated load $\backslash ($ V$=20\backslash$mathrm$\{$kN$\}\backslash )$ downward at its left end. Lastly, the beam is subject to a bending moment $\backslash ($ M$=38\backslash$mathrm$\{$kN$\}\backslash$cdot $\backslash$mathrm$\{$m$\}\backslash )$ in a counter$-$clockwise sense $2$ m from its right end. The beam is supported in an overhanging fashion as shown.

a$)$ Using singularity functions, write out the expression for the distributed load as a function of distance along the beam $\backslash ($ x $\backslash )$; in other words, write out the expression for $\backslash ($ w$($x$)\backslash ).$

b$)$ Using singularity functions, write out the expression for the internal shear load, $\backslash ($ V$($x$)\backslash ).$

c$)$ Using singularity functions, write out the expression for the internal moment, $\backslash ($ M$($x$)\backslash ).$

d$)$ Either using your expressions or by constructing a shear diagram, determine the position $\backslash ($ x $\backslash )$ at which the maximum magnitude shear occurs.

e$)$ Determine the magnitude of the maximum internal shear load.

f$)$ Either using your expressions or by constructing shear and moment diagrams, determine the position $\backslash ($ x $\backslash )$ at which the maximum moment occurs.

g$)$ Determine the magnitude of the maximum internal moment.