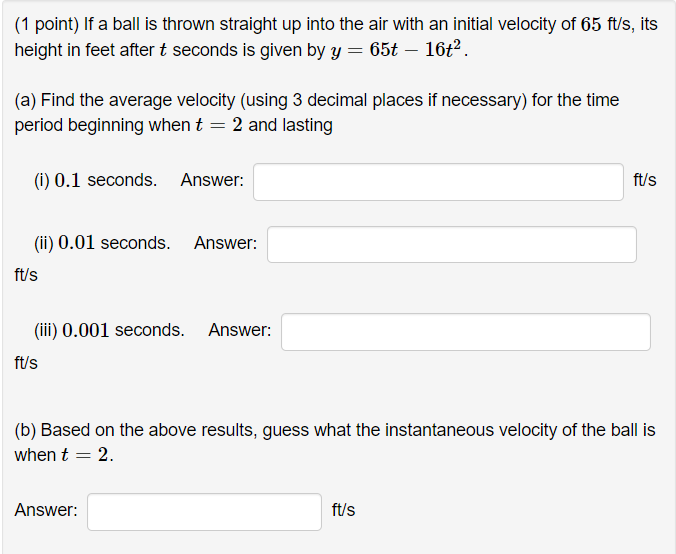
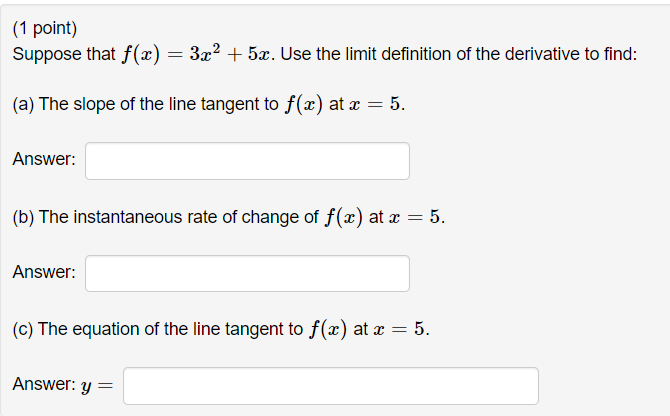
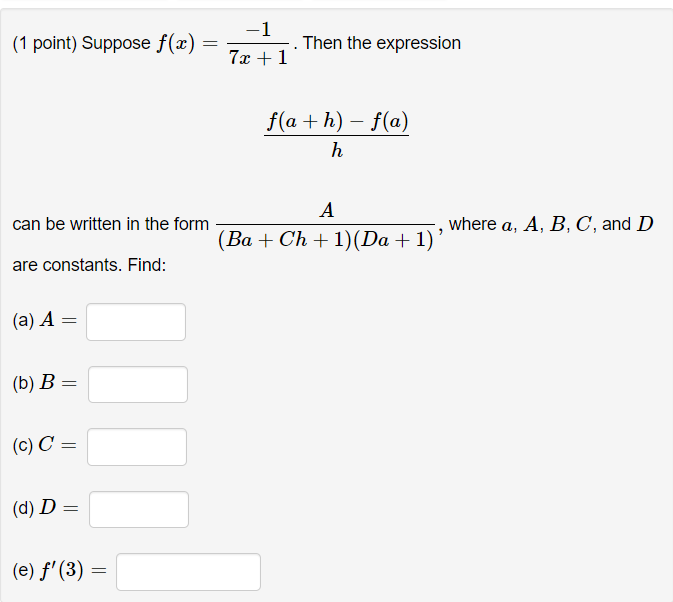
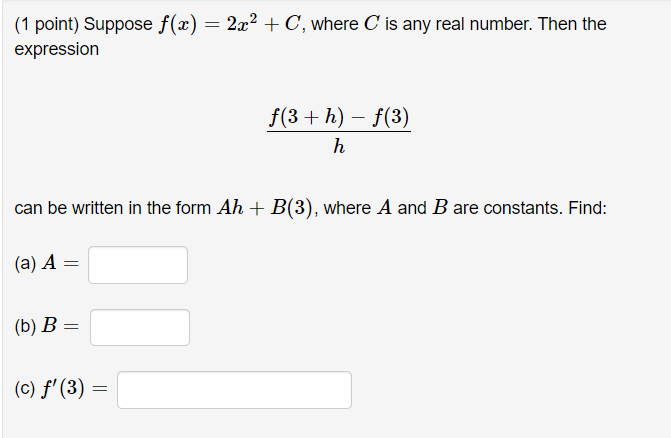
r- 6 (1 point) Use interval notation to indicate where f (a ) = is (2 - 1) (2 + 1) continuous. Answer: T E Note: Input U, infinity, and -infinity for union, oo, and -oo, respectively.(1 point) If a ball is thrown straight up into the air with an initial velocity of 65 ft/s, its height in feet after t seconds is given by y = 65t - 16t2. (a) Find the average velocity (using 3 decimal places if necessary) for the time period beginning when t = 2 and lasting (i) 0.1 seconds. Answer: ft/s (ii) 0.01 seconds. Answer: ft/s (iii) 0.001 seconds. Answer: ft/s (b) Based on the above results, guess what the instantaneous velocity of the ball is when t = 2. Answer: ft/s(1 point) Suppose that f(a) = 3x2 + 5x. Use the limit definition of the derivative to find: (a) The slope of the line tangent to f(x) at x = 5. Answer: (b) The instantaneous rate of change of f (a ) at a = 5. Answer: (c) The equation of the line tangent to f (x ) at x = 5. Answer: y =(1 point) Suppose f(a) = -8x2 + 2. Evaluate the following limit. lim f (4 + h) - f(4) h-0 h Note: Input DNE, infinity, -infinity for does not exist, oo, and -oo, respectively.(1 point] Suppose f($) = _1 .Then the expression 71: + 1 + h) ) h A can be written in the form where a, A, B, C, and D (Bo + Ch + 1)(Do + 1} ' are constants. Find: (3}A 2 (m3 = (cw = (d}D = {e} 1'13) = (1 point) Suppose f(a) = 2x2 + C, where C is any real number. Then the expression f (3 + h) - f(3) h can be written in the form Ah + B(3), where A and B are constants. Find: (a) A = (b) B = (c) f' (3) =