R programming

Subject:

Example 11.2.1

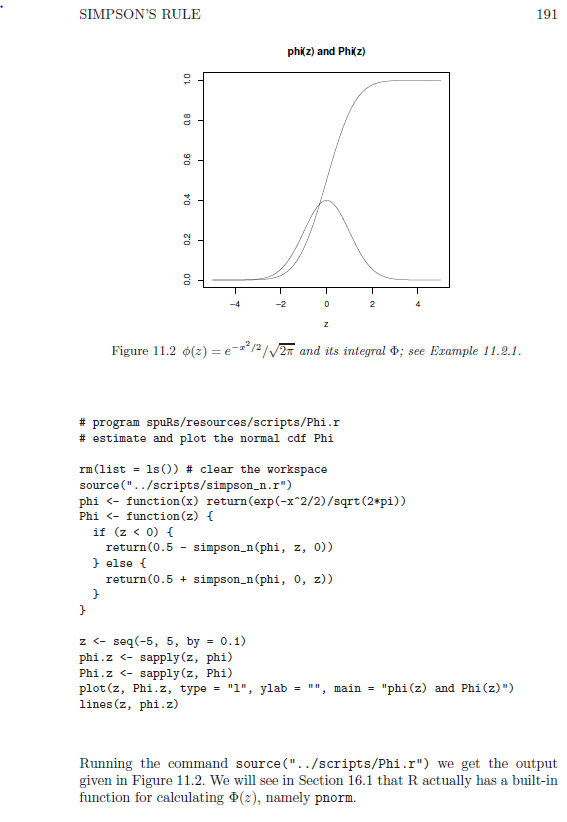
3. The standard normal distribution function is given by (z)=z21ex2/2dx. For p[0,1], the 100p standard normal percentage point is defined as that 200 NUMERICAL INTEGRATION zp for which (zp)=p. Using the function Phi (z) from Example 11.2.1, calculate zp for p=0.5, 0.95,0.975, and 0.99. Hint: express the problem as a root-finding problem. 11.2.1 Example: (z)Phi.r One of Gauss' many prodigious acts was to compile by hand tables of (z)= z21ex2/2dx, estimated to several decimal places. (This is the distribution function of a normal or Gaussian random variable; see Section 16.5.1.) Thankfully we can now do this using a computer, as follows. Figure 11.2(z)=ex2/2/2 and its integral ; see Example 11.2.1. \# program spuRs/resources/scripts/Phi.r \# estimate and plot the normal cdf Phi rm( list =1s()) \# clear the workspace source("../scripts/simpson_n.r") phi (exp(x2/2)/sqrt(2i)) Phi (z