Random Variable

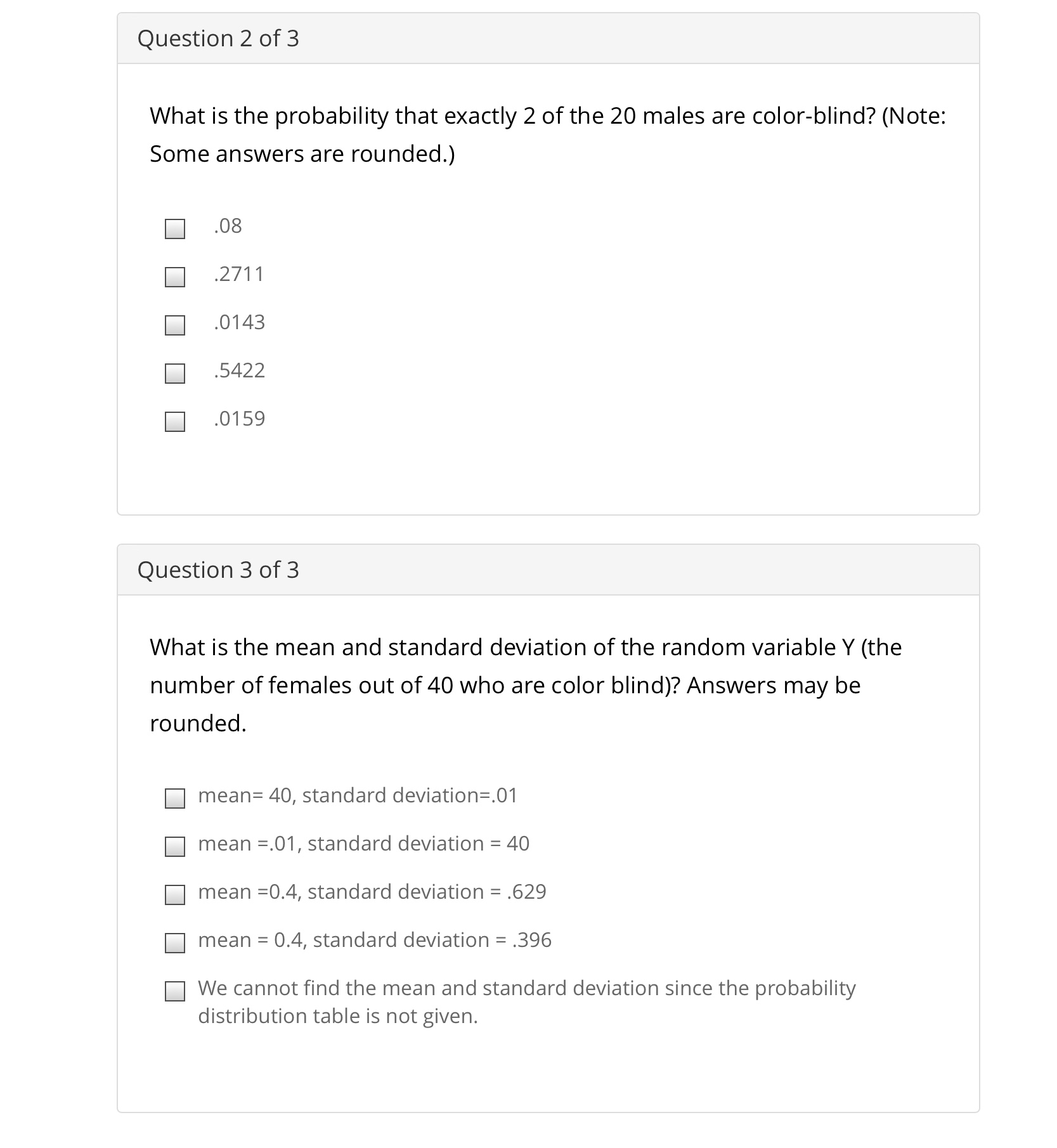
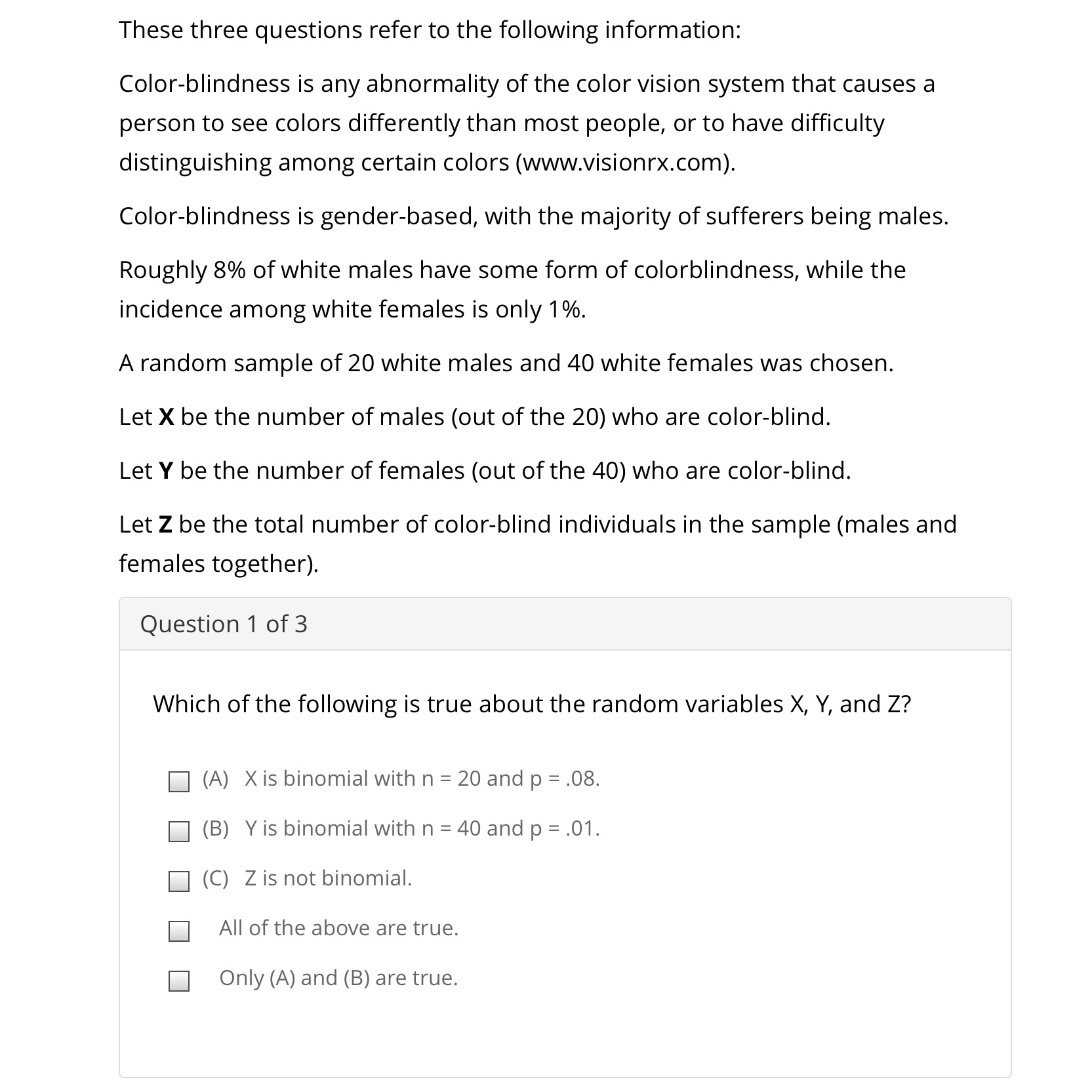
Question 2 of 3 What is the probability that exactly 2 of the 20 males are color-blind? (Note: Some answers are rounded.) .08 .2711 .0'l43 .5422 .0159 DEBBIE Question 3 of 3 What is the mean and standard deviation of the random variable Y (the number offemales out of40 who are color blind)? Answers may be rounded. |:| mean: 40, standard deviation=.01 |:| mean =.01, standard deviation = 40 D mean =O.4, standard deviation = .629 |:| mean = 0.4, standard deviation = .396 D We cannot find the mean and standard deviation since the probability distribution table is not given. These three questions refer to the following information: Color-blindness is any abnormality of the color vision system that causes a person to see colors differently than most people, or to have difficulty distinguishing among certain colors (www.visionrx.com). Color-blindness is gender-based, with the majority of sufferers being males. Roughly 8% ofwhite males have some form of colorblindness, while the incidence among white females is only 1%. A random sample of 20 white males and 40 white females was chosen. Let X be the number of males (out of the 20) who are color-blind. Let Y be the number of females (out ofthe 40) who are color-blind. Let 2 be the total number of color-blind individuals in the sample (males and females together). Question 1 of 3 Which ofthe following is true about the random variables X, Y, and Z? |:| (A) X is binomial with n = 20 and p = .08. D (B) Y is binomial with n = 40 and p = .01. |:| (C) Z is not binomial. |:| All of the above are true. |:| Only(A)and(B)aretrue