Question: Random variable $X$ and $y$ have joint PDF $$ f_{X, Y} (x, y)=left{begin{array}{11} 6 e^{-(2 x+3 y);, & x geq 0, y geq 0 .

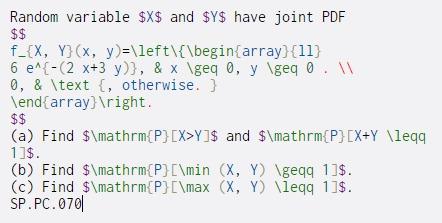
$Random variable $X$ and $y$ have joint PDF $$ f_{X, Y}$

Random variable $X$ and $y$ have joint PDF $$ f_{X, Y} (x, y)=\left\{\begin{array}{11} 6 e^{-(2 x+3 y);, & x \geq 0, y \geq 0 . \\ 0, & \text {, otherwise. } \end{array} ight. $$ (a) Find $\mathrm{P][X>Y]$ and $\mathrm{P][X+Y \leqq 1]$. (b) Find $\mathrm{P][\min (X, Y) \geqq 1]$. (c) Find $\mathrm{P] [\max (X, Y) \leqq 11$. SP.PC.0701

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Random variable $X$ and $y$ have joint PDF $$ f_{X, Y}(x, y)=\left\{\begin{array}{11} 6 e^{-(2 x+3y)}, & x \geq 0, y \geq 0.1 0, & \text {, otherwise. } \end{array} ight. $$ (a) Find...

I have three questions. About #117 and #118, I know how to solve like with 0 About #119, I got a, b, d, but I could not get the correct answers on c and e. Could you help me to solve them? The...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Prolog You are approached to compose a Prolog program to work with twofold trees. Your code shouldn't depend on any library predicates and you ought to expect that the mediator is running without...

Hi Erylee88, I would like to utilize your service again. Same format different questions. Please find attached document for your review. Let me know. Thank you, Sam...

Determine the hazard rate function for the random variable Exercise 8 (#1.22). Let v be a measure on a o-field F on ? and f and g be Borel functions with respect to F. Show that (i) if f fdy exists...

Review the t test scenarios the three different approaches of t tests: Independent sample t test Paired sample t test One sample t test Analysis of your t test results for each research scenario and...

This question is similiar to https://www.coursehero.com/tutors-problems/Management/27083519-Chairvana-Inc-manufactures-metal-tables-and-chairs-at-its-plant-in-Pa/ Lawnvana's Broadcast Spreader...

1. Describe a sample space in rolling two six-side fair dice. Define the events: A= (at least one "6" appears), B= (the sum of dots on the dice is divisible by 3). Find AUB, A0B, A-B, B-A, A', B',...

If most investors expect the same cash flows from Companies A and B but are more confident that A`s cash flows will be closer to their expected value, which company should have the higher stock...

Ponyfish Limited acquired 70% of the issued shares of Seahorse Limited for $23,000,000 on 1 January 2017. The shareholders' equity of Seahorse Limited on 1 January 2017 was as follows: Issued share...

A company borrowed $ 1 2 0 , 0 0 0 from a local bank. The loan requires 1 0 equal annual payments beginning one year from today. Assume an interest rate of 7 % . What is the amount of each annual...

Seved Help 14 Wisconsin Snowmobile Corp. is considering a switch to level production Cost efficiencies would occur under level production, and aftertax costs would decline by $31,500, but inventory...

Explain the difference between Job Analysis, Job Classification, and Job Evaluation.

What does Processing of an OLAP Cube accomplish?

After designing a Multidimensional Database in Visual Studio, what are the next steps that build the Database in the Analysis Services Instance? How is the build out of the Analytical Services...