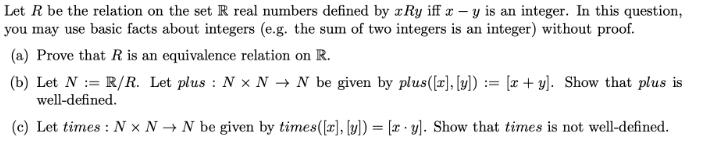
real numbers defined by aRy iff x - y is an integer. In this question, Let R be the relation on the set you may use basic facts about integers (e.g. the sum of two integers is an integer) without proof. (a) Prove that R is an equivalence relation on R. on (b) Let N := R/R. Let plus : N x N N be given by plus((r), [y]) := [x + y). Show that plus is well-defined. (c) Let times : N x N N be given by times(r), [y]) = [r y]. Show that times is not well-defined. %3!