Really need help with these questions! Any help would be much appreciated! Thank you so much!

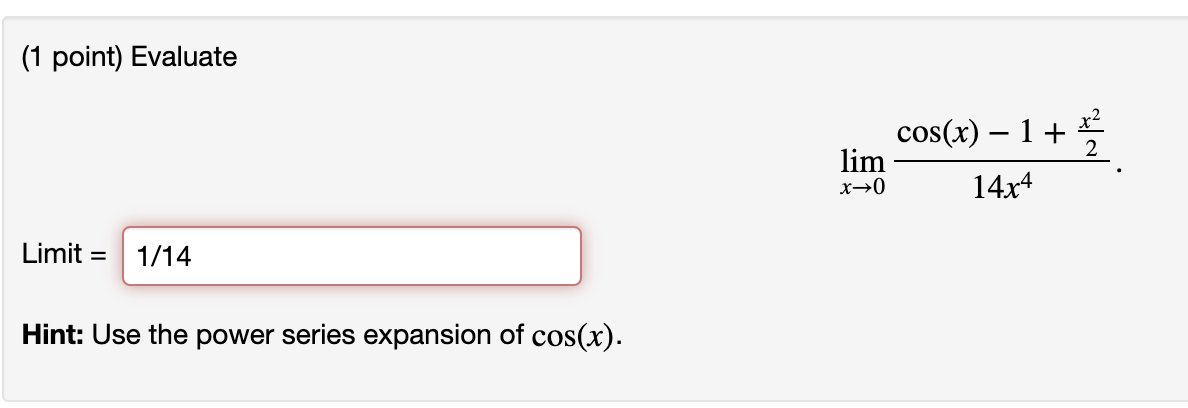
(1 point) Find the first five non-zero terms of Taylor series centered at x = 4 for the function below. f(x) = f Answer: f (x) = + + + + What is the radius of convergence? Answer: R = inf no (1 point) Represent the function 9111(7 x) as a power series (Maclaurin series) for) = 2 Cal\" n=0 Co: Find the radius of convergence R = . (1 point) f(x) = x sin(x) Compute m = _ m) = _ m = m = _ m = m = _ W) = m = _ fm= We): _ m = me) = _ We see that for the odd terms f (2k+1)(0) = and we also see that for the even derivatives f (mm) = for k z 1 except for k = 0. -1'\\(k-1)2k Hence the Taylor series for f centered at 0 is given by f(x) = z 2k/(2k!)*-1 A(k-1) ka. k=1 (1 point) Evaluate cos(x) 1 + % x>0 14364 Limit: 1/14 Hint: Use the power series expansion of cos(x)- 00 (1 point) The Taylor series for f(x) = x/ 10660 + x at a = 0 is 2 can Or)". n=0 Find the first few coefficients. co: c1= Find the error in approximating 10076 = f(76) using the third degree Taylor polynomial off at a = 0_ That is, find the error of the approximation v 10076 x T3 (76). (1 point) Suppose that Find the following coefficients. a: s 2 9 || || || || 9 || Find the radius of convergence R of the power series. 8x _ x+15 _ Zenx". n=0 7 . (1 point) Represent the function as a power senesf(x) = c x" (1 8x)2 2 " co = _ 02 = as = Find the radius of convergence R = . n=0