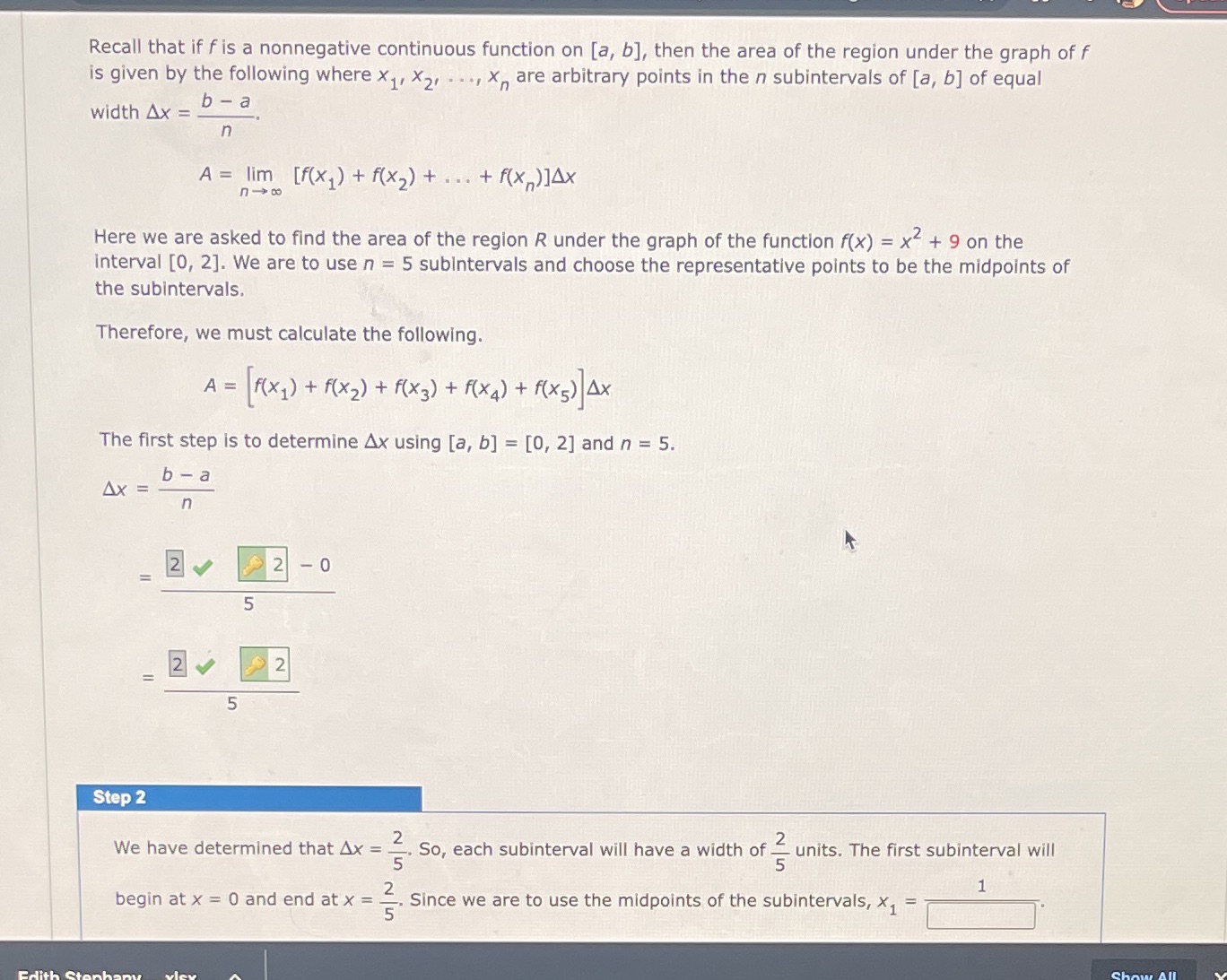
Recall that if f is a nonnegative continuous function on [a, b], then the area of the region under the graph of f is given by the following where X1, X2, ..., x, are arbitrary points in the n subintervals of [a, b] of equal width Ax =_ b - a n A = lim [f(x,) + f(x2) + ...+ f(x, )14x Here we are asked to find the area of the region R under the graph of the function f(x) = x + 9 on the interval [0, 2]. We are to use n = 5 subintervals and choose the representative points to be the midpoints of the subintervals. Therefore, we must calculate the following. A = f( x 1 ) + f ( x 2 ) + f ( x 3 ) + ( ( x 4 ) + ( ( x 5 ) Ax The first step is to determine Ax using [a, b] = [0, 2] and n = 5. AX = b - a n 2 0 2 0 12 0 2 5 Step 2 We have determined that Ax = . So, each subinterval will have a width of _ units. The first subinterval will 1 begin at x = 0 and end at x = 2 Since we are to use the midpoints of the subintervals, x