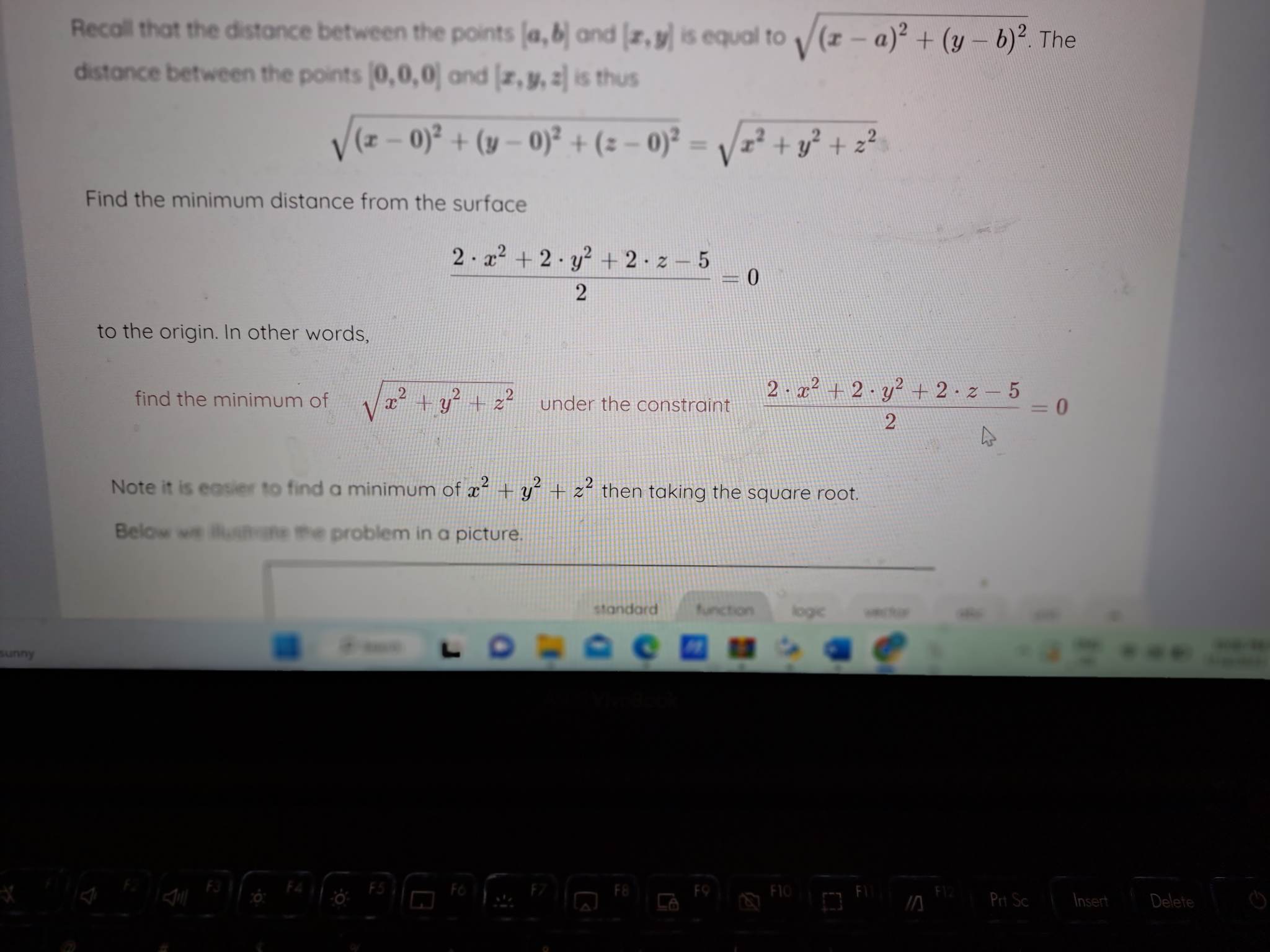
Question: Recall that the distance between the points (a, b) and [z, y) is equal to (x - a)? + (y - b)?. The distance between
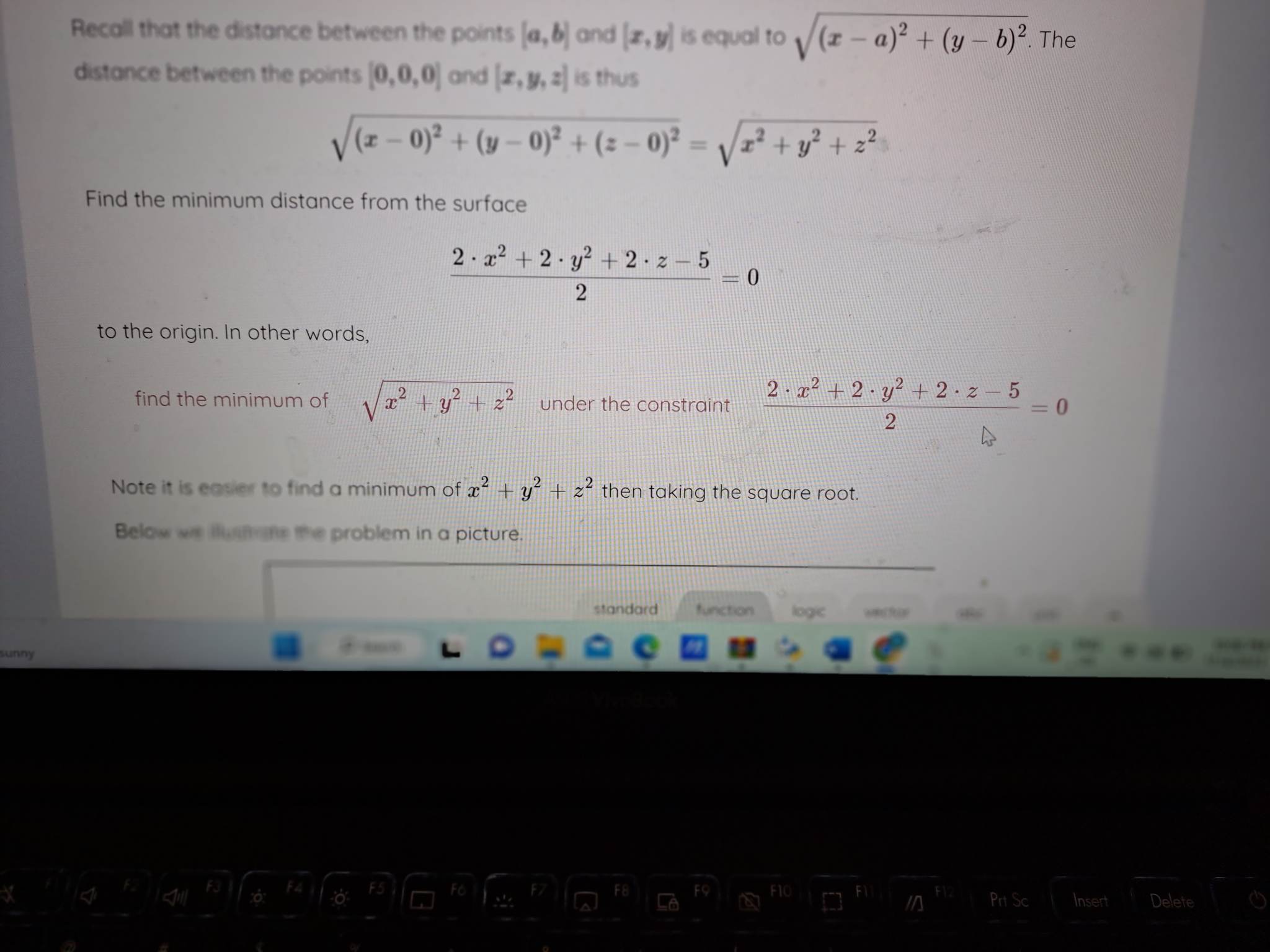
![distance between the points (0,0,0) and [x, y, a] is thus V(z](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6666979354962_507666697932e15f.jpg)
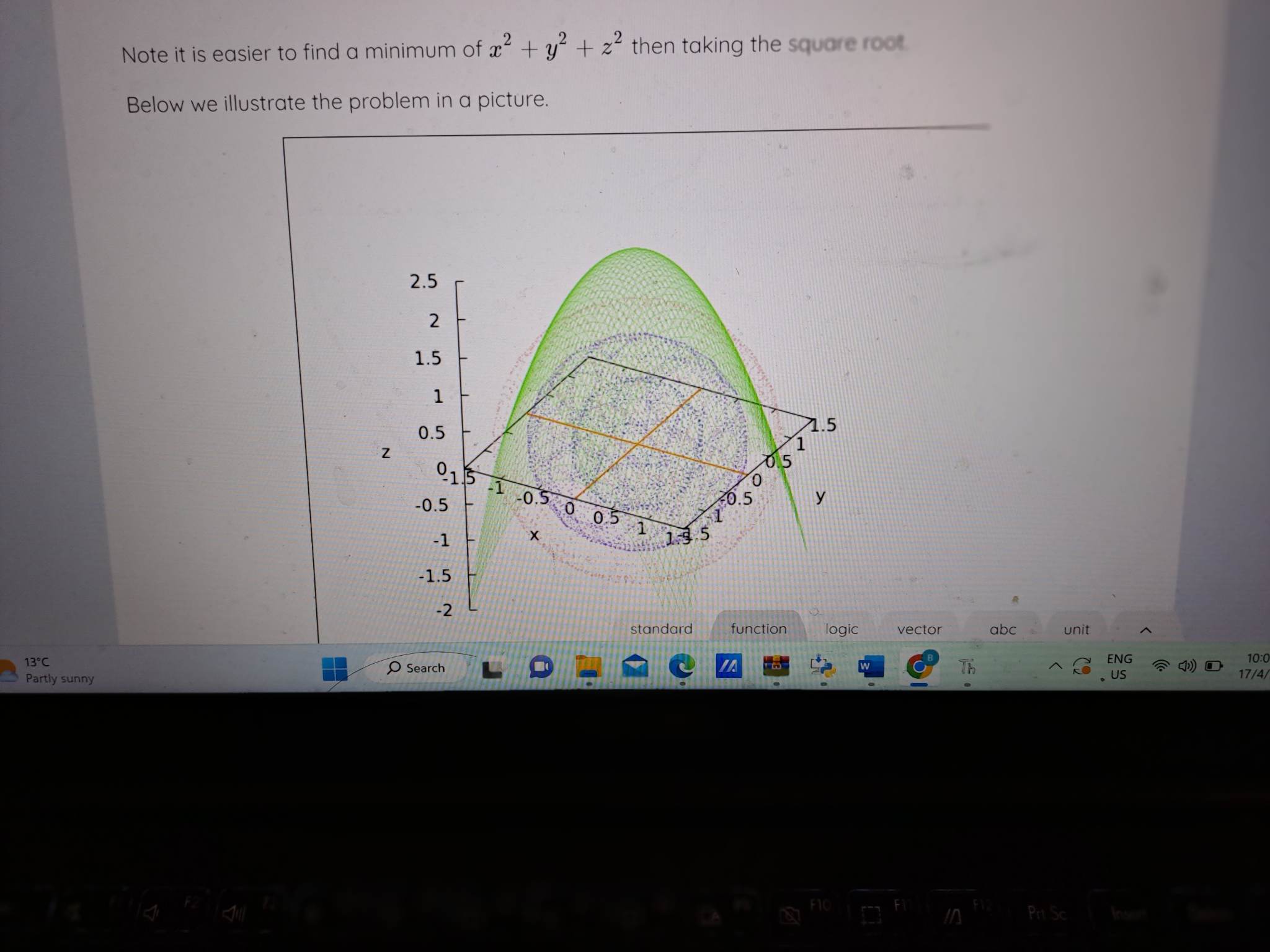
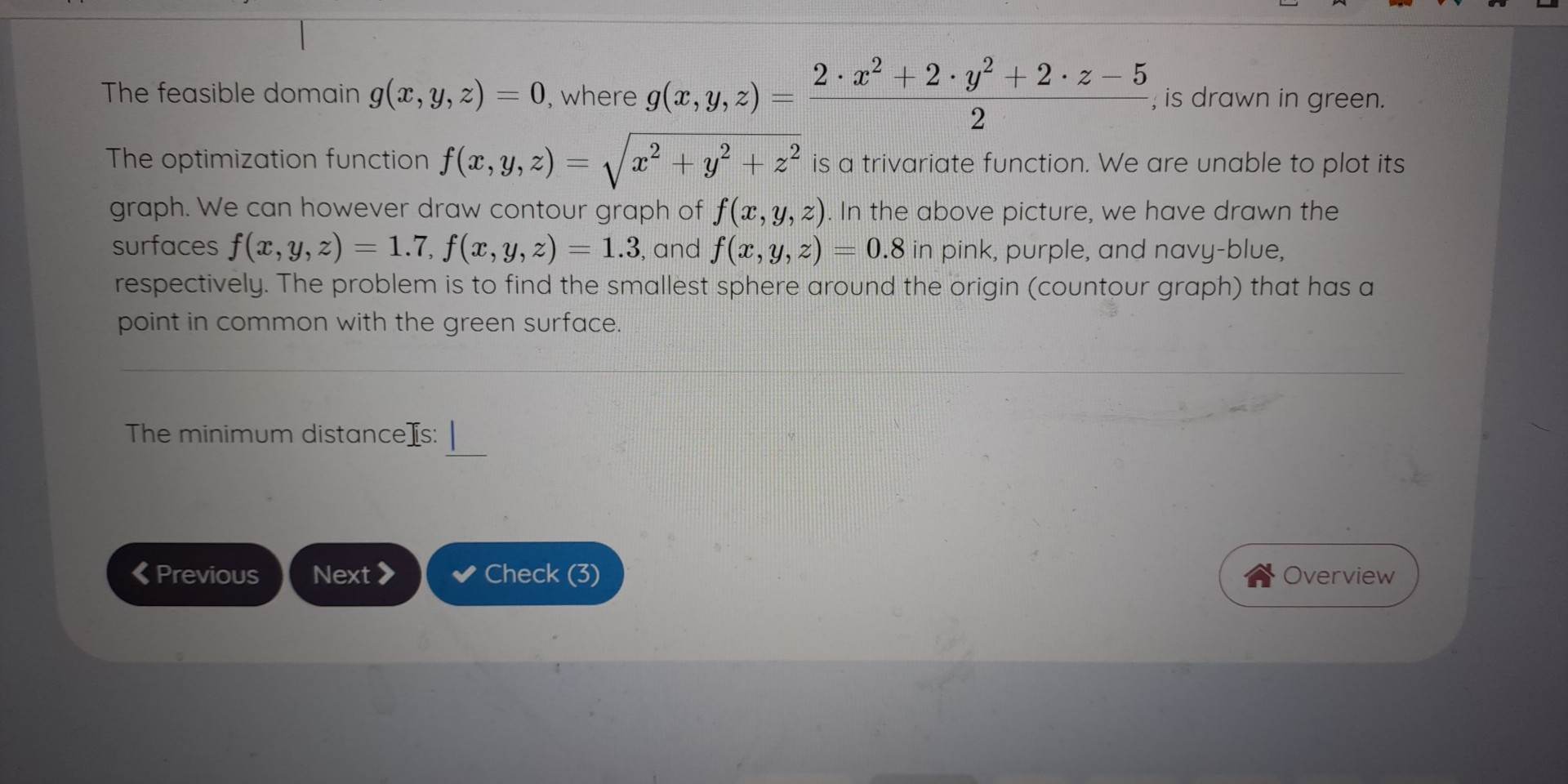
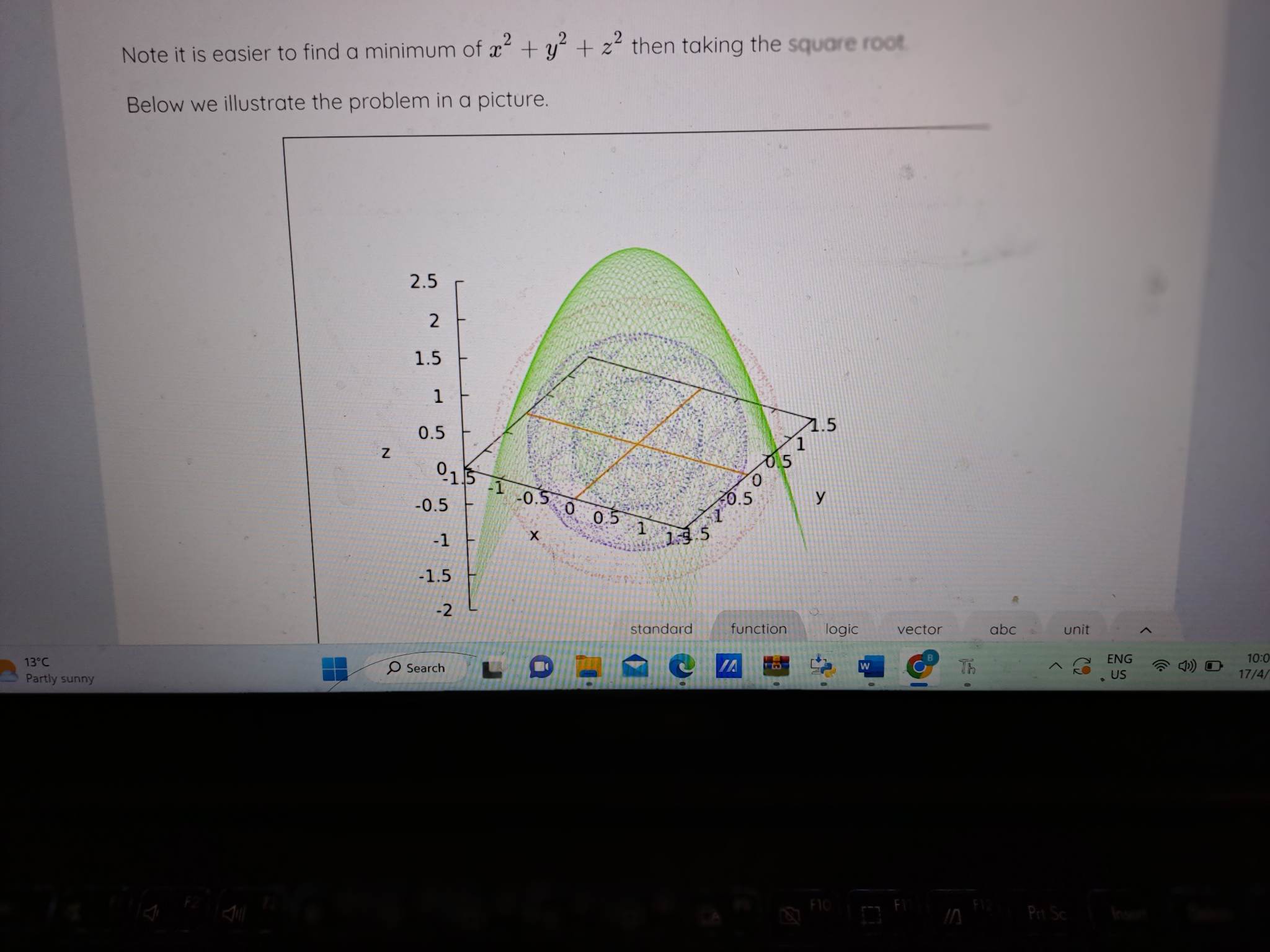
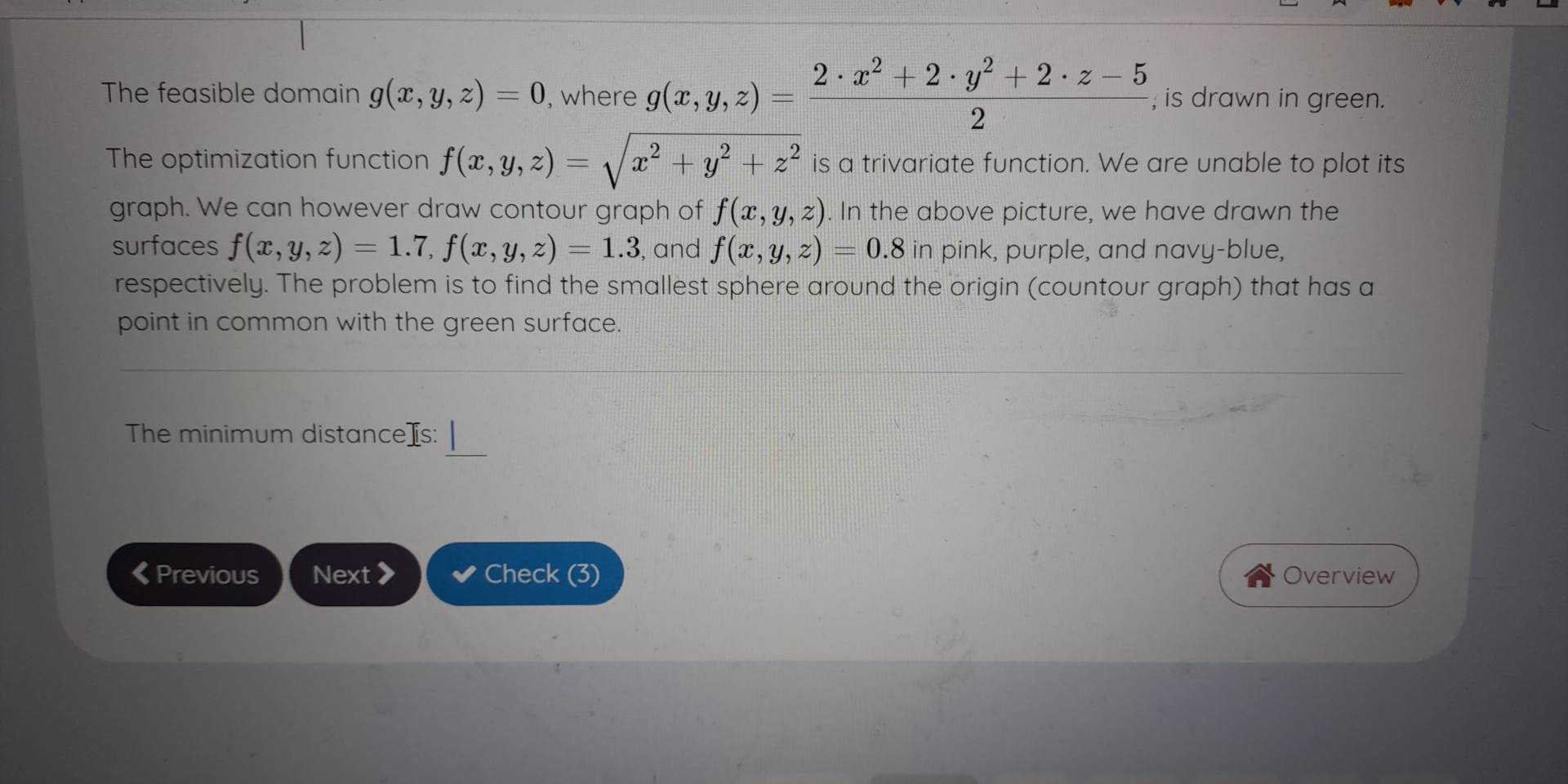
Recall that the distance between the points (a, b) and [z, y) is equal to (x - a)? + (y - b)?. The distance between the points (0,0,0) and [x, y, a] is thus V(z -0)2 + (1-0)3 + (=-0)?=1/12+32+22 Find the minimum distance from the surface 2 . x2 + 2 . y + 2 - 2 -5 0 2 to the origin. In other words, find the minimum of Vx' + y" + 2" under the constraint 2 - 37+ 2- 32 + 2- 2- 5 = 0 2 Note it is easier to find a minimum of a? + y' + 27 then taking the square root. Below we Mightfine the problem in a picture. standard function logs LD FAC M F4 F5 FO FZ F8 FO FIC FI LA Pri Sc Insert DeleteThe feasible domain g(x, y, z) = 0, where g(x, y, z) 2 - 202 + 2 . 32 + 2. 2-5 is drawn in green. 2 The optimization function f(x, y, z) = Vaz + y + 2" is a trivariate function. We are unable to plot its graph. We can however draw contour graph of f(x, y, z). In the above picture, we have drawn the surfaces f(x, y, z) = 1.7, f(x, y, z) = 1.3, and f(x, y, z) = 0.8 in pink, purple, and navy-blue, respectively. The problem is to find the smallest sphere around the origin (countour graph) that has a point in common with the green surface. The minimum distancelis: | Check (3) OverviewThe feasible domain g(x, y, z) = 0, where g(x, y, z) 2 - 202 + 2 . 32 + 2. 2-5 is drawn in green. 2 The optimization function f(x, y, z) = Vaz + y + 2" is a trivariate function. We are unable to plot its graph. We can however draw contour graph of f(x, y, z). In the above picture, we have drawn the surfaces f(x, y, z) = 1.7, f(x, y, z) = 1.3, and f(x, y, z) = 0.8 in pink, purple, and navy-blue, respectively. The problem is to find the smallest sphere around the origin (countour graph) that has a point in common with the green surface. The minimum distancelis: | Check (3) OverviewNote it is easier to find a minimum of a + y + 2 then taking the square root Below we illustrate the problem in a picture. 2.5 N 1.5 0.5 2 15 -0.5 015 -1 0.5 0 05 -1 X -1.5 -2 standard function logic vector abc unit 13.C Partly sunny Search Th ~ KO ENG 10: . US 17/4/ F10 70 Pri SC
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


