Question: Recall that when Sm denotes the n-interval approximation for I = .b [ f ( x ) a whenever L | f (4) (x)|

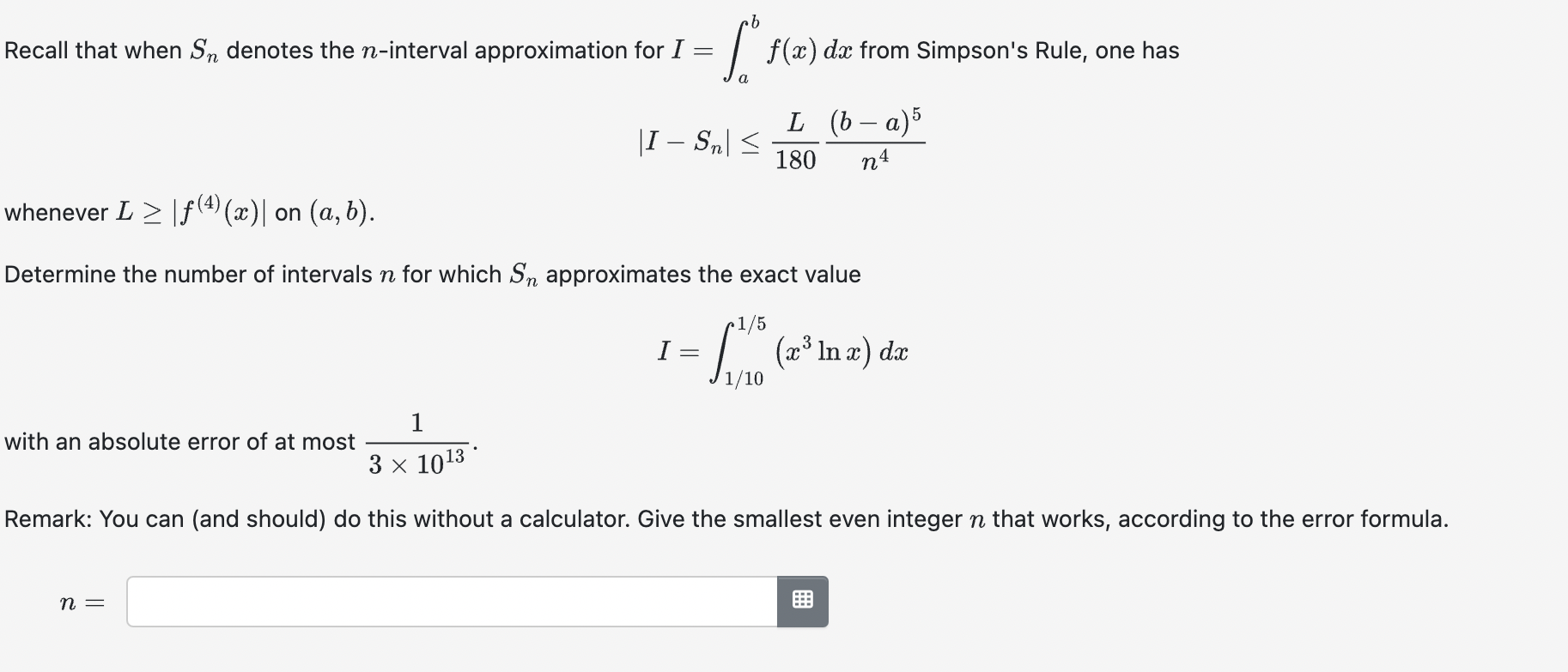
Recall that when Sm denotes the n-interval approximation for I = .b [ f ( x ) a whenever L | f (4) (x)| on (a,b). dx from Simpson's Rule, one has L (b-a)5 |I Sn| 180 n4 Determine the number of intervals n for which Sn approximates the exact value 1 with an absolute error of at most 3 1013 1/5 I = 10 (* In x) dx 1/10 Remark: You can (and should) do this without a calculator. Give the smallest even integer n that works, according to the error formula. n =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Intro Consider a project with a 6-year life and no salvage value. The initial cost to set up the project is $100,000. This amount is to be linearly depreciated to zero over the life of the project....

Write a short paragraph of who I am in a one minute self presentation interview in a hospital setting vacancy focusing on post-award financial management, combining finance and accounting background...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

Choose a company or product that you have been noticing or admiring. Develop a plan to advertise this product that involves the United States and at least one other country, and three forms of media....

A commuter airline deliberately overbooks fights, figuring that only 75% of passengers with reservations show up for its fights. It files small propeller planes that carry 20 passengers. (a) In order...

Gentry Wholesalers accepts from Benton Stores a $6,200, 4-month, 9% note dated May 31 in settlement of Bentons overdue account. (a) What is the maturity date of the note? (b) What is the interest...

Why is the work of Jacques Qutelet so important in the history of psychology?

Elon Motors produces electric automobiles. In recent years, they have been making all components of the cars, excluding the batteries for each vehicle. The company's leadership team has been...

Please solve the following recurrences. Use the Master Theorem whenever possible. ( a ) Tpnq 2 Tp n 4 q 1 . ( b ) Tpnq 2 Tp n 4 q ? n . ( c ) Tpnq 2 Tp n 4 q n . ( d ) Tpnq 2 Tp n 4 q n 2 . ( e )...

During the next 12 months, the amounts of electric power needed (in thousands of kwh) are listed in the file P08_33.xlsx. This power can be supplied using four generators. The generating capacity (in...

Perpetual Inventory Using FIFO Beginning inventory, purchases, and sales for Item Zeta9 are as follows: Oct. 1 Inventory 63 units @ $21 7 Sale 50 units 15 Purchase 71 units @ $24 24 Sale 20 units...

A member tells you that she was recently hospitalized. She received a bill from a collection agency, even though she did not receive a bill from the hospital. She is worried this will affect her...

Boeing's recent results highlighted the case for the stock but perhaps not in the way many investors might think. In truth, they were mixed. However, Boeing's management has conservatively guided...

Two dietary drinks are used to supply protein, carbohydrates, and vitamin C. The first drink provides 2 units of protein, 5 units of carbohydrates, and 7 units of vitamin C in each liter. The second...

5. [9 points] (Mixture Distributions) Consider two continuous random variables Y and Z, and a random variable X that is equal to Y with probability p and Z with probability 1 - p. (One way to think...

Briefly explain how (1) super refraction, (2) subrefraction and (3) ducts could affect the range of a communication link in V/UHF between a ground station and a flying UAV.

Dagger Corporation uses direct labor-hours in its predetermined overhead rate. At the beginning of the year, the total estimated manufacturing overhead was $218.700. At the end of the year, actual...

Why do bars offer free peanuts?

1. Does a company that has no business dealings outside Canada need to concern itself with intercultural communication issues? Explain your answer.

2. What are some intercultural communication issues to consider when deciding whether to accept an overseas job with a firm whose headquarters are in your own country? A job in your own country with...

4. In addition to contextual differences, what other categories of cultural differences exist?