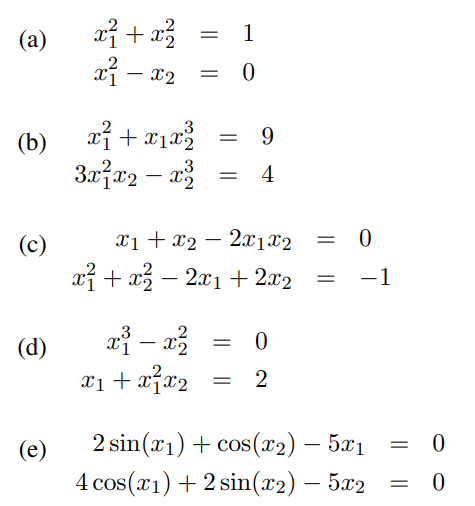
Recall the full-Newton algorithm for solving the nonlinear system F(x) = 0; F, x ERN: Generate an initial approximation o. for k = 0,1, ... until convergence compute - Fik) compute OF (@k) ac solve Fix) Ak = -F(@k) update k+1 = k + Ak end for Implement this algorithm in MatLab. Your function header is function [x, flag] = newt (F, Fprime, n, x0, tol) where F is a vector-valued function which takes as input x ER" and returns F(x) ER", Fprime is a matrix-valued function which takes as input x ER" and returns the Jacobian of aFx) crnxn. F evaluated at x, C, ac n is the dimension of x and F, x0 is an initial approximate solution for F(x) = 0, tol is the required accuracy in the final approximate solution (see below), x is the final approximate solution, and flag is an integer giving the status of the final approximate solution (see below). Convergence is achieved when one or both of the following tests is satisfied: || Tk Xk1 ||2