Question: Recall we define SXT = {(s, t): sS and t T}. For each of the following, prove it if it is always true, else

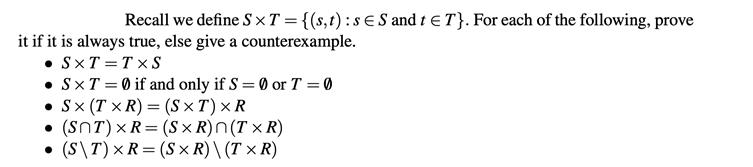
Recall we define SXT = {(s, t): sS and t T}. For each of the following, prove it if it is always true, else

Recall we define SXT = {(s, t): sS and t T}. For each of the following, prove it if it is always true, else give a counterexample. SXT=TXS SXT = 0 if and only if S = 0 or T = 0 Sx (TxR) = (SxT) XR (SNT) XR=(SXR)n(TXR) (S\T) XR=(SXR)\ (TxR)

Step by Step Solution

★★★★★

3.41 Rating (151 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Answer To prove or disprove the statements lets define sets S T and R and examine each case separately 1 SXT TXS To prove this statement we need to show that for any sets S and T the set SXT is equal ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Give the molecular formula for each of the following structural formulas. a. b. c. d. H-N-N-H hydrazine H-o-o-H hydrogen peroxide H-C-C-C-H H O H isopropyl alcohol Cl CI- P CI phosphorus trichloride

Give names for each of the following bicyclic alkanes: (a) (b) (c) (d) (e) (f) Write the structure of a bicyclic compound that is a constitutional isomer of bicyclo[2.2.0]hexane and give its name. CI...

Give an explanation for each of the following facts. (a) Cis- and trans-1.3-dimethylpyrrolidine rapidly interconvert. (b) The following compound exists as the enamine isomer shown rather than as an...

Safety Circuits Inc. is considering investing in a scanner such that they can move from an (R, S) to an (s, Q) inventory policy (see Problem 6.15). It is expected that with a continuous- review...

Please use C++ for this program. Please read the problem and follow the instruction in main.cpp for this program. Problem: - Design an abstract class called Shape: - Private variables double x and...

An ASTM cast iron has minimum ultimate strengths of 30 kpsi in tension and 100 kpsi in compression. Find the factors of safety using the MNS, BCM, and MM theories for each of the following stress...

Give the initial state, goal test, successor function, and cost function for each of the following. Choose a formulation that is precise enough to be implemented. a. You have to color a planar map...

Suppose that you have used the parks-McClellan algorithm to design a causal FIR linear-phase system. The system function of this system is denoted H(z). The length of the impulse response is 25...

In a hypothetical Linux system, each virtual address is 32 bits with a 10-bit page size, 256-entry page table, 32l-entray page middle directory, and 256-entry page directory. Using the Linux model...

As discussed in the All About You feature in this chapter (p. 25), some people are tempted to make their finances look worse to get financial aid. Companies sometimes also manage their financial...

Lois works for Jefferson Movers in Alberta and earns an annual salary of $51,258.00 paid on a semi-monthly basis. She contributes 3% of her gross earnings to a Registered Retirement Savings Plan each...

Listed below are audit situations that may affect the audit of receivables and revenue. a. The audit of a machinery manufacturing company that engages in bill and hold transactions. b. The audit of a...

Calculate the derivative of the following function y = e 5 x ( 5 x 6 ) 4 d y d x =

Supply Ltd entered into a non-cancellable five-year lease arrangement with Customer Ltd on 1 July 2019. The lease is for an item of machinery. There are to be five annual payments of $315 000, the...

Discuss the possible reason why natural radiation dose may vary from region to region.

Q1. Use time and Laplace domain analysis to solve the following differential equation: (10+10) 29(t) + q(t) = 5t q(0) = 5 The table for particular solution is given below: Form of f(t) K Kt K1 K, cos...

Below is the floor plan of the house of the mouse called King, where the rooms and the doors between the rooms are shown. The house is split into 7 rooms, and the passages represent the doors. +- (a)...

Tessa files a Chapter 7 bankruptcy petition. One of Tessa's debts eligible for discharge is a $2000 medical bill that Tessa owes to her physician, Dr. Walker. Tessa trusts Dr. Walker and wants to...

: (i) What data structures are maintained by the page manager. (ii) What happens when a machine performs a read operation to a page. (iii) What happens when a machine performs a write operation to a...

llustrate different ways of connecting these components together to span a range of performance requirements. [10 marks] For each of the performance categories that you identify state today's typical...

You have been provided with the description of a programming language, J, intended for scripting applications. Its syntax is similar to a cut-down version of Java in that it consists of function...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

do the following,..... Write program that reads a person's first and last names, separated by a space. Then the program outputs last name, comma, first name. Create program that takes in user input...

answer the question clearly Describe and compare the call-by-value, call-by-name, and call-by-need evaluation strategies for functional programming languages. The ML function butlast removes the last...