Recursion algrorithem

I am solving this problem using Python, and I don't really know how to do the second question!!!! I have my code at the bottom, please continue with my code and solve question 2(if possible, question3 as well)!!! Thx!!!!

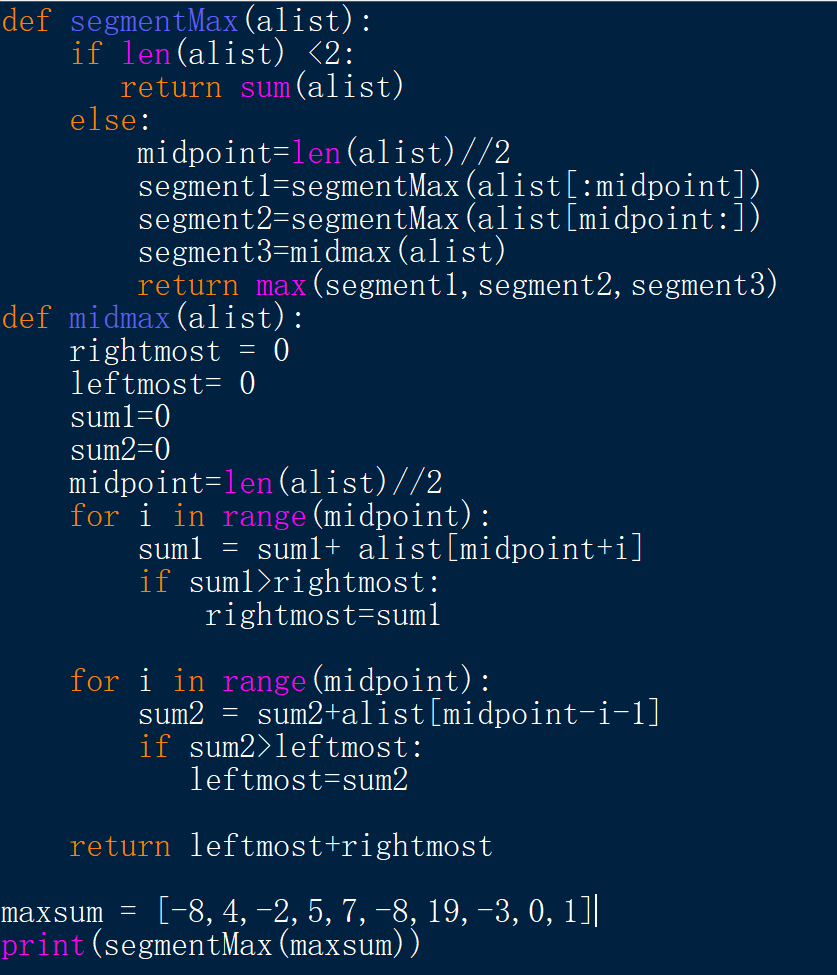
def segmentMax(alist): if len(alist) rightmost: rightmost=sum1 for i in range(midpoint): sum2 = sum2+alist[midpoint-i-1] if sum2>leftmost: leftmost=sum2 return leftmost+rightmost

maxsum = [-8,4,-2,5,7,-8,19,-3,0,1] print(segmentMax(maxsum))

Lab exercises 2 Must be uploaded just after the end of your lab in Week 3 This lab involves developing some divide and conquer algorithms, to solve the maximum segment sum problerm Suppose you are given a list of integers (so some might be negative). The maximum segment sum of the list is the contiguous sublist whose sum is the largest. (Note that there's an ambiguity if there are Os in the list; these are not usually counted in the maximum segment, so we're actually looking for the shortest sequence with the largest sum For example if the list is [2 45 -7 3-614], then the maximum segment sum is 11 and the corresponding segment is [2 4 5]. Notice that negative numbers don't necessary act as stoppers to maximum segments if the sums orn both sides are large There's an obvious O(n 2) algorithm: check the segment sum between every possible start and end position. But the goal is to develop a divide and conquer algorithm As usual, we will divide the list in half recursively; and the base case will be the segment sum of whatever short sequence you choose to stop at. But the key insight is that, if every recursive call returns information about the maximum segment sum it contains and the maximum sums that end at its right and left ends, then these results from the two children can be assembled into the same information to pass upwards. At the top level of the recursion, the contained maximum segment sum is the desired answer. (This should remind you of the maximum path in an unrooted tree problem, but in this case each recursive call can't tell if it's a left or a right child of its parent and so has to keep track of the segments that end at both left and right.) 1. Build an implementation of mss using this strategy. So that you can't just copy one of the many thousands of implementations from the Web, let's solve this specialised version: given a list of integers whose length is n compute the maximum segment sum and the elements of the maximum segment between given positions left