Recursion approach. It is also possible to implement, DFS using recursion:

Initialization before recursion: All nodes are labeled not visited.

procedure DFS-recursive(v): label v as visited for all nodes w adjacent to v in increasing order of w do if w is not visited then call DFS-recursive(w)

smallgraph.txt

6 100 -10 15 -50 -60 70 -30 0 1 1 2 1 3 3 4 4 5

// graph.h

#ifndef Graph_h #define Graph_h

#pragma once

#include using namespace std;

class Graph { public: Graph(); // default constructor Graph(int rno, float rbudget); // constructor with two arguments representing the number of nodes, initial budget void addEdge(int node1, int node2); // adds an edge between two nodes in the graph node1 and node2 //void setValue(int node, float rval); // sets a value for a node void setBudget(float rbu); // sets the initial budget int getNSize(); // return number of nodes int getESize(); // return number of edges float getBudget(); // return current budget //float getValue(int node); // returns the value of the node

private: // member variables and helper functions (if needed) };

#endif

//graph.cpp

#include "graph.h"

// TO BE COMPLETED WITH IMPLEMENTATIONS OF GRAPH MEMBER FUNCTIONS Graph::Graph(){}

Graph::Graph(int rno, float rbudget){}

void Graph::addEdge(int node1, int node2){}

void Graph::setValue(int node, float rval){}

void Graph::setBudget(float rbu){}

int Graph::getNSize(){}

int Graph::getESize(){}

float Graph::getBudget(){}

float Graph::getValue(int node){}

//main.cpp

#include #include #include #include #include

#include "Graph.h"

using namespace std;

////////////////////////////////////////////////////////////////////////////// // DO NOT EDIT THIS FILE (except for your own testing) // CODE WILL BE GRADED USING A MAIN FUNCTION SIMILAR TO THIS //////////////////////////////////////////////////////////////////////////////

template bool testAnswer(const string &nameOfTest, const T& received, const T& expected) { if (received == expected) { cout

template bool testArrays(const string& nameOfTest, const T& received, const T& expected, const int& size) { for (int i = 0; i

cout

int main() {

Graph testGraph01(3, 100.0); testAnswer("testGraph01.getNSize()", testGraph01.getNSize(), 3); testAnswer("testGraph01.getESize()", testGraph01.getESize(), 0); testAnswer("testGraph01.getBudget()", testGraph01.getBudget(), (float)100.0);

// add edges to testGraph01 and test testGraph01.addEdge(0, 1); testGraph01.addEdge(0, 2); testAnswer("testGraph01.getESize()", testGraph01.getESize(), 2); // add values to testGraph01 and test testGraph01.setValue(0, -50.0); testGraph01.setValue(1, -60.0); testGraph01.setValue(2, -70.0); testAnswer("testGraph01.getValue(0)", testGraph01.getValue(0), (float)-50.0); testAnswer("testGraph01.getValue(2)", testGraph01.getValue(2), (float)-70.0);

system("pause"); return 0; }

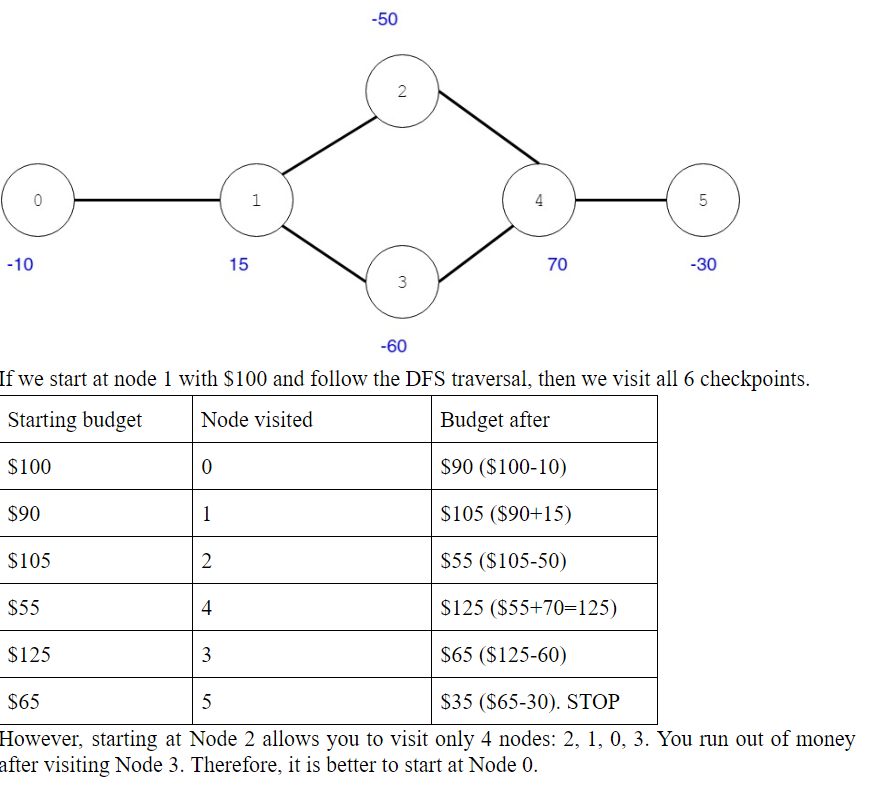
A graph G-(V,E) is simply a set of vertices V, and a set of edges E between those vertices. It may be more convenient to think about a graph as being a network. We consider a maze in which the nodes represent checkpoints and the edges represent the pathways between the points. Each checkpoint hides a value, that can be positive or negative. The value does not change and can be collected only once, irrespective of how many times you go through that checkpoint. Let us say that you start with $100 in your wallet, and you go from one check point to another. If the value is positive, it is added to your wallet. If it is negative, it is deducted from your wallet. You can keep going as long as you have a positive value left in your wallet. The goal is to visit as many checkpoints as you can during a DFS traversal. The only choice you have is where to start. Game Collection We consider an undirected graph. Let?n represent the number of nodes. For simplicity, we label the nodes in increasing order from ?0, 1, ..., n-1?. Given an undirected graph, a value for each node, a starting point and a startup budget, find the node that maximizes the number of checkpoints visited during a DFS: Input?: ?n?, ?starting budget?, ?values: ?an array of ?n? values, ? ?and an array o edges. Output?: the node that maximizes the number of checkpoints visited during a DFS. DFS Traversal There are two approaches to implementing DFS. You need to pick only one. ?For this project, your DFS traversal should stop if the budget is negative Need help with the only ones given here is the code A graph G-(V,E) is simply a set of vertices V, and a set of edges E between those vertices. It may be more convenient to think about a graph as being a network. We consider a maze in which the nodes represent checkpoints and the edges represent the pathways between the points. Each checkpoint hides a value, that can be positive or negative. The value does not change and can be collected only once, irrespective of how many times you go through that checkpoint. Let us say that you start with $100 in your wallet, and you go from one check point to another. If the value is positive, it is added to your wallet. If it is negative, it is deducted from your wallet. You can keep going as long as you have a positive value left in your wallet. The goal is to visit as many checkpoints as you can during a DFS traversal. The only choice you have is where to start. Game Collection We consider an undirected graph. Let?n represent the number of nodes. For simplicity, we label the nodes in increasing order from ?0, 1, ..., n-1?. Given an undirected graph, a value for each node, a starting point and a startup budget, find the node that maximizes the number of checkpoints visited during a DFS: Input?: ?n?, ?starting budget?, ?values: ?an array of ?n? values, ? ?and an array o edges. Output?: the node that maximizes the number of checkpoints visited during a DFS. DFS Traversal There are two approaches to implementing DFS. You need to pick only one. ?For this project, your DFS traversal should stop if the budget is negative Need help with the only ones given here is the code