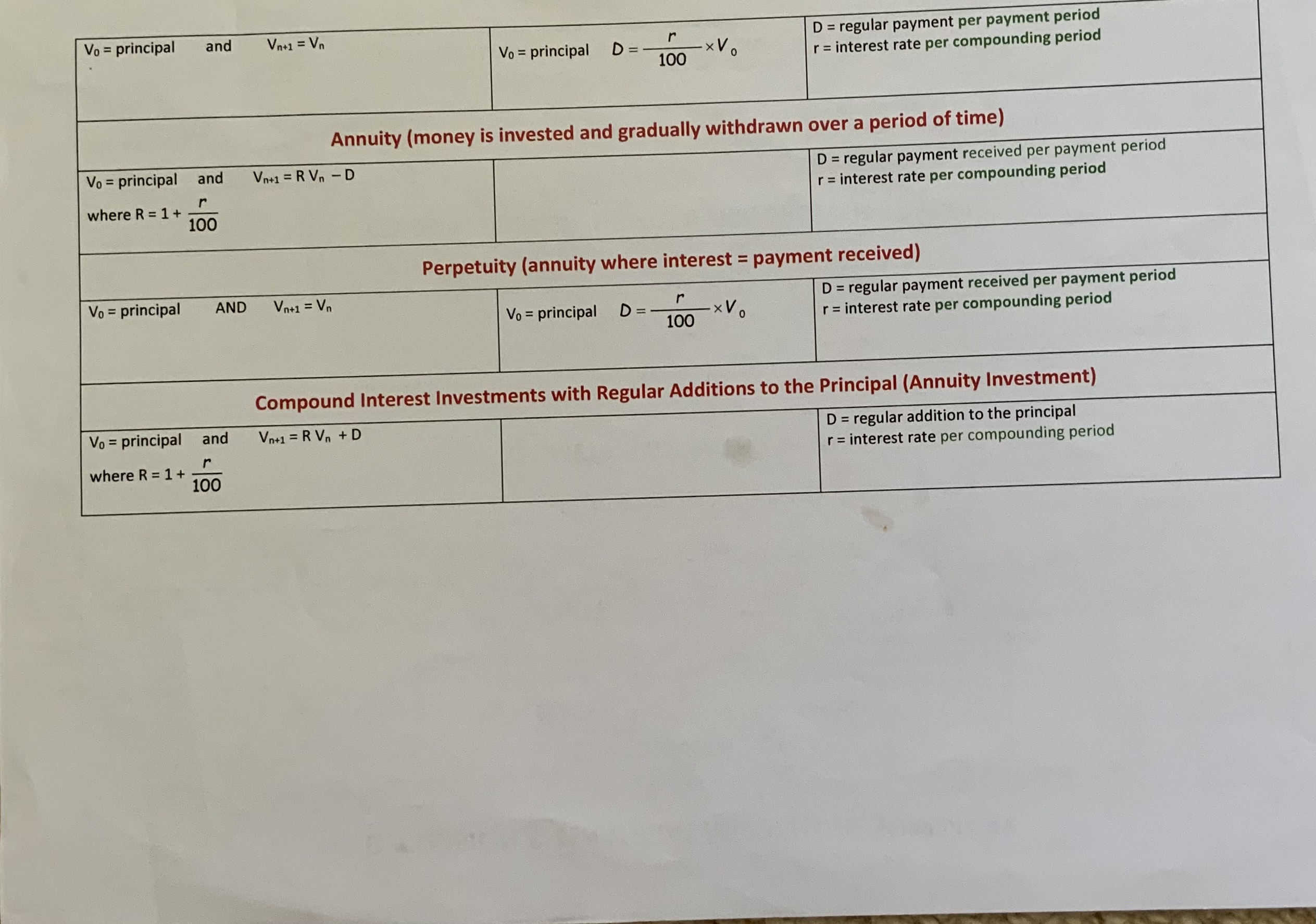
Question: RECURSION & FINANCIAL MODELLING SUMMARY Recurrence Relation Rule Notes LINEAR GROWTH / DECAY A. Simple Interest Loans / Investments Vo = principal AND Vn+1 =



Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


